Содержание
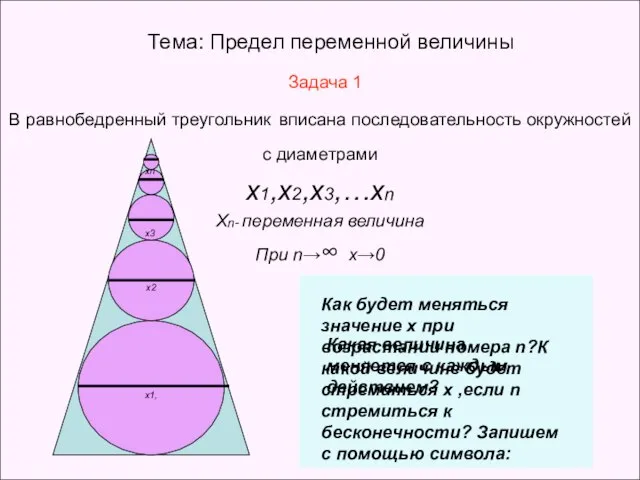
- 2. Тема: Предел переменной величины Задача 1 В равнобедренный треугольник вписана последовательность окружностей с диаметрами х1,х2,х3,…хn Хn-
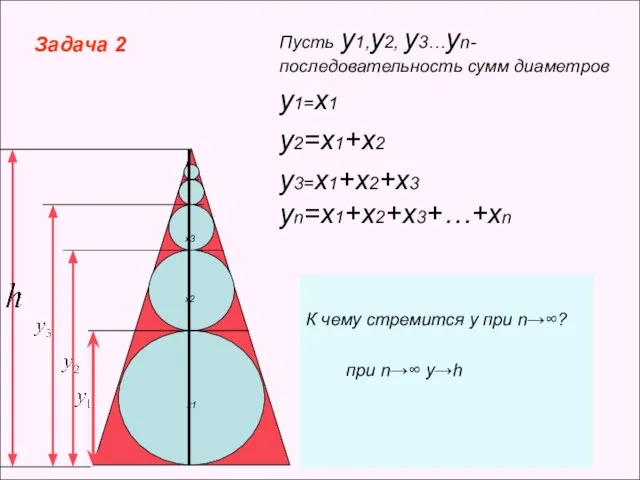
- 3. х1 х2 х3 Пусть у1,у2, у3…уn- последовательность сумм диаметров у1=х1 у2=х1+х2 у3=х1+х2+х3 уn=х1+х2+х3+…+хn К чему стремится
- 4. определение Число а есть предел переменной величины х, если в процессе своего изменения х неограниченно приближается
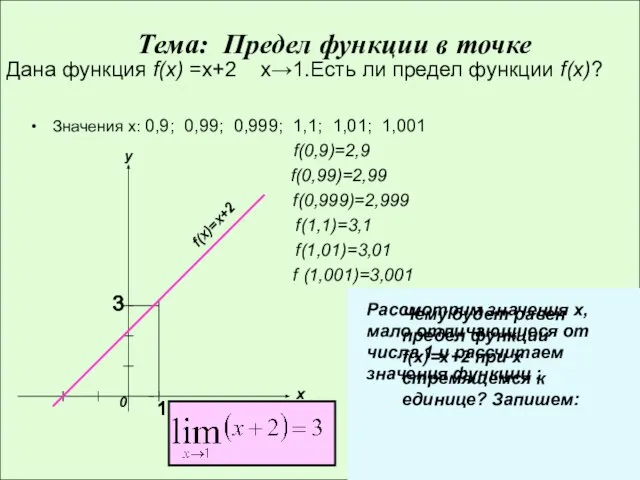
- 5. Дана функция f(x) =х+2 х→1.Есть ли предел функции f(x)? Значения х: 0,9; 0,99; 0,999; 1,1; 1,01;
- 7. Скачать презентацию

 Спасо-Преображенский собор (г. Переславль-Залесский. Храмы Золотого кольца России)
Спасо-Преображенский собор (г. Переславль-Залесский. Храмы Золотого кольца России) Презентация на тему Скорость. Время. Расстояние 3 класс
Презентация на тему Скорость. Время. Расстояние 3 класс Род несклоняемых существительных (5 класс)
Род несклоняемых существительных (5 класс) Промышленные подходы привлечения поискового трафика
Промышленные подходы привлечения поискового трафика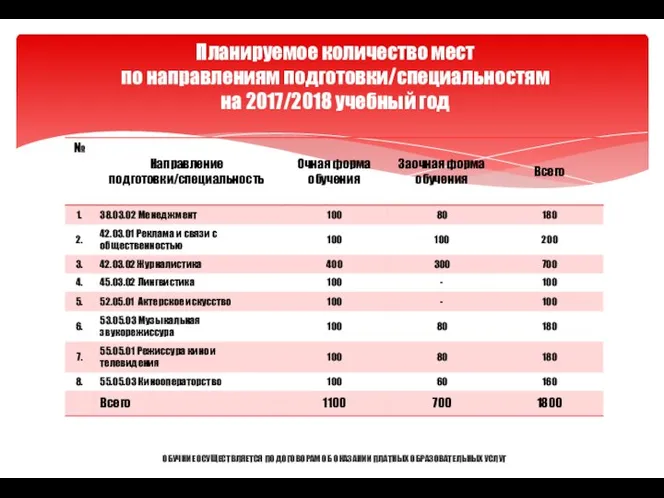 Планируемое количество мест по направлениям подготовки/специальностям на 2017/2018 учебный год
Планируемое количество мест по направлениям подготовки/специальностям на 2017/2018 учебный год Imperfectum indicativi activi et passivi (прошедшее время несовершенного вида изъявительного наклонения )
Imperfectum indicativi activi et passivi (прошедшее время несовершенного вида изъявительного наклонения ) Пример портфолио
Пример портфолио Учебные мотивы на разных этапах онтогенеза.
Учебные мотивы на разных этапах онтогенеза. 5 октября празднуется Всемирный ДЕНЬ УЧИТЕЛЯ! И мы, ученики 3 «Б» класса лицея № 6 г. Бердска, подготовили поздравления для наш
5 октября празднуется Всемирный ДЕНЬ УЧИТЕЛЯ! И мы, ученики 3 «Б» класса лицея № 6 г. Бердска, подготовили поздравления для наш Информационная бизнес-платформа InterKent
Информационная бизнес-платформа InterKent Книги, которые нужно прочитать до 25 лет
Книги, которые нужно прочитать до 25 лет «ЧТОБЫ ЗНАЛИ И ПОМНИЛИ !»
«ЧТОБЫ ЗНАЛИ И ПОМНИЛИ !» ехали, ехали
ехали, ехали Famous people o Great Britain
Famous people o Great Britain Этапы разработки и исследования моделей на компьютере
Этапы разработки и исследования моделей на компьютере 20161210_9_klass_ugolnaya_prom
20161210_9_klass_ugolnaya_prom Каранин
Каранин Михаил Александрович Шолохов
Михаил Александрович Шолохов Деловой этикет. Лекция 8
Деловой этикет. Лекция 8 Элементы фирменного стиля предприятия
Элементы фирменного стиля предприятия Электрические машины
Электрические машины Правила безопасного поведения во время зимних каникул
Правила безопасного поведения во время зимних каникул Валы и оси
Валы и оси Квиллинг
Квиллинг Элетронная таблица Excel
Элетронная таблица Excel Рождество в неоновом свете
Рождество в неоновом свете Презентация V.I.C.
Презентация V.I.C. Основные глобальные проблемы пленеты Земля
Основные глобальные проблемы пленеты Земля