Слайд 21. Понятие предиката
Логика предикатов расчленяет элементарное высказывание на субъект (буквально

— подлежащее, хотя оно и может играть роль дополнения) и предикат (буквально - сказуемое, хотя оно может играть и роль определения).
Слайд 3 Субъект — это то, о чем что-то утверждается в высказывании; предикат

- это то, что утверждается о субъекте.
Слайд 4Пример:
В высказывании «7 - простое число», «7» -субъект, «простое число» - предикат.

Это высказывание утверждает, что «7» обладает свойством «быть простым числом».
Если в рассмотренном примере заменить конкретное число 7 переменной х из множества натуральных чисел, то получим высказывательную форму «х - простое число». При одних значениях х, (например, х = 13, х =17 ) эта форма дает истинные высказывания, а при других значениях х (например, х = 10 , х = 18 ) эта форма дает ложные высказывания.
Слайд 5 Одноместным предикатом Р(х) называется произвольная функция переменного х, определенная на множестве

М и принимающая значения из множества {1,0}.
Слайд 6
Множество М, на котором определен предикат P(х) , называется областью определения

предиката.
Слайд 7 Множество всех элементов х ∈ М , при которых предикат принимает

значение «истина», называется множеством истинности предиката Р(х).
Слайд 8Примеры:
Р(х) - «х - простое число» определен на множестве N, а множество

истинности для него есть множество всех простых чисел.
Предикат Q{x} - « sin х = 0 » определен на множестве R, а его множество истинности -Q.
Предикат F(x) - «Диагонали параллелограмма перпендикулярны» определен на множестве всех параллелограммов, а его множеством истинности является множество всех ромбов.
Слайд 9 Предикат Р(х), определенный на множестве М, называется тождественно истинным ,если область

определения предиката и область истинности совпадают.
Слайд 102. Логические операции над предикатами
Предикаты, так же, как высказывания, принимают два значения

истина и ложь (1, 0), поэтому к ним применимы все операции логики высказываний.
Слайд 11 Конъюнкцией двух предикатов Р(х) и Q(x) называется новый предикат Р(х)Λ Q{x),

который принимает значение «истина» при тех и только тех значениях х ∈ М, при которых каждый из предикатов принимает значение «истина», и принимает значение «ложь» во всех остальных случаях.
Слайд 12Пример:
Для предикатов Р(х): «х – четное число» и Q(x): «х кратно

3» конъюнкцией P(x)ΛQ(x) является предикат «х - четное число и х кратно 3», то есть предикат «х делится на 6»
Слайд 13Дизъюнкцией двух предикатов Р(х) и Q(x) называется новый предикат Р(х)V Q(x), который

принимает значение «ложь» при тех и только тех значениях х ∈ М, при которых каждый из предикатов принимает значение «ложь» и принимает значение «истина» во всех остальных случаях.
Слайд 14 Отрицанием предиката Р(х) называется новый предикат , который принимает значение «истина»

при всех значениях х ∈ М, при которых предикат Р(х) принимает значение «ложь», и принимает значение «ложь» при тех значениях х ∈ М, при которых предикат Р(х) принимает значение «истина».
Слайд 15Задание 1
Для следующих предложений выделить предикаты и для каждого из них

указать область истинности:
х+5=1;
х+2<3x – 4;
однозначное число х кратно 3;














 История создания сети интернет
История создания сети интернет Презентация на тему Русская армия в 18 веке и её великие полководцы
Презентация на тему Русская армия в 18 веке и её великие полководцы Предпринимательство и его организационные формы. Тема 14
Предпринимательство и его организационные формы. Тема 14 Презентация на тему Международные экономические организации Международные правительственные (межгосударственные) экономически
Презентация на тему Международные экономические организации Международные правительственные (межгосударственные) экономически Овощной салат с зелёным чаем
Овощной салат с зелёным чаем Липецкий зоопарк
Липецкий зоопарк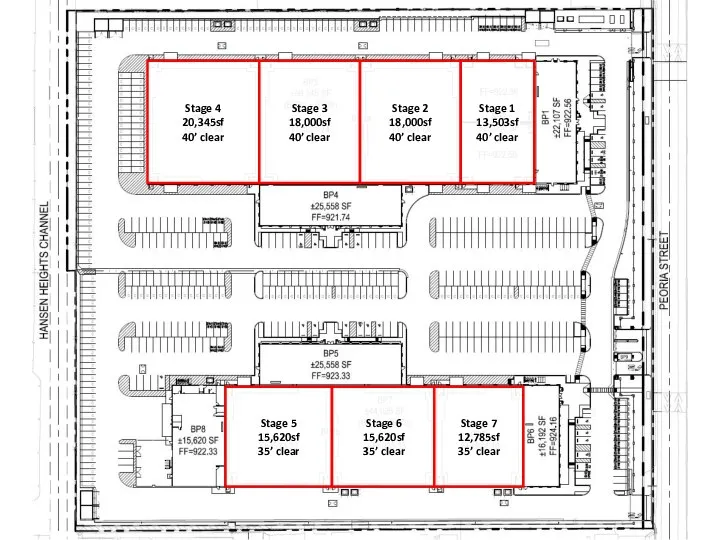 Sun Valley Site Plan Mock Up
Sun Valley Site Plan Mock Up OET-12
OET-12 Отношение студентов ТМК к занятиям спортом в учебное время
Отношение студентов ТМК к занятиям спортом в учебное время Здоровьесберегающие технологии в начальной школе
Здоровьесберегающие технологии в начальной школе Фоносемантический анализ предложения
Фоносемантический анализ предложения Повышение эффективности использования машиннотракторного агрегата для поверхностной обработки
Повышение эффективности использования машиннотракторного агрегата для поверхностной обработки Региональные налоги РФ
Региональные налоги РФ Психология, педагогика және мәдениет факультеті
Психология, педагогика және мәдениет факультеті Создание макета русской деревни в рамках предмета «Технология»
Создание макета русской деревни в рамках предмета «Технология» Единый недвижимый комплекс
Единый недвижимый комплекс Судейский семинар национальной категории по дисциплинам спидскейтинга
Судейский семинар национальной категории по дисциплинам спидскейтинга SFM-285 СПМ200-6843080 “Набивка подушки”. Форма заливочная. Концепт разъема
SFM-285 СПМ200-6843080 “Набивка подушки”. Форма заливочная. Концепт разъема 2022-04-04_GIA-9_normat_dok
2022-04-04_GIA-9_normat_dok Способы формирования познавательного интереса, как необходимого условия повышения качества знаний учащихся
Способы формирования познавательного интереса, как необходимого условия повышения качества знаний учащихся Презентация на тему Агроклиматические ресурсы
Презентация на тему Агроклиматические ресурсы  Підвищення кваліфікації вчителів за напрямом інформатика
Підвищення кваліфікації вчителів за напрямом інформатика Надзвичайні ситуації та їх запобігання
Надзвичайні ситуації та їх запобігання Жизненный и творческий путь Александра Блока
Жизненный и творческий путь Александра Блока Ораторское искусство
Ораторское искусство Айфоны X, XR и XS MAX
Айфоны X, XR и XS MAX ЕГЭ ПО РУССКОМУ ЯЗЫКУ2011
ЕГЭ ПО РУССКОМУ ЯЗЫКУ2011 Проектная работа «Кулинарная книга 1 – В класса».
Проектная работа «Кулинарная книга 1 – В класса».