Содержание
- 2. Единицы измерения информации Единица информации называется битом. Термин "бит" предложен как аббревиатура от английского словосочетания "Binary
- 3. Единицы измерения информации В информатике часто используется величина, называемая байтом (byte) и равная 8 битам. И
- 4. Представление числовой информации Числовая информация была первым видом информации, который начали обрабатывать ЭВМ, и долгое время
- 5. Беззнаковые целые числа Беззнаковые целые числа представляются в машине наиболее просто. Для этого достаточно перевести требуемое
- 6. Переполнение Если теперь внимательно посмотреть на полученные результаты, то можно заметить, что при последовательном увеличении на
- 7. Целые числа со знаком Для того, чтобы различать положительные и отрицательные числа, в двоичном представлении чисел
- 8. Дополнительный код числа В его основе лежит запись отрицательных чисел в виде 2N - |m|, где
- 9. Представление вещественных чисел Принципиальное отличие между вещественными и целыми числами: целые числа дискретны, и отсюда (если
- 10. Представление с плавающей запятой любое число A в системе счисления с основанием Q можно записать в
- 11. Представление с плавающей запятой Все сказанное о нормализации можно применять и к двоичной системе: A =
- 12. Представление с плавающей запятой при использовании метода представления вещественных чисел с плавающей запятой фактически хранится два
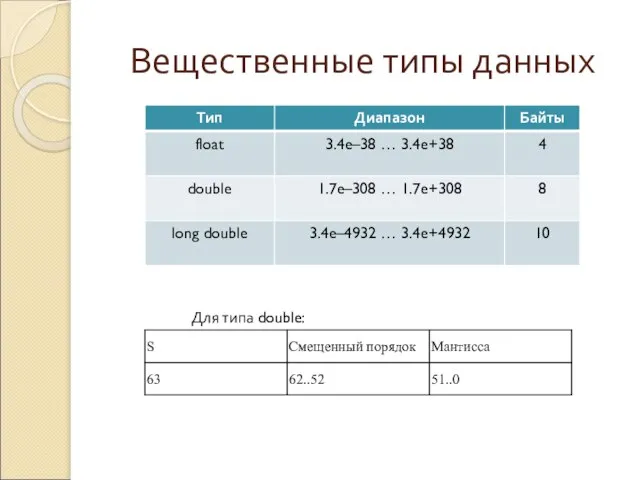
- 13. Вещественные типы данных Для типа double:
- 14. Представление чисел с плавающей запятой Для упрощения вычислений и сравнения действительных чисел значение порядка в ЭВМ
- 15. Пример: Запишем код числа -312,3125. Двоичная запись модуля этого числа имеет вид 100111000,0101. Проведем нормализацию, получим
- 16. Обратный переход от кода действительного числа к самому числу Пусть дан код 3FEC600000000000(16) Прежде всего замечаем,
- 17. Представление текстовой информации Текстовая информация, как и любая другая, хранится в памяти компьютера в двоичном виде.
- 18. Таблица ASCII
- 20. Скачать презентацию
Слайд 2Единицы измерения информации
Единица информации называется битом. Термин "бит" предложен как аббревиатура от
Единицы измерения информации
Единица информации называется битом. Термин "бит" предложен как аббревиатура от

В компьютерной технике бит соответствует физическому состоянию носителя информации: намагничено - не намагничено, есть отверстие - нет отверстия. При этом одно состояние принято обозначать цифрой 0, а другое - цифрой 1. Выбор одного из двух возможных вариантов позволяет также различать логические истину и ложь. Последовательностью битов можно закодировать текст, изображение, звук или какую-либо другую информацию. Такой метод представления информации называется двоичным кодированием (binary encoding).
Слайд 3Единицы измерения информации
В информатике часто используется величина, называемая байтом (byte) и равная
Единицы измерения информации
В информатике часто используется величина, называемая байтом (byte) и равная

В большинстве современных ЭВМ при кодировании каждому символу соответствует своя последовательность из восьми нулей и единиц, т. е. байт
Наряду с байтами для измерения количества информации используются более крупные единицы:
1 Кбайт (один килобайт) = 210 байт = 1024 байта; 1 Мбайт (один мегабайт) = 210 Кбайт = 1024 Кбайта = 220 байт; 1 Гбайт (один гигабайт) = 210 Мбайт = 1024 Мбайта = 230 байт.
1 Тбайт (один терабайт) = 210 Гбайт = 1024 Гбайт = 240 байт, 1 Пбайт(один петабайт) = 210 Тбайт = 1024 Тбайт = 250 байт.
Слайд 4Представление числовой информации
Числовая информация была первым видом информации, который начали обрабатывать ЭВМ,
Представление числовой информации
Числовая информация была первым видом информации, который начали обрабатывать ЭВМ,

Слайд 5Беззнаковые целые числа
Беззнаковые целые числа представляются в машине наиболее просто. Для этого
Беззнаковые целые числа
Беззнаковые целые числа представляются в машине наиболее просто. Для этого

Например, восьмиразрядное ( 1 байт) число 14 будет иметь вид 0000 1110. Это же самое число в 16 - разрядном представлении будет иметь слева еще 8 нулей.
Просто определить минимальное и максимальное значение чисел для N-разрядного беззнакового целого: минимальное состоит из одних нулей, а значит, при любом N равняется нулю; максимальное, напротив, образовано одними единицами и, разумеется, для разных N различно. Для вычисления максимально допустимого значения обычно используют формулу: Max = 2N - 1.
Если выполнить следующие операции: 255 + 1 и 0 - 1.
Мысленно представим себе, что при осуществлении операции слева существует еще один дополнительный (девятый) разряд. И , отбросив несуществующий дополнительный разряд, получаем несколько странный, но действительно имеющий место на практике результат: 255 + 1 = 0. А 0-1=255.
Слайд 6Переполнение
Если теперь внимательно посмотреть на полученные результаты, то можно заметить, что при
Переполнение
Если теперь внимательно посмотреть на полученные результаты, то можно заметить, что при

Обсуждаемая проблема выхода за отведенную разрядную сетку машины занимает важное место в реализации компьютерной арифметики и называется переполнением. Ситуация эта не совсем нормальная и для получения достоверных результатов ее следует избегать. Положение осложняется тем, что для процессора описанные результаты не являются чем-то "угрожающим", и он "спокойно" продолжает вычисления. Единственная тонкость заключается в том, что сам факт переполнения всегда фиксируется путем установки в единицу специального управляющего бита, который последующая программа имеет возможность проанализировать. Образно говоря, процессор "замечет" переполнение, но предоставляет программному обеспечению право принять решение реагировать на него или проигнорировать.
Слайд 7Целые числа со знаком
Для того, чтобы различать положительные и отрицательные числа, в
Целые числа со знаком
Для того, чтобы различать положительные и отрицательные числа, в

Представление положительных чисел при переходе от беззнаковых чисел к целым со знаком сохраняется, за исключением того, что теперь для собственно числа остается на один разряд меньше.
Первое, что приходит в голову, это кодировать отрицательные значения точно так же, как и положительные, только добавлять в старший бит единицу. Подобный способ кодирования называется прямым кодом.
Слайд 8Дополнительный код числа
В его основе лежит запись отрицательных чисел в виде 2N
Дополнительный код числа
В его основе лежит запись отрицательных чисел в виде 2N

Однако способ расчета, вытекающий непосредственно из определения, не слишком хорош, поскольку требует от конструкции процессора дополнительного разряда. Поэтому для практического получения кода отрицательных чисел используется следующий эквивалентный алгоритм. Для преобразования отрицательного числа в дополнительный код необходимо:
Модуль числа перевести в двоичную форму.
Проинвертировать каждый разряд получившегося кода, т.е. заменит единицы нулями, а нули – единицами (полученный код называется обратным).
К обратному коду прибавить единицу.
Пример 1: Перевести число – 8 в двоичный 8 - разрядный код.
Возьмем модуль числа (810 = 10002) и дополним его до необходимого числа разрядов нулями слева: 0000 1000.
Теперь проинвертируем: 1111 0111.
Прибавим единицу. Получим окончательный ответ: 11111000
Для проверки правильности перевода можно сложить последнее число с исходным и убедиться в том, что результат будет нулевым (единицей переноса из старшего разряда, как обычно, пренебрегаем).
Проведем сопоставление целых чисел без знака и со знаком. Результат сравнения чисел со знаком и без него состоит в том, что общее количество их значений одинаково, но их диапазоны сдвинуты вдоль числовой оси.
Слайд 9Представление вещественных чисел
Принципиальное отличие между вещественными и целыми числами: целые числа дискретны,
Представление вещественных чисел
Принципиальное отличие между вещественными и целыми числами: целые числа дискретны,

Существует два способа представления вещественных чисел: с фиксированной и с плавающей запятой.
В старых машинах, использовавших фиксированное размещение запятой, положение последней в разрядной сетке ЭВМ было заранее обусловлено – раз и навсегда для всех чисел и для всех технических устройств. Поэтому отпадала необходимость в каком-либо способе ее указания во внутреннем представлении чисел. Все вычислительные алгоритмы были заранее "настроены" на это фиксированное размещение.
Слайд 10Представление с плавающей запятой
любое число A в системе счисления с основанием Q
Представление с плавающей запятой
любое число A в системе счисления с основанием Q

A = (± M) x Q ± P.
где M называют мантиссой, а показатель степени P - порядком числа.
Например, 0,03 = 3 х 10 -2 = 30 х 10 -3 = 0,3 х 10 -1 = 0,03 х 10 0 = ... То есть, представление числа с плавающей запятой не является единственным. Поэтому договорились для выделения единственного варианта записи числа считать, что мантисса всегда меньше единицы, а ее первый разряд содержит отличную от нуля цифру – в нашем примере обоим требованиям удовлетворит только число 0,3 х 10 -1.
Описанное представление чисел называется нормализованным и является единственным. Любое число может быть нормализовано. Особо подчеркнем, что требования к нормализации чисел вводятся исходя из соображений обеспечения максимальной точности их представления.
Слайд 11Представление с плавающей запятой
Все сказанное о нормализации можно применять и к двоичной
Представление с плавающей запятой
Все сказанное о нормализации можно применять и к двоичной

A = (± M) x 2 ± P.
Например: - 3 10 = - 0,11 x 210, M = 0,11 и P = 10.
Существенно, что двоичная мантисса всегда начинается с единицы. Поэтому во многих ЭВМ эта единица не записывается в ОЗУ, что позволяет сохранить еще один дополнительный разряд мантиссы (так называемая скрытая единица).
Арифметика чисел с плавающей запятой оказывается заметно сложнее, чем с фиксированной. Например, чтобы сложить два числа с плавающей запятой, требуется предварительно привести их к представлению, когда оба порядка равны; такую процедуру принято называть выравниванием порядков. Кроме того, в результате вычислений нормализация часто нарушается, а значит необходимо ее восстанавливать. Тем не менее, вычислительные машины со всем этим великолепно умеют автоматически справляться, и именно такой способ вычислений лежит в основе работы современных компьютеров.
Слайд 12Представление с плавающей запятой
при использовании метода представления вещественных чисел с плавающей запятой
Представление с плавающей запятой
при использовании метода представления вещественных чисел с плавающей запятой

Для того чтобы сохранить максимальную точность, вычислительные машины почти всегда хранят мантиссу в нормализованном виде, что означает, что мантисса в данном случае есть число, лежащее между 1(10) и 2(10) (1 < M < 2). Способ хранения мантиссы с плавающей точкой подразумевает, что двоичная запятая находится на фиксированном месте. Фактически подразумевается, что двоичная запятая следует после первой двоичной цифры, т.е. нормализация мантиссы делает единичным первый бит, помещая тем самым значение между единицей и двойкой. Место, отводимое для числа с плавающей точкой, делится на два поля. Одно поле содержит знак и значение мантиссы, а другое содержит знак и значение порядка.
Слайд 13Вещественные типы данных
Для типа double:
Вещественные типы данных
Для типа double:
Слайд 14Представление чисел с плавающей запятой
Для упрощения вычислений и сравнения действительных чисел значение
Представление чисел с плавающей запятой
Для упрощения вычислений и сравнения действительных чисел значение

Алгоритм для получения представления действительного числа в памяти ЭВМ:
Перевести модуль данного числа в двоичную систему счисления;
нормализовать двоичное число, т.е. записать в виде M × 2p, где M — мантисса (ее целая часть равна 1(2)) и p — порядок, записанный в десятичной системе счисления;
прибавить к порядку смещение и перевести смещенный порядок в двоичную систему счисления;
учитывая знак заданного числа (0 — положительное; 1 — отрицательное), выписать его представление в памяти ЭВМ.
Слайд 15Пример:
Запишем код числа -312,3125.
Двоичная запись модуля этого числа имеет вид 100111000,0101.
Проведем
Пример:
Запишем код числа -312,3125.
Двоичная запись модуля этого числа имеет вид 100111000,0101.
Проведем

Находим смещенный порядок: 8 + 1023 = 1031. Далее имеем 1031(10) = 10000000111(2).
Окончательно
Очевидно, что более компактно полученный код стоит записать следующим образом: C073850000000000(16).
Слайд 16Обратный переход от кода действительного числа к самому числу
Пусть дан код 3FEC600000000000(16)
Обратный переход от кода действительного числа к самому числу
Пусть дан код 3FEC600000000000(16)

Прежде всего замечаем, что это код положительного числа, поскольку в разряде с номером 63 записан нуль. Получим порядок этого числа: 01111111110(2) = 1022(10); 1022 - 1023 = -1.
Число имеет вид 1,1100011 × 2-1 или 0,11100011.
Переводом в десятичную систему счисления получаем 0,88671875.
Слайд 17Представление текстовой информации
Текстовая информация, как и любая другая, хранится в памяти компьютера
Представление текстовой информации
Текстовая информация, как и любая другая, хранится в памяти компьютера

В персональных компьютерах обычно используется система кодировки ASCII (American Standard Code for Information Interchange - американский стандартный код для обмена информации). Он введен в 1963 г. и ставит в соответствие каждому символу семиразрядный двоичный код. Легко определить, что в коде ASCII можно представить 128 символов.
В системе ASCII закреплены две таблицы кодирования базовая и расширенная. Базовая таблица закрепляет значения кодов от 0 до 127, а расширенная относится к символам с номерами от 128 до 255. Первые 32 кода базовой таблицы, начиная с нулевого, отданы производителям аппаратных средств. В этой области размещаются управляющие коды, которым не соответствуют ни какие символы языков. Начиная с 32 по 127 код размещены коды символов английского алфавита, знаков препинания, арифметических действий и вспомогательных символов.
Слайд 18Таблица ASCII
Таблица ASCII

 Зодчество Галицкой земли 12 века
Зодчество Галицкой земли 12 века Внешняя политика России
Внешняя политика России Прощание с Букварем
Прощание с Букварем Презентация на тему Реформация и Контрреформация в Европе
Презентация на тему Реформация и Контрреформация в Европе  Ася. Иван Тургенев
Ася. Иван Тургенев Диаграммы и графики.
Диаграммы и графики. © Министерство информатизации и связи Красноярского края 2012 г. Вебинар для сотрудников ОМСУ Красноярского края: - Готовность Реест
© Министерство информатизации и связи Красноярского края 2012 г. Вебинар для сотрудников ОМСУ Красноярского края: - Готовность Реест Языческие праздники на Руси
Языческие праздники на Руси Fandrayzing
Fandrayzing Г. А. Цукерман, К. Н. Поливанова
Г. А. Цукерман, К. Н. Поливанова Генетический анализ вместо химиотерапии
Генетический анализ вместо химиотерапии Презентация на тему Театр в XVIII веке в России
Презентация на тему Театр в XVIII веке в России  Инженерная компьютерная графика
Инженерная компьютерная графика Акробатические элементы
Акробатические элементы Презентация_МР_Чистодей
Презентация_МР_Чистодей РЕАБИЛИТАЦИЯ СЕГОДНЯ и ЗАВТРА Докладчик: Булекбаева Ш.А., Председатель Правления АО РДРЦ, дмн, внештатный медицинский реабилитолог
РЕАБИЛИТАЦИЯ СЕГОДНЯ и ЗАВТРА Докладчик: Булекбаева Ш.А., Председатель Правления АО РДРЦ, дмн, внештатный медицинский реабилитолог Обратная пропорциональность
Обратная пропорциональность Уважаеми работодатели,
Уважаеми работодатели, Генограмма семьи
Генограмма семьи Polish language
Polish language Gobozov
Gobozov Презентация "Азбука Архитектуры" - скачать презентации по МХК
Презентация "Азбука Архитектуры" - скачать презентации по МХК Основные положения закона Российской Федерации в области физической культуры, спорта, туризма, охраны здоровья
Основные положения закона Российской Федерации в области физической культуры, спорта, туризма, охраны здоровья Роза
Роза Деловая графика MS Exel
Деловая графика MS Exel Білезік фото
Білезік фото 4
4 Методическая разработка мастер-класса
Методическая разработка мастер-класса