Эйлер стал студентом факультета искусств Базельского университета.
4 июня 1724 года, Эйлер произнёс по латыни великолепную речь о сравнении философских воззрений Декарта и Ньютона — и был удостоен учёной степени магистра.
5 апреля 1727 года, Эйлер навсегда покидает Швейцарию, по совету братьев Бернулли его пригласили стать адъюнктом по физиологии в Санкт-Петербурге.
1733 год. 26-летний Леонард Эйлер женился на дочери живописца Екатерине Гзель, которой в это время тоже было 26 лет.
1736 год. Издано двухтомное сочинение «Механика, или наука о движении, в аналитическом изложении».
1741 год. В соответствии с поданным Эйлером прошением, он был «отпущен от Академии» и утверждён почётным академиком. Он обещал по мере своих сил помогать Петербургской Академии — и действительно помогал весьма существенно все 25 лет, пока не вернулся обратно в Россию. В июне 1741 г. Леонард Эйлер с женой, двумя сыновьями и четырьмя племянниками прибыл в Берлин.
1757 год. Эйлер впервые в истории нашёл формулы для определения критической нагрузки при сжатии упругого стержня. Однако в те годы эти формулы не могли найти практического применения.
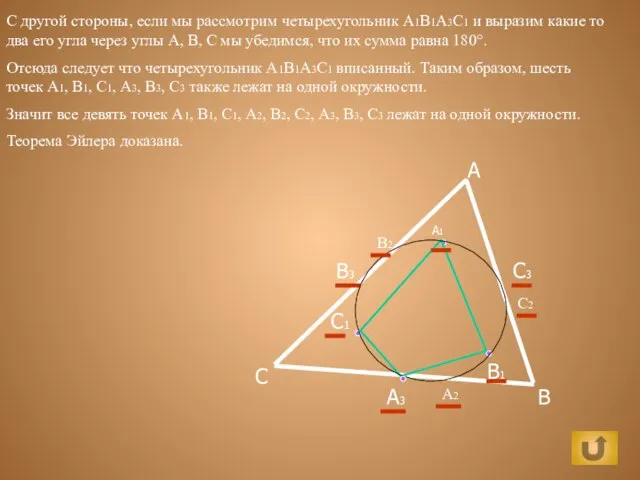
Леонардо Эйлер





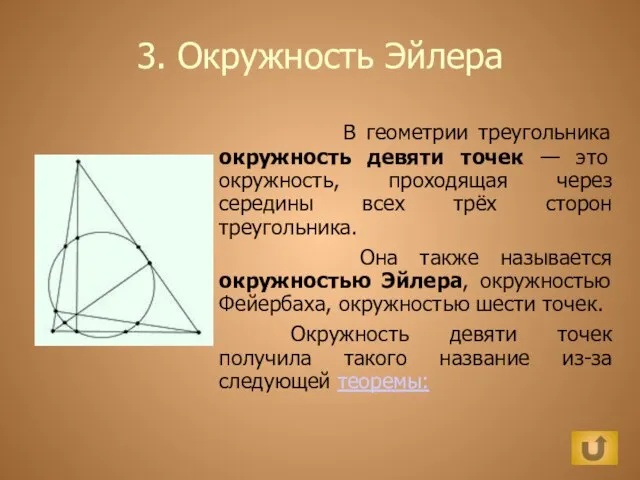


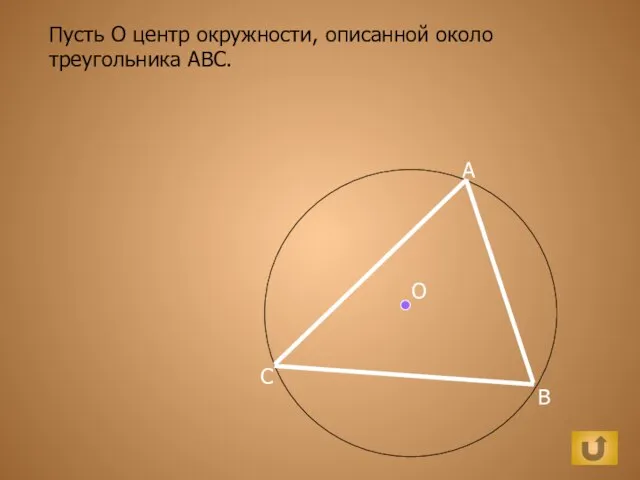
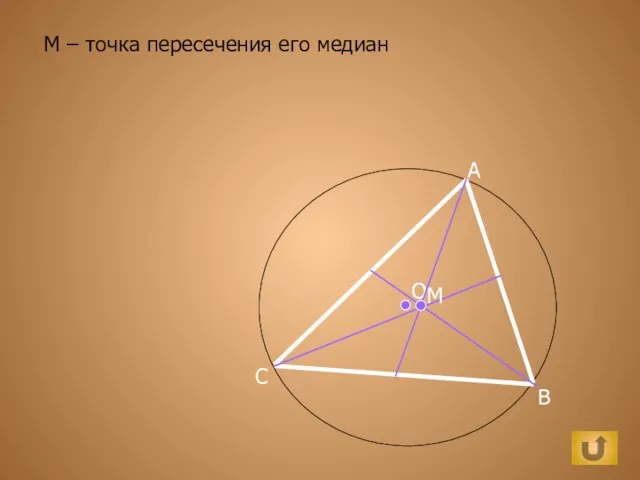
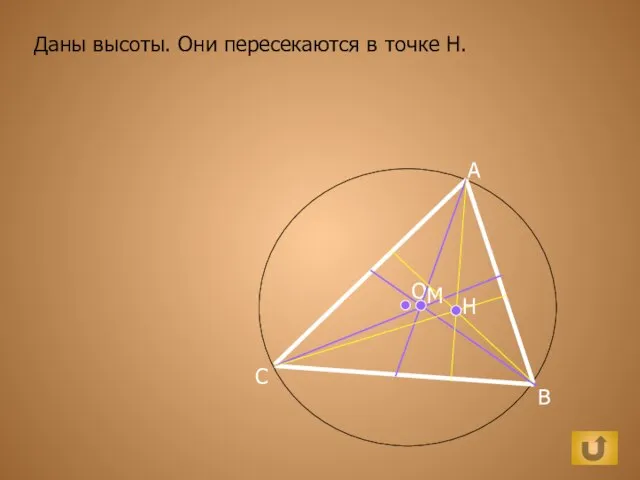
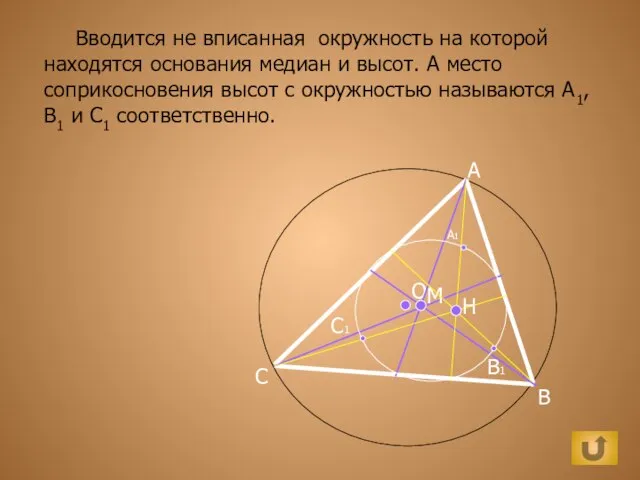
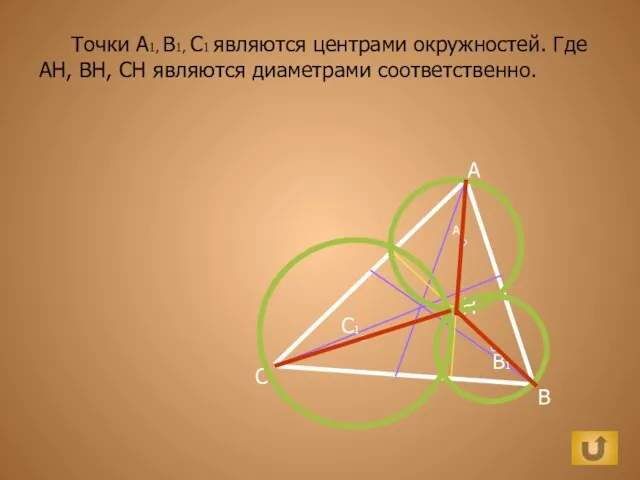
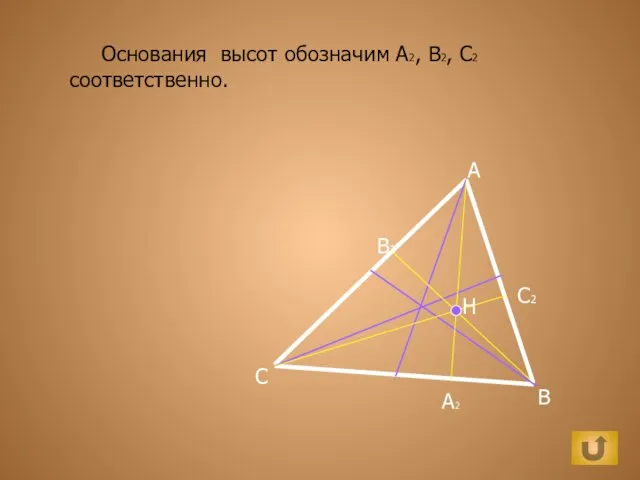
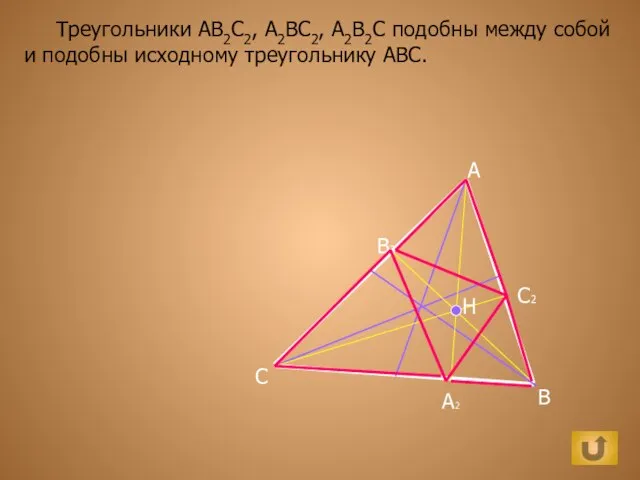



 Готика
Готика Культура итальянского возрождения
Культура итальянского возрождения Поэтический перевод как средство развития одарённых детей
Поэтический перевод как средство развития одарённых детей Кто я, мои интересы, как я вижу себя в профессии
Кто я, мои интересы, как я вижу себя в профессии Экспериментальный сад Лоулайн Лэб (Lowline Lab)
Экспериментальный сад Лоулайн Лэб (Lowline Lab) Служба в резерве вооруженных сил России Б.А.Р.С
Служба в резерве вооруженных сил России Б.А.Р.С Святки-колядки
Святки-колядки Методы стимулирования продажи товаров. Шаблон
Методы стимулирования продажи товаров. Шаблон Object, the objects and components of computer science
Object, the objects and components of computer science Смешанные леса
Смешанные леса Аудит дорожной безопасности – инструмент снижения риска человеческой ошибки на дороге Шабашева Мария Ведущий инженер ОО
Аудит дорожной безопасности – инструмент снижения риска человеческой ошибки на дороге Шабашева Мария Ведущий инженер ОО АППЛИКАЦИЯ ИЗ НИТОК
АППЛИКАЦИЯ ИЗ НИТОК Вскрытие и опробование продуктивных горизонтов. Разведочный этап исследований
Вскрытие и опробование продуктивных горизонтов. Разведочный этап исследований Керамзитовый песок
Керамзитовый песок Ради жизни на земле
Ради жизни на земле Стандартизация криптографических методов защиты информации в России и за рубежом
Стандартизация криптографических методов защиты информации в России и за рубежом Построение изображений в линзах
Построение изображений в линзах История и методология науки публичного управления
История и методология науки публичного управления Гражданские правоотношения. Тема №2
Гражданские правоотношения. Тема №2 Школьники и здоровое питание
Школьники и здоровое питание 2_фонетика
2_фонетика Автоматизация звуков р и рь
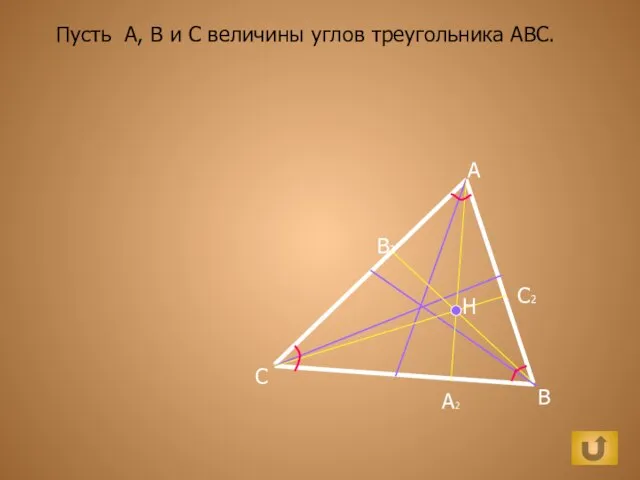
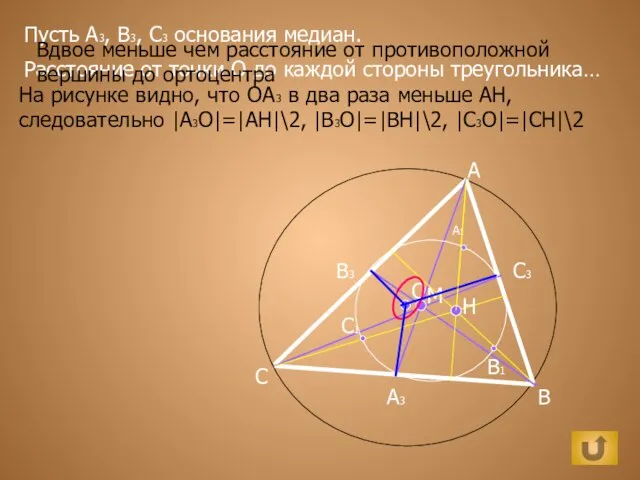
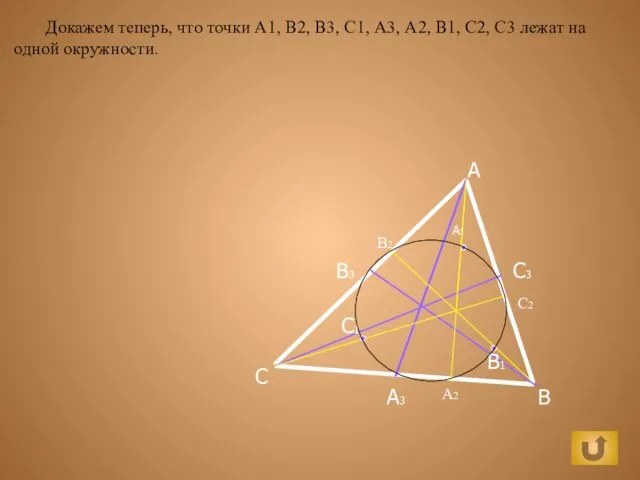
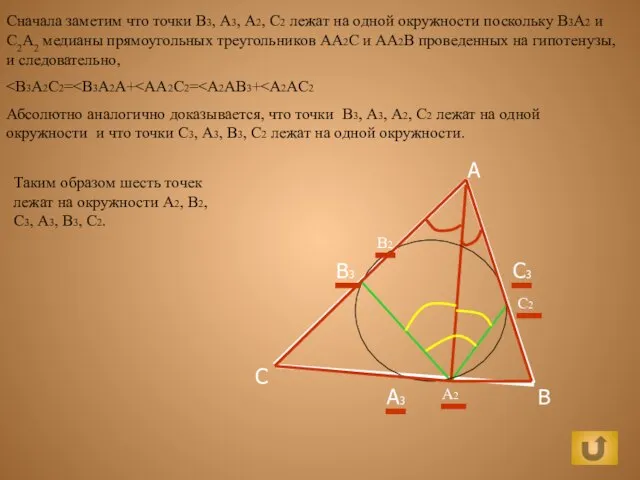
Автоматизация звуков р и рь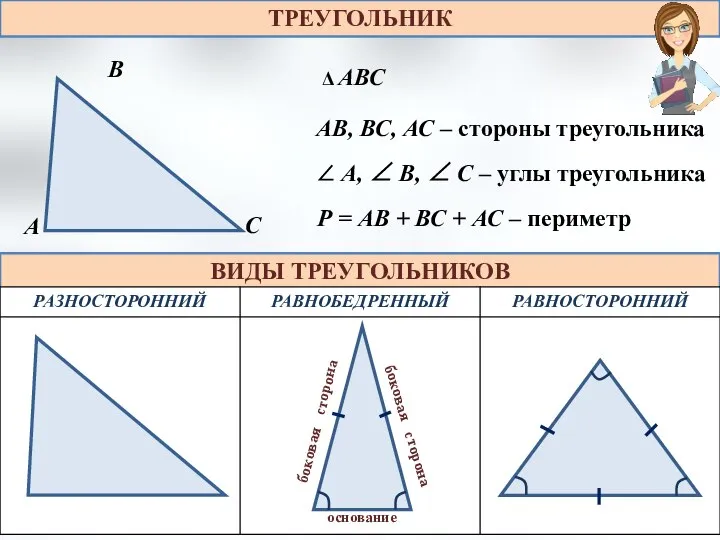 Сумма углов треугольника
Сумма углов треугольника ЗЕНКОВ МАКСИМ ЮРЬЕВИЧ
ЗЕНКОВ МАКСИМ ЮРЬЕВИЧ Техника мраморирования в современном дизайне
Техника мраморирования в современном дизайне Presentation Title
Presentation Title  Рязанский Кремль Всё о Нём
Рязанский Кремль Всё о Нём Подготовила воспитатель ГБОУ ЦО№491 «Марьино» д/п 1468 Виноградова Галина Константиновна
Подготовила воспитатель ГБОУ ЦО№491 «Марьино» д/п 1468 Виноградова Галина Константиновна