Содержание
- 2. Содержание: Построение функции Лагранжа Необходимое условие минимума Пример Необходимые условия Нерегулярный и регулярный случаи Продолжение Завершение
- 3. Построение функции Лагранжа Метод множителей Лагранжа - это метод решения задач на условный экстремум; метод множителей
- 4. Необходимое условие минимума Если x*-точка локального минимума в поставленной задаче, то существуют множители Лагранжа , не
- 5. Пример Решить экстремальную задачу Решение Составим функцию Лагранжа: назад
- 6. Необходимые условия Запишем необходимые условия минимума а). Стационарности б). Дополняющей нежесткости в). Неотрицательности или согласования знаков
- 7. Нерегулярный и регулярный случаи 1. Нерегулярный случай: - все множители Лагранжа – нули, что противоречит условию
- 9. Скачать презентацию






 April Fool’s Day
April Fool’s Day Россия в эпоху петровских преобразований
Россия в эпоху петровских преобразований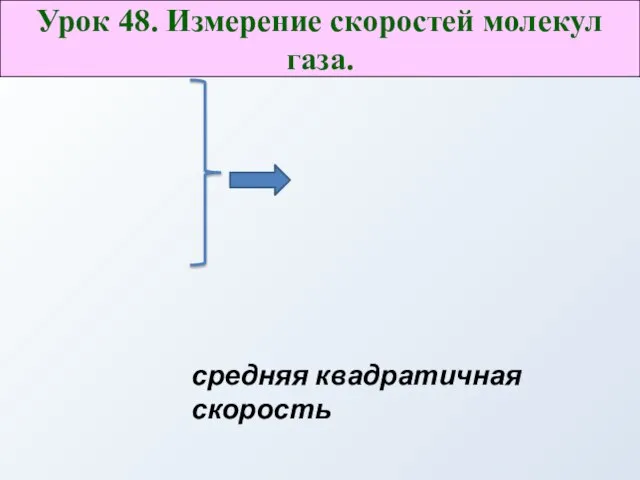 Измерение скоростей молекул газа
Измерение скоростей молекул газа Проектирование транспортных машин (ТМ)
Проектирование транспортных машин (ТМ) Архитектура распределённых приложений
Архитектура распределённых приложений ЭКВАТОРИАЛЬНЫЕ ЛЕСА
ЭКВАТОРИАЛЬНЫЕ ЛЕСА Все начиналось в XVIII веке
Все начиналось в XVIII веке ОНКОЛОГИЧЕСКИЙ ЦЕНТР НОВЫЕ МЕТОДЫ ДИАГНОСТИКИ Клиника ОАО «Медицина» Всё лучшее в медицине! - презентация
ОНКОЛОГИЧЕСКИЙ ЦЕНТР НОВЫЕ МЕТОДЫ ДИАГНОСТИКИ Клиника ОАО «Медицина» Всё лучшее в медицине! - презентация Государственное регулирование транспортной системы в городе федерального значения Москве
Государственное регулирование транспортной системы в городе федерального значения Москве Свойства почвы, воздуха и воды.
Свойства почвы, воздуха и воды. Научно – практическая конференция по экологии
Научно – практическая конференция по экологии Итоги социально-экономического развития Смоленской области за 1 квартал 2011 года
Итоги социально-экономического развития Смоленской области за 1 квартал 2011 года Презентация на тему Моя профессия - строитель
Презентация на тему Моя профессия - строитель География мировых природных ресурсов
География мировых природных ресурсов АРБИТРАЖНОЕ СОГЛАШЕНИЕ И АРБИТРАЖНАЯ ОГОВОРКА ВО ВНЕШНЕТОРГОВЫХ КОНТРАКТАХ. Выполнили Улан кызы Айгерим, Раджабиен Сарвари
АРБИТРАЖНОЕ СОГЛАШЕНИЕ И АРБИТРАЖНАЯ ОГОВОРКА ВО ВНЕШНЕТОРГОВЫХ КОНТРАКТАХ. Выполнили Улан кызы Айгерим, Раджабиен Сарвари Презентация на тему Первые общерусские князья (10 класс)
Презентация на тему Первые общерусские князья (10 класс) Припадаю, Россия, к твоей красоте
Припадаю, Россия, к твоей красоте Что изменилось в правилах госзакупок в 2016 году
Что изменилось в правилах госзакупок в 2016 году Этимологический словарь Макса Фасмера
Этимологический словарь Макса Фасмера Презентация на тему Суффиксы -ек и -ик в именах существительных
Презентация на тему Суффиксы -ек и -ик в именах существительных В. Солоухин "За правым и левым плечом"
В. Солоухин "За правым и левым плечом" Процессы памяти и их нарушения при нервно-психических заболеваниях
Процессы памяти и их нарушения при нервно-психических заболеваниях Комбинат “Крымская Роза”
Комбинат “Крымская Роза” Автономное выживание человека в природе
Автономное выживание человека в природе 8 класс I тур 2006-2007 г.
8 класс I тур 2006-2007 г. Презентация Семенов (3) (1)
Презентация Семенов (3) (1) Презентация на тему Распад СССР
Презентация на тему Распад СССР  В музыкальном театре
В музыкальном театре