Содержание
- 2. Подходы для математического описания ламинарных реагирующих потоков (пламен) Аналитические методы: тепловая и цепная теории распространения пламени
- 3. Термодинамико-кинетические программные комплексы «Химический верстак» (Chemical workbench) www.kintech.ru/ Институт высоких температур, Россия KINTECUS www.kintecus.com COSILAB www.rotexo.com/cms
- 4. CHEMKIN CHEMKIN представляет собой пакет программного обеспечения, содержащий множество процедур и функций, облегчающих постановку задач, связанных
- 5. Программа PREMIX (из пакета CHEMKIN) стабилизированное на горелке пламя, в которой температуры определены из уравнения сохранения
- 6. Уравнения сохранения в пламени: Уравнение непрерывности: Ṁ - массовый расход, ρ - массовая плотность, u -
- 7. Уравнения сохранения в пламени: Уравнение сохранения энергии: x- пространственная координата, Ṁ - массовый расход, Yk -
- 8. Уравнения сохранения в пламени: Уравнение сохранения компонентов: x- пространственная координата, Ṁ - массовый расход, Yk -
- 9. Уравнения сохранения в пламени: Уравнение состояния W - средний молекулярный вес смеси, - массовая плотность, T
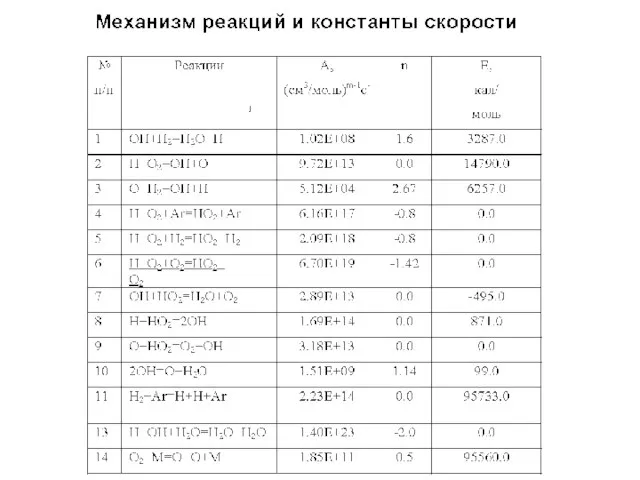
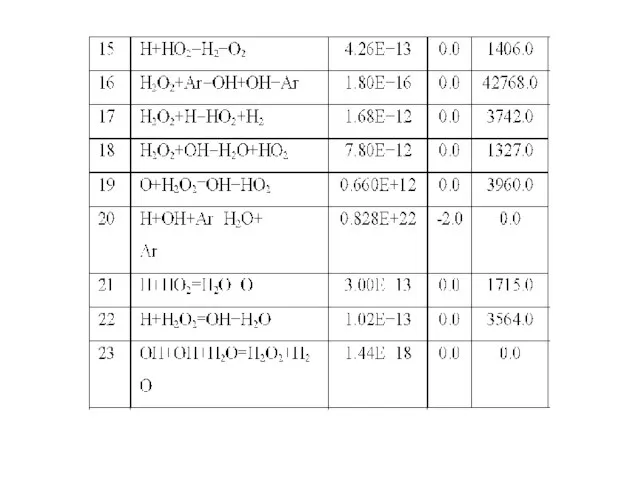
- 10. Кинетика элементарных реакций Модифицированный вид Аррениусовской зависимости константы скорости от Т:
- 11. Термодинамические базы данных Термодинамические данные, используемые программой CHEMKIN, представлены в виде термохимических таблиц JANAF. Термодинамические данные
- 12. Транспортные свойства межмолекулярные взаимодействия описаны потенциалом Леннарда-Джонса Потенциал характеризуется диаметром молекулы и глубиной межмолекулярного потенциала
- 13. Формула для диффузионной скорости смеси где - мольная доля компонента, и где Dk коэффициент диффузии усредненной
- 14. Метод решения Численная процедура решения: конечно-разносные методы - приведение задачи к системе алгебраических уравнений. Начальное приближение
- 15. Граничные условия. Для стабилизированного на горелке пламени сохраняется скорость массового потока Температура и массовая скорость компонентов
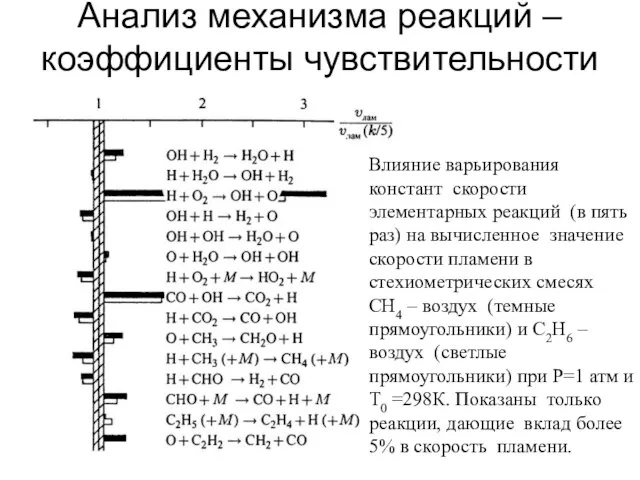
- 18. Анализ механизма реакций – коэффициенты чувствительности Влияние варьирования констант скорости элементарных реакций (в пять раз) на
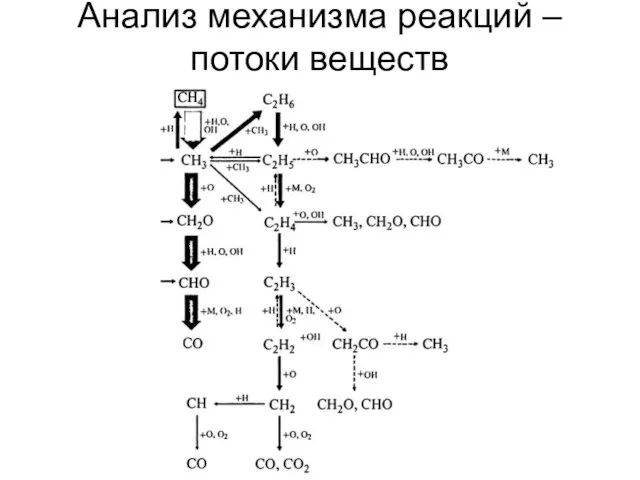
- 19. Анализ механизма реакций – потоки веществ
- 20. СТРУКТУРА ЛАМИНАРНОГО ПЛАМЕНИ ПЕРЕМЕШАННОЙ СМЕСИ H2/O2/Ar
- 23. Профили мольных долей стабильных компонентов в пламени: точки– эксперимент; сплошная линия – расчет P=40 торр Расстояние
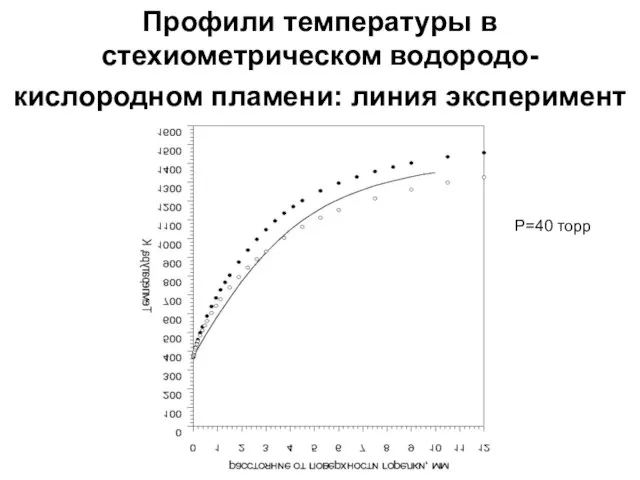
- 24. Профили температуры в стехиометрическом водородо-кислородном пламени: линия эксперимент P=40 торр
- 26. Скачать презентацию
















 Презентация на тему: Куликовская битва и ее историческое значение Работу выполнил : студент 1-го курса ЮБ 02/1402 Куликов Андрей
Презентация на тему: Куликовская битва и ее историческое значение Работу выполнил : студент 1-го курса ЮБ 02/1402 Куликов Андрей Пчелиный мед
Пчелиный мед Итоги января 2011 года
Итоги января 2011 года Методы изучения реакций с участием свободных радикалов:1. Электронный парамагнитный резонанс 2. Хемилюминесценция3. Биохимическ
Методы изучения реакций с участием свободных радикалов:1. Электронный парамагнитный резонанс 2. Хемилюминесценция3. Биохимическ Альберт Эйнштейн
Альберт Эйнштейн Особенности интеграции системы образования Донецкой Народной Республики в российское образовательное пространство
Особенности интеграции системы образования Донецкой Народной Республики в российское образовательное пространство My Trip to the UK
My Trip to the UK Маркшейдерские работы на открытых разработках месторождений золота
Маркшейдерские работы на открытых разработках месторождений золота Презентация на тему Культура Западной Европы в XI – XV вв
Презентация на тему Культура Западной Европы в XI – XV вв Свеча
Свеча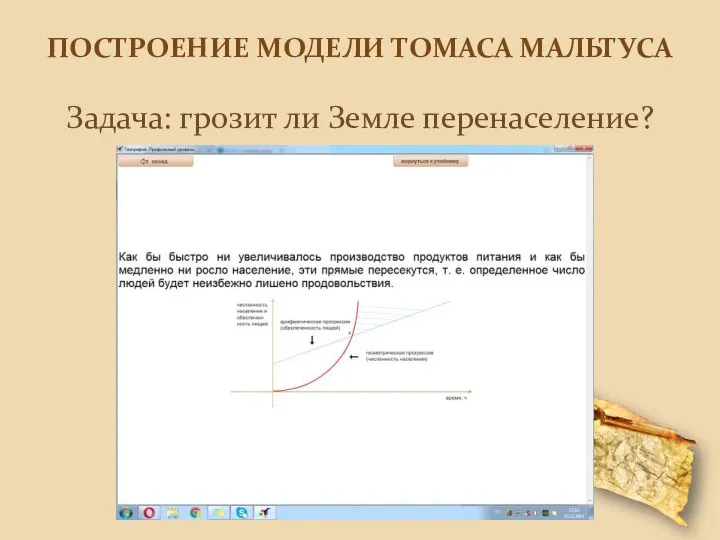 Построение модели Томаса Мальтуса. Грозит ли Земле перенаселение
Построение модели Томаса Мальтуса. Грозит ли Земле перенаселение СЕМИНАР по вопросу разработки, представления и регистрации в органах государственного пожарного надзора МЧС России деклараций
СЕМИНАР по вопросу разработки, представления и регистрации в органах государственного пожарного надзора МЧС России деклараций  Волейбол
Волейбол Понятие маркетинговых исследований
Понятие маркетинговых исследований Вкусные числа
Вкусные числа Керамика
Керамика Презентация на тему Флаги России От первого до современного
Презентация на тему Флаги России От первого до современного Как любить ребенка
Как любить ребенка Цифровая модель системы внешнего электроснабжения линии метрополитена с использованием программного комплекса ETAP
Цифровая модель системы внешнего электроснабжения линии метрополитена с использованием программного комплекса ETAP Герои: II сезон
Герои: II сезон Презентация на тему Отдел моховидные
Презентация на тему Отдел моховидные The Flag of The United Kingdom
The Flag of The United Kingdom Проект «Work & Move»
Проект «Work & Move» Лёгкая и пищевая промышленность – 7 класс
Лёгкая и пищевая промышленность – 7 класс И. С. Тургенев «Бирюк»
И. С. Тургенев «Бирюк» Разные типы занятий и их роль в экологическом воспитании детей
Разные типы занятий и их роль в экологическом воспитании детей Сложение и вычитание двузначных чисел 2 класс
Сложение и вычитание двузначных чисел 2 класс Организация исследовательской деятельности инструментами ТРИЗ-педагогики
Организация исследовательской деятельности инструментами ТРИЗ-педагогики