Презентация к уроку геометрии по теме: «ДВИЖЕНИЕ.ВИДЫ ДВИЖЕНИЯ» 9 класс Учитель: Юрко Оксана Александровна, учитель математики МОУ

БОЖЕСТВЕННАЯ СИММЕТРИЯ

СОДЕРЖАНИЕ
ВВЕДЕНИЕ.
1.ДВИЖЕНИЕ. ВИДЫ ДВИЖЕНИЯ.
2.КТО ПРИДУМАЛ СИММЕТРИЮ?
3.СИММЕТРИЧЕН ЛИ ЧЕЛОВЕК?
4.СИММЕТРИЯ В АРХИТЕКТУРЕ.
5.ФРАНЦУЗСКИЕ САДЫ.
6.СИММЕТРИЯ В СТРОЕНИИ ЖИВОТНЫХ.
ЗАКЛЮЧЕНИЕ.
СПИСОК ЛИТЕРАТУРЫ.

Данная работа посвящена такому математическому понятию как «движение» и её видам, в частности, симметрии.
СИММЕТРИЯ.
Симметрия пронизывает буквально все вокруг, захватывая, казалось бы, совершенно неожиданные области и объекты.

Симметрия устанавливает забавное и удивительное сродство между предметами, явлениями и теориями, внешне, казалось бы, ничем не связанными.
Дж. Ньюмен

1. ДВИЖЕНИЕ. ВИДЫ ДВИЖЕНИЯ.
ДВИЖЕНИЕ – преобразование фигуры F в фигуру F1 , которое сохраняет расстояние между точками, т. е. переводит любые две точки А и В фигуры F в точки А1 и В1 фигуры F1 так, что АВ=А1В1.

СВОЙСТВА ДВИЖЕНИЯ:
1.Точки, лежащие на прямой, переходят в точки, лежащие на прямой.
2. Прямые переходят в прямые, полупрямые – в полупрямые, отрезки – в отрезки.
3. Сохраняются углы между полупрямыми.
4. Плоскость переходит в плоскость.
О. Два движения, выполненные последовательно, дают снова движение. Результат выполнения этих движений называется композицией движения.

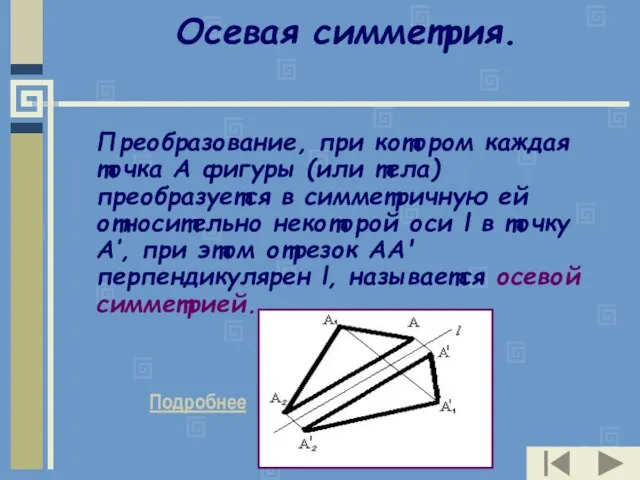
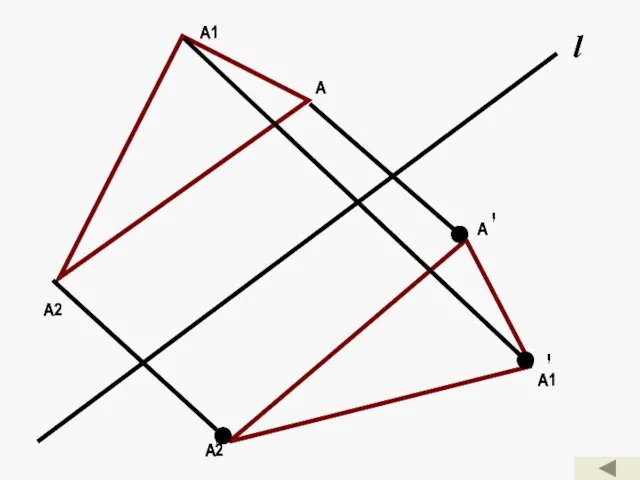
Осевая симметрия.
Преобразование, при котором каждая точка А фигуры (или тела) преобразуется в симметричную ей относительно некоторой оси l в точку А’, при этом отрезок АА' перпендикулярен l, называется осевой симметрией.
Подробнее

А1
А
А2
А2
А1
А
l
А1
А
А2
А2
А1
А
l

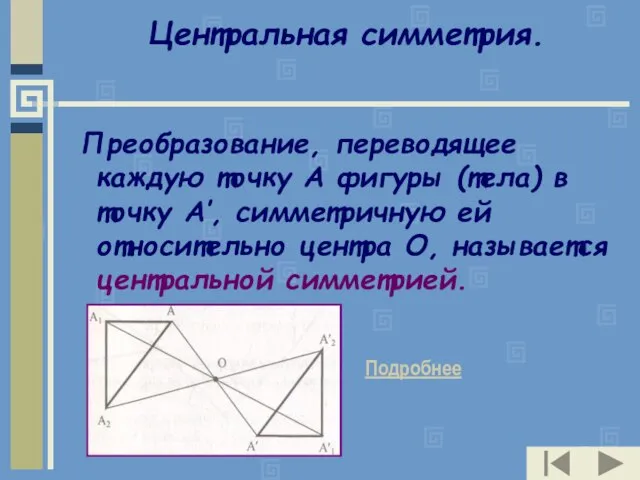
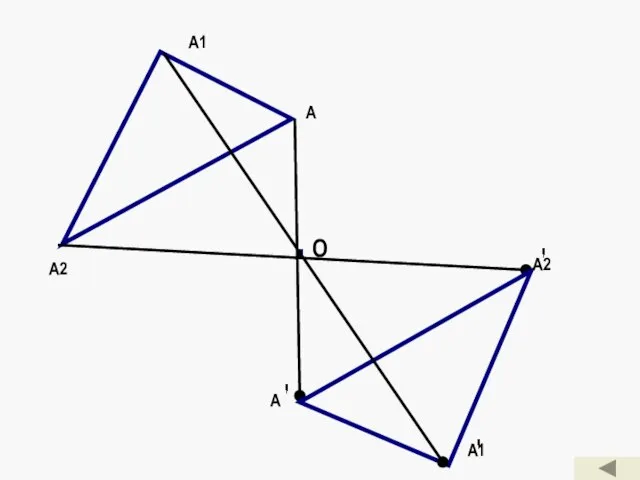
Центральная симметрия.
Преобразование, переводящее каждую точку А фигуры (тела) в точку А′, симметричную ей относительно центра О, называется центральной симметрией.
Подробнее

А1
А
А2
. О
А2
А1
А

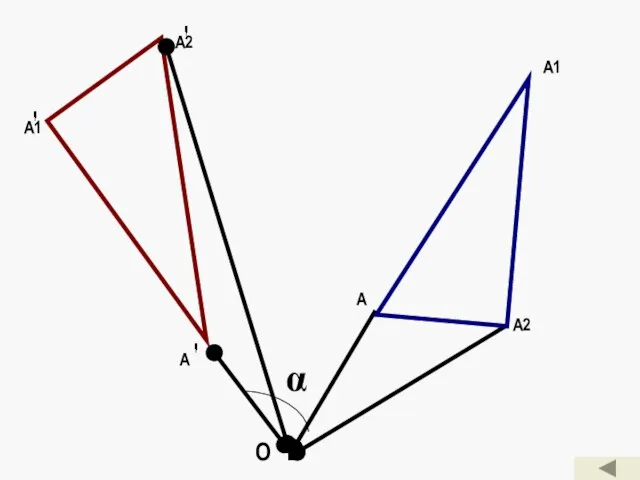
Поворот.
Преобразование, при котором каждая точка А фигуры (тела) поворачивается на один и тот же угол α вокруг заданного центра О, называется вращением или поворотом плоскости.
Подробнее

А
А2
А2
А1
А
А1
α
О .

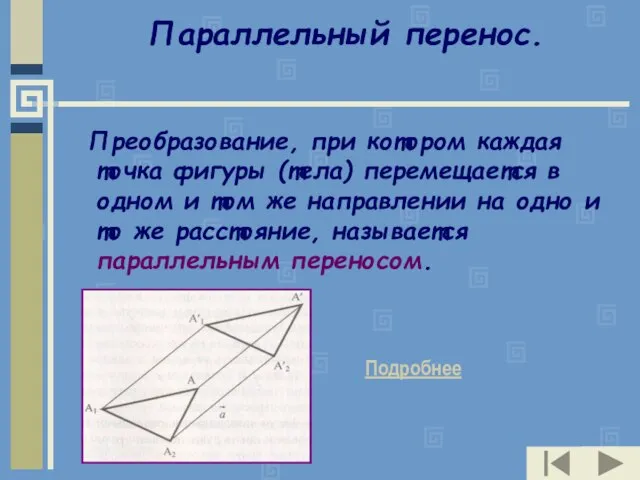
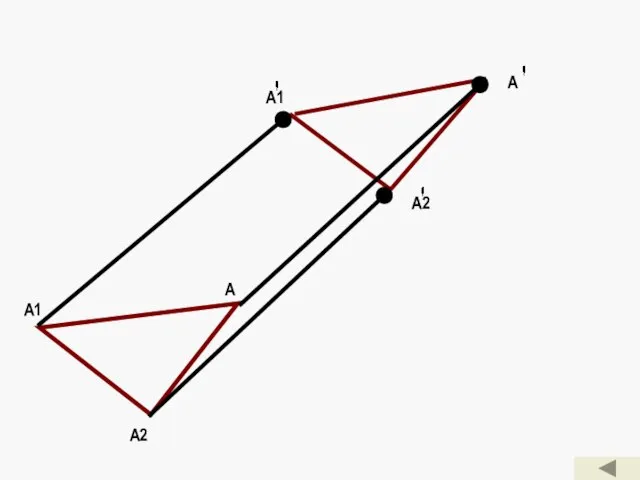
Параллельный перенос.
Преобразование, при котором каждая точка фигуры (тела) перемещается в одном и том же направлении на одно и то же расстояние, называется параллельным переносом.
Подробнее

А2
А
А2
А1
А
А1

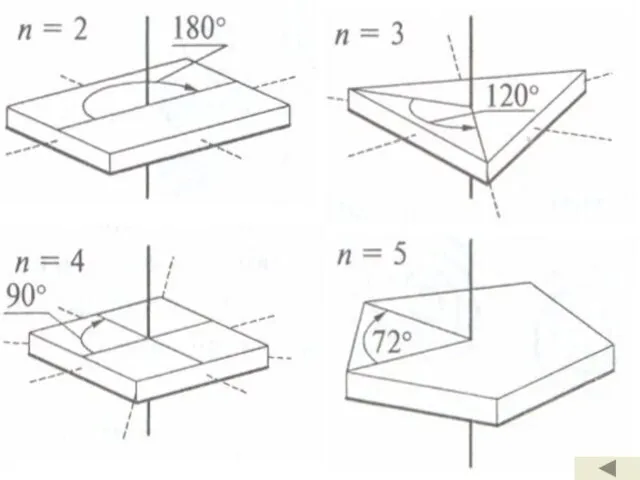
Поворотная симметрия.
Предположим, что объект совмещается сам с собой при повороте вокруг некоторой оси на угол, равный 360˚/n, где n=2,3,4,… В этом случае говорят о поворотной симметрии, а указанную ось называют поворотной осью n-го порядка. (рисунок)

2. КТО ПРИДУМАЛ СИММЕТРИЮ ?
По преданию, древнегреческий скульптор, Пифагор Регийский придумал термин «симметрия».
ИСТОРИЧЕСКАЯ СПРАВКА.
Пифагор Регийский (V век до н. э.) — древнегреческий скульптор периода ранней классики, его работы известны лишь по упоминаниям древних авторов.
Пифагору Регийскому приписывают, найденную в Дельфах, знаменитую бронзовую статую «Возничий».

Пифагор Регийский. «Мальчик, вынимающий занозу»
(римская копия).
Легенда гласит, что эта статуя была отлита в честь юного спартанца, победившего в беге, несмотря на то, что его ногу пронзил острый шип.

«Раненая амазонка»
Сегодня существует ещё и версия о том, что греческий скульптор Поликлет ( V век до н. э.) тоже использовал термин «симметрия».
«Раненая амазонка», 440—430 до н. э.

СИММЕТРИЧЕН ЛИ ЧЕЛОВЕК ?
Почему одни люди кажутся нам более привлекательными, чем другие?
Оказывается всё дело в симметрии человеческого тела.
Сходство между нашими руками, глазами и другими частями тела такое же, как между предметом и его отражением в зеркале.
Это пример зеркальной симметрии.

СИММЕТРИЧЕН ЛИ ЧЕЛОВЕК ?

СИММЕТРИЯ В АРХИТЕКТУРЕ.
Очень часто с симметрией мы встречаемся в архитектуре.
Так многие фасады зданий обладают симметрией

СИММЕТРИЯ И МОСТЫ.

ФРАНЦУЗСКИЕ САДЫ.
Именно во Франции изысканно сложный и симметрично спланированный сад приобрел статус совершенного творения и стал эталоном садового дизайна.
И приобрел название «французский».

ИСТОРИЧЕСКАЯ СПРАВКА.
Родоначальником стиля стал Андре Ленотр – королевский садовник.
Он следуя королевскому приказу, начал создавать парк Версаль – как символ безграничного могущества «короля-солнца» Людовика XIV.

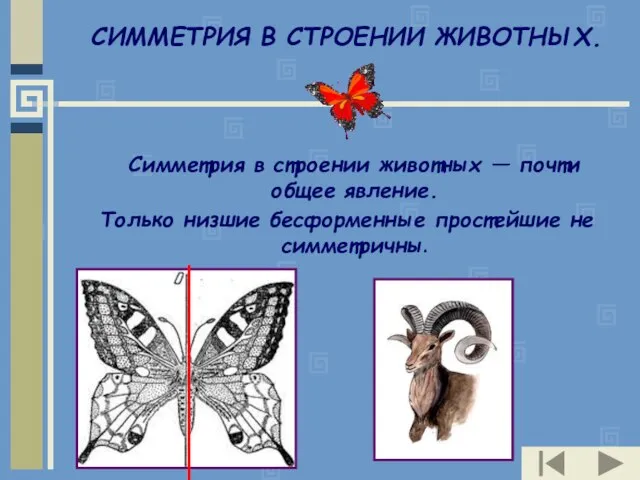
СИММЕТРИЯ В СТРОЕНИИ ЖИВОТНЫХ.
Симметрия в строении животных — почти общее явление.
Только низшие бесформенные простейшие не симметричны.

ЗАКЛЮЧЕНИЕ.
Симметрия – играет большую роль, как в природе, так и в жизни человека.
Большинство растений и животных симметричны, также симметрия есть и в архитектурных сооружениях, и даже в самых простых вещах, которые нас окружают.