Презентация Лек 11 валы и оси

Назначение, классификация ВиО, применение в МГКМ.
Определения:
Вал – деталь машины или механизма предназначенная для передачи вращающего или крутящего момента вдоль своей осевой линии (рис. 9.1).
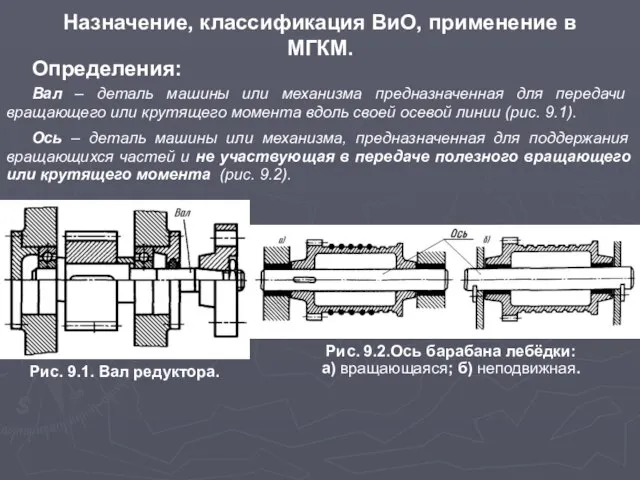
Ось – деталь машины или механизма, предназначенная для поддержания вращающихся частей и не участвующая в передаче полезного вращающего или крутящего момента (рис. 9.2).
Рис. 9.1. Вал редуктора.
Рис. 9.2.Ось барабана лебёдки:
а) вращающаяся; б) неподвижная.

Классификация валов и осей:
1. По форме продольной геометрической оси −
1.1. прямые (продольная ось – прямая линия), валы редукторов, валы коробок передач гусеничных и колёсных машин;
1.2. коленчатые (продольная геометрическая ось разделена на несколько параллельных отрезков, смещённых друг относительно друга в радиальном направлении), например, коленвал двигателя внутреннего сгорания;
1.3. гибкие (продольная геометрическая ось является линией переменной кривизны, изменяемой в процессе работы механизма или при монтажно-демонтажных мероприятиях), вал привода спидометра автомобилей.
2. По функциональному назначению −
2.1. валы передач, они несут на себе элементы, передающие вращающий момент (зубчатые или червячные колёса, шкивы, звёздочки, муфты и т.п.) и в большинстве своём снабжены концевыми частями, выступающими за габариты корпуса механизма;
2.2. трансмиссионные валы для распределения мощности одного источника к нескольким потребителям;
2.3. коренные валы − валы, несущие на себе рабочие органы исполнительных механизмов (коренные валы станков, несущие на себе обрабатываемую деталь или инструмент называют шпинделями).

Классификация валов и осей (продолжение):
3. Прямые валы по форме исполнения и наружной поверхности −
3.1. гладкие валы имеют одинаковый диаметр по всей длине;
3.2. ступенчатые валы содержат участки, отличающиеся друг от друга диаметрами;
3.3. полые валы снабжены осевым отверстием, простирающимся на большую часть длины вала;
3.4. шлицевые валы по внешней цилиндрической поверхности имеют продольные выступы – шлицы, равномерно расположенные по окружности и предназначенные для передачи моментной нагрузки от или к деталям, непосредственно участвующим в передаче вращающего момента;
3.5. валы, совмещённые с элементами, непосредственно участвующими в передаче вращающего момента (вал-шестерня, вал-червяк).

Конструктивные элементы валов представлены на рис. 9.3.
Рис. 9.3. Основные элементы вала.
С цапфами вала взаимодействуют элементы, обеспечивающие возможность его вращения, удерживающие вал в необходимом для нормальной работы положении и воспринимающие нагрузку со стороны вала.
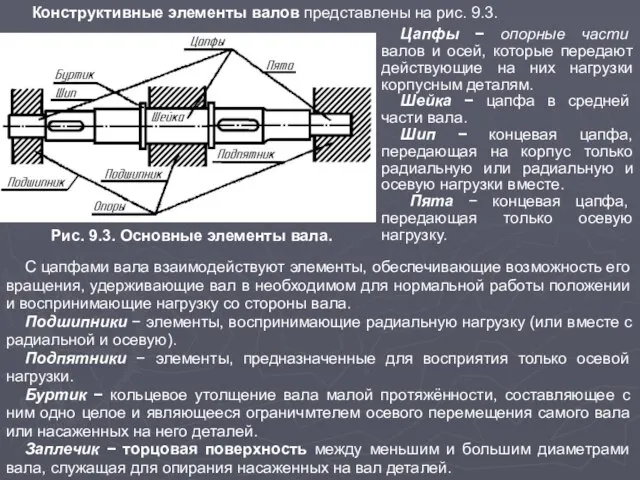
Подшипники − элементы, воспринимающие радиальную нагрузку (или вместе с радиальной и осевую).
Подпятники − элементы, предназначенные для восприятия только осевой нагрузки.
Буртик − кольцевое утолщение вала малой протяжённости, составляющее с ним одно целое и являющееся ограничмтелем осевого перемещения самого вала или насаженных на него деталей.
Заплечик − торцовая поверхность между меньшим и большим диаметрами вала, служащая для опирания насаженных на вал деталей.
Цапфы − опорные части валов и осей, которые передают действующие на них нагрузки корпусным деталям.
Шейка − цапфа в средней части вала.
Шип − концевая цапфа, передающая на корпус только радиальную или радиальную и осевую нагрузки вместе.
Пята − концевая цапфа, передающая только осевую нагрузку.

Галтель − переходная поверхность от цилиндрической части вала к заплечику, выполненная обычно без удаления материала с цилиндрической и торцевой поверхности (рис. 9.4. б, в).
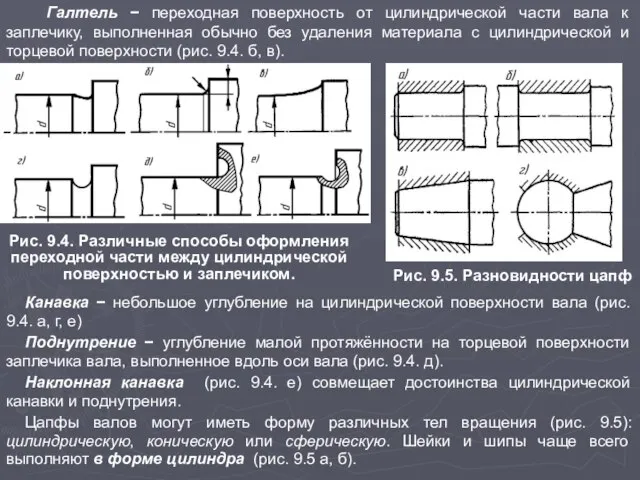
Рис. 9.4. Различные способы оформления переходной части между цилиндрической поверхностью и заплечиком.
Канавка − небольшое углубление на цилиндрической поверхности вала (рис. 9.4. а, г, е)
Поднутрение − углубление малой протяжённости на торцевой поверхности заплечика вала, выполненное вдоль оси вала (рис. 9.4. д).
Наклонная канавка (рис. 9.4. е) совмещает достоинства цилиндрической канавки и поднутрения.
Цапфы валов могут иметь форму различных тел вращения (рис. 9.5): цилиндрическую, коническую или сферическую. Шейки и шипы чаще всего выполняют в форме цилиндра (рис. 9.5 а, б).
Рис. 9.5. Разновидности цапф

Выходные концы валов (рис. 9.1; 9.7) обычно имеют цилиндрическую или коническую форму и снабжаются шпоночными пазами или шлицами для передачи вращающего момента.
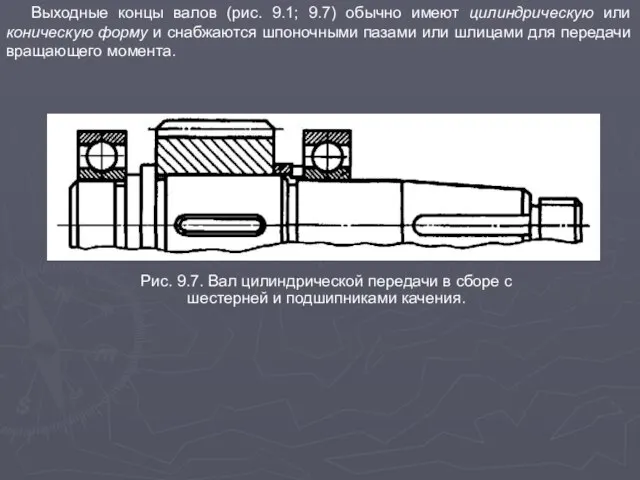
Рис. 9.7. Вал цилиндрической передачи в сборе с шестерней и подшипниками качения.

Материалы для изготовления ВиО, термическая и механическая обработка.
Требования к материалам валов и осей:
1) высокая усталостная прочность (способность противостоять знакопеременным нагрузкам),
2) жесткостью (иметь высокий модуль упругости),
3) хорошая обрабатываемость.
Наиболее полно этим требованиям удовлетворяют углеродистые и легированные стали.
Малонагруженные валы изготавливают из углеродистых сталей Ст5, Ст6.
1. Качественные среднеуглеродистые стали марок 40, 45, 50 используют для валов стационарных машин и механизмов. Заготовку из этих сталей подвергают улучшающей термической обработке (HRCэ ≤ 36) перед механической обработкой. Валы точат на токарном станке, посадочные места и цапфы шлифуют на шлифовальном станке.
2. Среднеуглеродистые легированные стали марок 40Х, 45Х, 40ХН, 40ХНМА, 35ХГСА используют для валов ответственных передач подвижных машин (валы коробок передач гусеничных машин). Улучшающей термообработке (HRCэ ≤ 45) обычно подвергают деталь уже после предварительной токарной обработки. Посадочные поверхности и цапфы окончательно шлифуют на шлифовальных станках.

3. Мало- и среднеуглеродистые легированные стали марок 20Х, 12ХН3А, 18ХГТ, 25ХГТ, 38Х2МЮА идут на валы нагруженных передач, работающих в реверсивном режиме (шлицевые валы коробок передач колёсных машин). Вал, изготовленный с минимальным припуском под окончательную обработку, подвергается поверхностной химико-термической обработке (цементация, азотирование и т.п.), закаливается до высокой поверхностной твердости (HRCэ 55…65). Рабочие поверхности шлицов, посадочные поверхности и поверхности цапф шлифуются после термической обработки с целью получения необходимой точности.

Основными критериями работоспособности валов и вращающихся осей являются усталостная прочность и жёсткость.
При расчете осей и валов их прочность оценивают по коэффициенту запаса усталостной прочности, а жёсткость – величиной прогиба под действием рабочих нагрузок, углом поворота отдельных сечений (чаще всего опорных сечений цапф) в плоскости осевого сечения и углом закручивания поперечных сечений под действием крутящего момента.
Таким образом, основными расчётными нагрузочными факторами яв­ляются крутящие T и изгибающие M моменты. Влияние на прочность вала растягивающих и сжимающих сил само по себе незначительно и обычно не учитывается.
Расчёт вала должен включать три основных этапа: 1) проектировочный расчёт, 2) формирование расчетной схемы и 3) проверочный расчёт. В некоторых случаях к этим трём этапам расчёта добавляются и другие, например, расчёт на колебания (расчёт вибрационной стойкости), расчёт тепловых деформаций, теплостойкости и т.п.
Проектный расчёт валов производят только на статическую прочность по передаваемому крутящему моменту T. При этом расчёте определяется наименьший диаметр вала, а с целью компенсации неучтённых изгибных нагрузок и других факторов, влияющих на прочность вала, принимают заниженные значения допускаемых напряжений [τ]к ≈ (0,025…0,030)⋅σВ.
; (9.1)
Критерии работоспособности и расчет ВиО.

где τк – максимальные касательные напряжения, действующие во внешних волокнах опасного сечения вала; Tк - крутящий момент, передаваемый через это сечение; Wп – полярный момент инерции рассматриваемого сечения.
Для валов, имеющих круговое или кольцевое (для полых валов) поперечное сечение, из (9.1) получаем
; (9.2)
где D – внешний диаметр вала; β = d/D – относительный диаметр осевого отверстия полого вала (d – абсолютное значение диаметра этого отверстия). Для β ≤ 0,5 расчёт полого вала как сплошного даёт погрешность менее 2,5% от диаметра вала, что позволяет рассчитывать толстостенные валы как сплошные (выражение в скобках принять равным 1).
Полученный таким расчётом диаметр вала округляют до ближайшего большего значения из рядов нормальных линейных размеров по ГОСТ 6636-69. Диаметры других ступеней вала и продольные размеры устанавливают из конструктивных соображений в процессе эскизного проектирования механизма.

Формирование расчётной схемы возможно только после полного конструктивного оформления вала на основе проектного расчёта, эскизного проектирования, подбора подшипников и расчёта конструктивных элементов, участвующих в передаче вращающего момента.
При формировании расчётной схемы вал обычно представляют в виде балки, лежащей на опорах (число опор обычно равно числу подшипников), одна из которых считается закреплённой в осевом направлении.
Если вал установлен в корпусе посредством радиальных или сферических подшипников, опору считают расположенной на геометрической оси вала в точке пересечения с поперечной осью симметрии подшипника.
При использовании радиально-упорных подшипников за точку опоры принимают точку продольной геометрической оси вала, лежащую на её пересечении с нормалью к поверхности качения, проведённой через центр тел качения.
Для подшипников скольжения, а также при установке сдвоенных подшипников качения за точку опоры принимают точку, лежащую на оси вращения и расположенную на расстоянии, равном 0,2…0,3 длины подшипника (суммарной длины пары подшипников качения) от его (их) внутренней кромки.
Силы, действующие на вал со стороны ступиц шкивов, шестерён, звёздочек и других элементов, считают приложенными посередине ступицы, если последняя расположена между подшипниками, и на расстоянии 0,25…0,3 длины ступицы со стороны её внутреннего края, при её консольной установке (то есть на конце вала).

Проверочный расчёт валов производится после формирования расчётной схемы и уточнения всех нагрузок, как по величине, так и по направлению. Этот вид расчёта предусматривает проверку вала на статическую прочность по наибольшей возможной кратковременной нагрузке и на усталостную прочность при переменных напряжениях. В последнем случае вычисляется коэффициент фактического запаса прочности в предположительно опасных сечениях, намечаемых предварительно по эпюре моментов с учётом размеров поперечного сечения и зон концентрации напряжений.
На статическую прочность валы рассчитывают по наибольшей возможной кратковременной нагрузке с учётом динамических и ударных воздействий. В этом случае эквивалентное напряжение в наружном волокне вала
; (9.3)
где σи – максимальное напряжение от изгиба; τк – наибольшее напряжение кручения. Поскольку σи = Mи / Wи, а τк = Tк / Wк, где Wи и Wк момент сопротивления вала в опасном сечении изгибу и кручению, соответственно, и после подстановки всех значений в (9.3) получим
. (9.5)

Зная эквивалентные напряжения, можно проверить запас прочности по пределу текучести
, (9.6)
где нормативный запас прочности [n] обычно принимают равным 1,2…1,8.
Проверочный расчёт на сопротивление усталости проводят по максимальной длительно действующей нагрузке без учёта кратковременных пиковых нагрузок (возникающих, например, во время пуска). Для каждого опасного сечения, установленного в соответствии с эпюрами изгибающих и крутящих моментов, определяют расчётный коэффициент запаса прочности S и сравнивают его с допускаемым [S] (обычно принимают [S] = 1,2…2,5) по выражению
; (9.7)
где Sσ и Sτ - коэффициенты запаса прочности по нормальным и касательным напряжениям соответственно:

(9.8)
где σ-1 и τ-1 – пределы выносливости для материала вала при симметричном цикле изгиба и кручения; σа и τа – амплитуды изменения напряжений изгиба и кручения; σm и τm – средние значения за цикл тех же напряжений; ψσ и ψτ − коэффициенты чувствительности материала вала к асимметрии цикла напряжений (ψτ ≈ 0,5⋅ψσ; 0,05≤ψσ≤ 0,2); KσD и KτD – коэффициенты снижения пределов выносливости по изгибу и кручению, определяемые по формулам:
(9.9)
в которых Kσ и Kτ - эффективные коэффициенты концентрации напряжений для данного сечения вала в зависимости от его формы, Kd – коэффициент влияния абсолютных размеров поперечного сечения, KF – коэффициент влияния шероховатости поверхности вала (для посадок с натягом KF ≈ 1), Kv – коэффициент, учитывающий упрочнение поверхности (при отсутствии поверхностного упрочнённого слоя Kv ≈ 1). Перечисленные коэффициенты устанавливаются по справочным данным с учётом материала и конструкции рассчитываемого вала.

Пределы выносливости σ-1 и τ-1 для улучшенных или нормализованных углеродистых и углеродистых легированных сталей с известным пределом прочности σВ, при симметричном цикле изгиба и кручения можно определить по эмпирическим зависимостям
(9.10)
где все значения напряжений в Н/мм2 (МПа).
Амплитудные и медиальные (средние) значения нормальных σа, σm и касательных τа, τm напряжений вычисляют согласно известным выражениям
(9.11)
где σmax и σmin, τmax и τmin – максимальные и минимальные значения нормальных и касательных напряжений в точках наружных волокон опасного сечения вала, которые, в свою очередь, вычисляются по соответствующим формулам сопротивления материалов
(9.12)
Типичными являются такие условия нагружения, когда напряжения от изгиба валов имеют чисто симметричный характер, то есть максимальный и минимальный изгибающие моменты в данном сечении равны по величине и
противоположны по направлению. Для таких условий σa = σmax, а средние напряжения за цикл σm = 0.

Проверочный расчёт валов на жёсткость чаще всего выполняется по нескольким критериям. Наиболее часто при этом виде расчёта определяются:
1) прогиб вала в определённых сечениях (например, под зубчатым или червячным колесом);
2) максимальный прогиб вала;
3) поворот отдельных сечений вала, вызванный его изгибом (чаще всего в местах установки подшипников);
4) закручивание вала под действием рабочих моментов.
Исходя из изложенного, получаем следующие критерии жесткости вала:
прогиб под элементами зацепления – y ≤ [y];
полная стрела прогиба– f ≤ [f];
угол поворота сечения– θ ≤ [θ];
удельный угол закручивания вала– ϕ0 ≤ [ϕ0];
где допустимые значения прогибов и углов составляют:
Предельный прогиб в месте установки зубчатых колёс при модуле зацепления m
цилиндрических − [y] = 0,01m;
конических, гипоидных, глобоидных, червячных − [y] = 0,005m;
полная стрела прогиба − [f] = 3⋅10-4l, где l − полная длина вала;
допустимый удельный угол закручивания вала–0,025 ≤ [ϕ0] ≤ 1,0 градус/м в зависимости от конструкции и назначения вала.
Для осей полный прогиб [f] ≈ (2…3)⋅10-3l, где l − полная длина оси.

Проверку прогиба вала в заданных сечениях наиболее удобно выполнять методом перемножения эпюр Максвелла-Мора (непосредственно выполняемое способом Симпсона или способом Верещагина), согласно которому деформация от изгиба в заданном сечении равна
; (9.13)
где M1(s) - изгибающий момент от единичной фиктивной нагрузки, приложенной в исследуемом сечении; Mи(s) - изгибающий момент от реально действующей нагрузки; E - модуль упругости материала вала I - осевой момент инерции сечений вала; s - текущая координата сечений вдоль оси вала.
Если моменты монотонно изменяются на каждом участке по длине вала, а осевой момент инерции сечений вала I можно считать постоянным по его длине, то выражение (9.13) существенно упрощается.
В этом случае по способу Симпсона величина прогиба может быть подсчитана по следующей формуле:
; (9.14)
в которой m и M - ординаты однородных участков (таких, на которых нет изломов и скачков) эпюр от единичной фиктивной и реальной нагрузок, а индексы "Л", "С" и "Пр" относятся к левому концу, середине и правому концу каждого участка соответственно. Формула Симпсона особенно удобна для определения прогибов валов при линейных эпюрах изгибающих моментов.

А по способу Верещагина при вышеназванных условиях величина прогиба в исследуемом сечении определяется следующим образом:
; (9.15)
в которой A- площади однородных участков эпюр изгибающих моментов, а hc - ординаты второй эпюры под центром тяжести этих площадей.
Расчет валов на колебания. Колебания валов могут быть поперечными (изгибными) и крутильными. Поперечные вызываются наличием несбалансированных масс - маховиков, шкивов, зубчатых колес и т.п. (рис. 9.8). Крутильные колебания возникают вследствие неравномерности вращательного движения валов, связанных с инерционными деталями, механизма.
Рис. 9.8. Схема возникновения
поперечной пульсирующей силы
В простейшем случае, когда вал соединен с одной вращающейся неуравновешенной массой - маховиком (массой и моментом инерции самого вала в этом случае чаще всего можно пренебречь), деформацию вала при вынужденных колебаниях можно представить следующим образом:

. (9.16)
Верхнее равенство относится к изгибным колебаниям, нижнее − к крутильным. В этих равенствах f и ϕ − величина смещения (поперечного или углового) присоединенного маховика; Pа и Ma − возмущающий фактор (сила или момент); m и J − характеристика инерционности (масса и момент инерции маховика) ω0и и ω0к − частоты собственных изгибных и крутильных колебаний системы, соответственно; ωв − частота действия возмущающего фактора. При этом частота собственных колебаний равна корню квадратному из отношения жесткости к характеристике инерции:
. (9.17)
где k - изгибная жесткость вала (величина прогиба от действия единичной поперечной силы), а κ - крутильная жесткость вала (величина угла закручивания от действия единичного крутящего момента). В знаменатель обоих выражений (9.16) входит разность между собственной частотой вала и частотой действия вынуждающего фактора. При совпадении этих двух частот величина деформации устремляется в бесконечность, что эквивалентно разрушению.