Презентация на тему Аксиомы стереометрии 10 класс

Цели:
Изучить аксиомы стереометрии:
- о взаимном расположении точек,
- о взаимном расположении прямых,
- о взаимном расположении плоскостей
в пространстве.
Изучить некоторые следствия из аксиом стереометрии.
Показать применение аксиом к решению задач.
www.konspekturoka.ru

Изучает свойства геометрических фигур на плоскости
Изучает свойства фигур в пространстве
В переводе с греческого слово «геометрия» означает «землемерие»
«гео» – по-гречески земля, «метрео» – мерить
Слово «стереометрия» происходит от греческих слов «стереос» объемный, пространственный, «метрео» – мерить
Изучение нового материала.
www.konspekturoka.ru

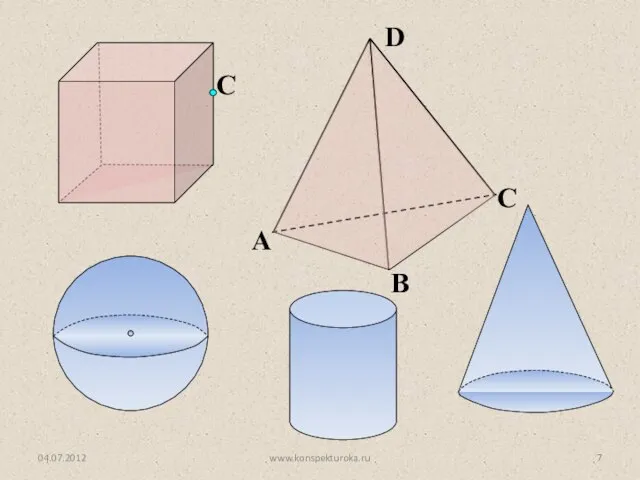
Планиметрия
Стереометрия
Наряду с этими фигурами мы будем рассматривать геометрические тела и их поверхности.
Например, многогранники. Куб, параллелепипед, призма, пирамида.
Тела вращения.
Шар, сфера, цилиндр, конус.
Основные фигуры: точка, прямая
Основные фигуры: точка, прямая, плоскость
Другие фигуры: отрезок, луч, треугольник, квадрат, ромб, параллелограмм, трапеция, прямоугольник, выпуклые и невыпуклые n-угольники, круг, окружность, дуга и др.
Изучение нового материала.
www.konspekturoka.ru

Для обозначение точек используем прописные латинские буквы
Для обозначение прямых используем строчные латинские буквы
Или обозначаем прямую двумя прописными латинскими буквами.
www.konspekturoka.ru

Плоскости будем обозначать греческими буквами.
На рисунках плоскости обозначаются в виде параллелограммов. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.
www.konspekturoka.ru

C
www.konspekturoka.ru

Основные свойства точек, прямых и плоскостей выражены в аксиомах. Из множества аксиом мы сформулируем только три.
А1. Через любые три точки, не лежащие на одной
прямой, проходит плоскость, и притом только одна.
Иллюстрация к аксиоме А1: стеклянная пластинка плотно ляжет на три точки А, В и С, не лежащие на одной прямой.
A
B
C
www.konspekturoka.ru

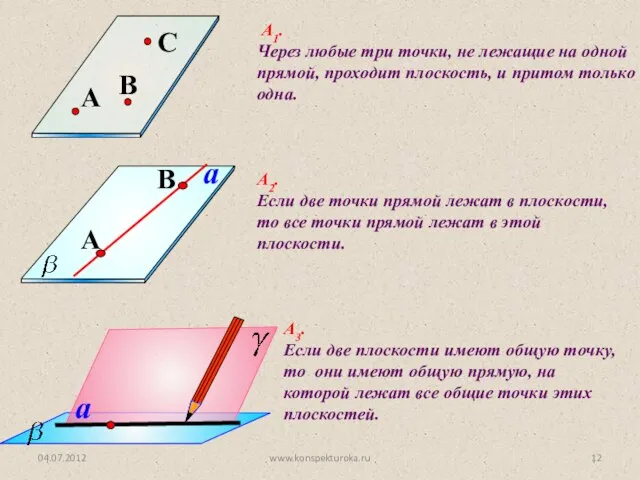
a
А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
A
B
www.konspekturoka.ru

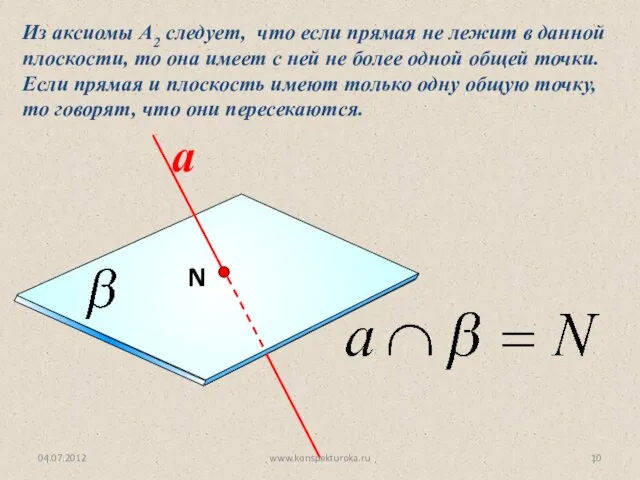
Из аксиомы А2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются.
www.konspekturoka.ru

a
А3. Если две плоскости имеют общую точку, то они
имеют общую прямую, на которой лежат все общие
точки этих плоскостей.
В этом случае говорят, что плоскости пересекаются по прямой.
www.konspekturoka.ru

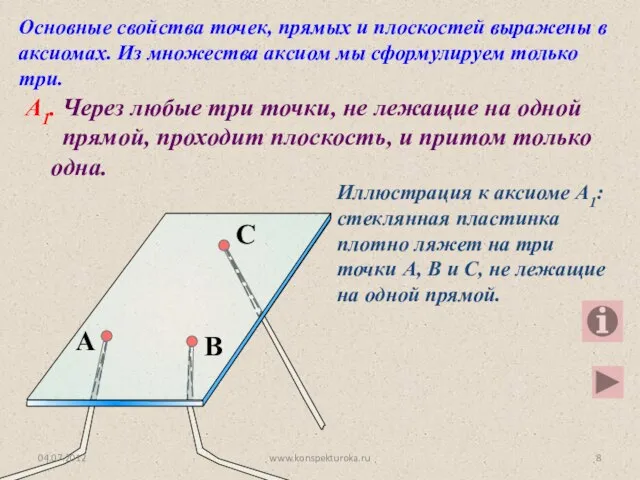
А1.
Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
www.konspekturoka.ru

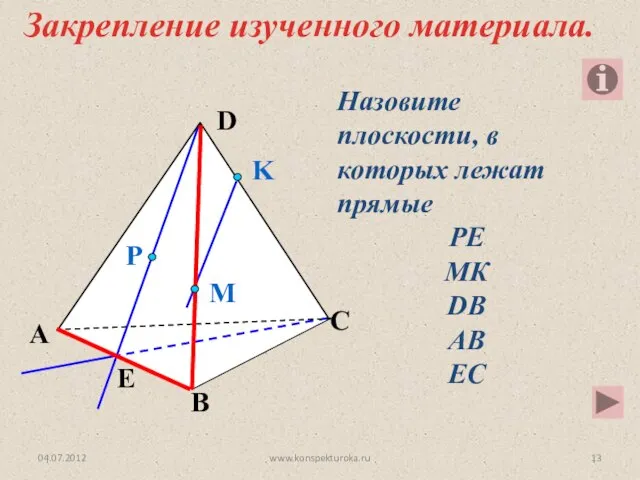
Назовите плоскости, в которых лежат прямые
РЕ
МК
DB
AB
EC
P
E
A
B
C
D
M
K
Закрепление изученного материала.
www.konspekturoka.ru

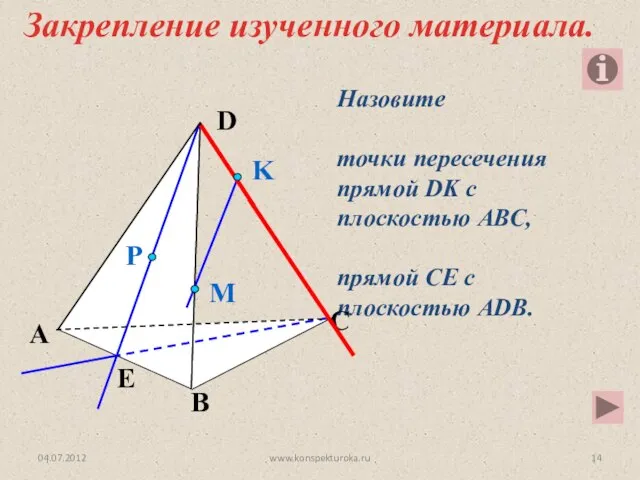
Назовите
точки пересечения прямой DK с плоскостью АВС,
прямой СЕ с плоскостью АDB.
P
E
A
B
C
D
M
K
Закрепление изученного материала.
www.konspekturoka.ru

Назовите точки, лежащие в плоскостях АDB и DBC
P
E
A
B
C
D
M
K
Закрепление изученного материала.
www.konspekturoka.ru

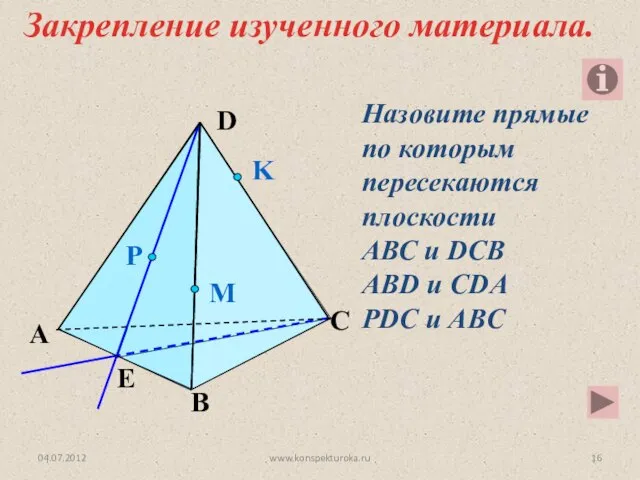
Назовите прямые по которым пересекаются плоскости
АВС и DCB
ABD и CDA
PDC и ABC
P
E
A
B
C
D
M
K
Закрепление изученного материала.
www.konspekturoka.ru