Содержание
- 2. Алгебра и логика Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами: А = {Аристотель -
- 3. Алгебра и логика Составные высказывания на естественном языке образуются с помощью союзов: Солнце в зените И
- 4. Солнце в зените И тени нет. Логическая операция КОНЪЮНКЦИЯ (логическое умножение): в естественном языке соответствует союзу
- 5. Мы пойдём в кино ИЛИ на дискотеку. Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение): в естественном языке соответствует
- 6. НЕВЕРНО, что Солнце движется вокруг Земли. Логическая операция ИНВЕРСИЯ (отрицание): в естественном языке соответствует словам неверно,
- 7. ЕСЛИ сумма цифр числа делится на 3, ТО число делится на 3 Логическая операция ИМПЛИКАЦИЯ (логическое
- 8. Число 15 делится на 3 ТОГДА И ТОЛЬКО ТОГДА, когда сумма цифр числа 15 делится на
- 10. Скачать презентацию







 Заболевание височно-нижнечелюстного сустава
Заболевание височно-нижнечелюстного сустава  Конфликтный треугольник: семья-ребенок-образовательное учреждение. Детская агрессия
Конфликтный треугольник: семья-ребенок-образовательное учреждение. Детская агрессия кольцово
кольцово Проблемы преемственности начального и основного (общего) образования
Проблемы преемственности начального и основного (общего) образования Проектная деятельность
Проектная деятельность Власть. Структурная и ситуационная власть
Власть. Структурная и ситуационная власть Свечникова В.В. правоведение тема 2 презентация
Свечникова В.В. правоведение тема 2 презентация Майолика. Гутные изделия. Ковка
Майолика. Гутные изделия. Ковка Saint Petersburg state University
Saint Petersburg state University 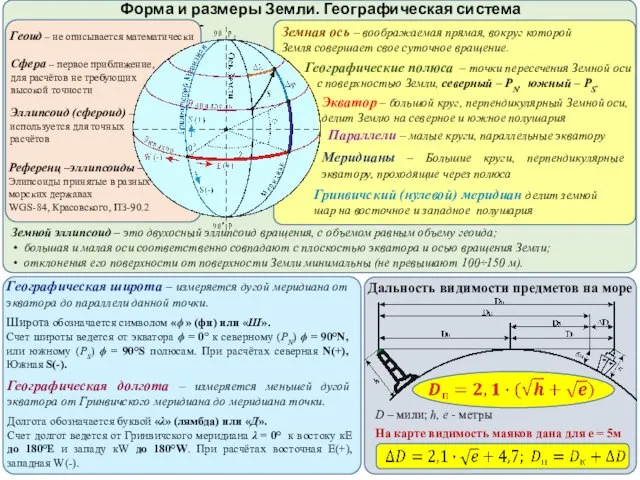 Форма и размеры Земли
Форма и размеры Земли Поздравление крестной жениха
Поздравление крестной жениха Гендерные аспекты образования и рынка труда
Гендерные аспекты образования и рынка труда Геометрия на службе у архитектуры
Геометрия на службе у архитектуры Психология двигательно-волевой сферы психической деятельности
Психология двигательно-волевой сферы психической деятельности Команда звёздочки
Команда звёздочки История семейного образования в СанктПетербурге
История семейного образования в СанктПетербурге Русский пейзаж в поэзии и живописи
Русский пейзаж в поэзии и живописи Физическая культура в период самоизоляции студентов педагогического вуза
Физическая культура в период самоизоляции студентов педагогического вуза Заповедники России
Заповедники России Презентация на тему Прощание с 1 классом
Презентация на тему Прощание с 1 классом Клёш и фалды
Клёш и фалды Быть нормальным
Быть нормальным Основные формы рельефа Алтайского края
Основные формы рельефа Алтайского края  Проект: Комплексное сопровождение покупки страховой компании
Проект: Комплексное сопровождение покупки страховой компании Сделка. Предпринимательская деятельность
Сделка. Предпринимательская деятельность русский язык - язык международного общения
русский язык - язык международного общения Условия признания и исполнения иностранных судебных решений
Условия признания и исполнения иностранных судебных решений