Содержание
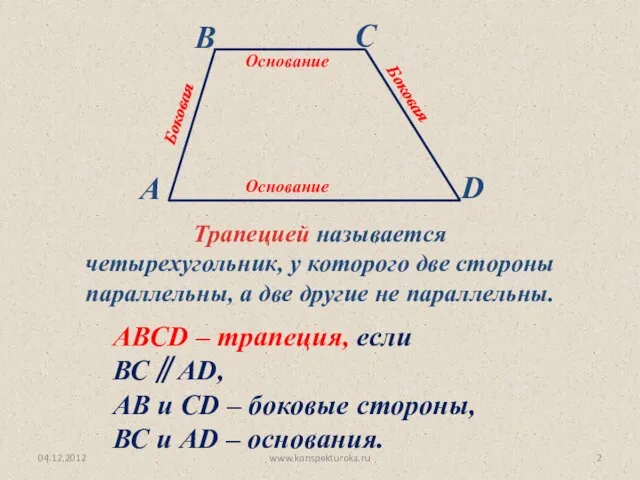
- 2. 04.12.2012 www.konspekturoka.ru Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны. АВСD
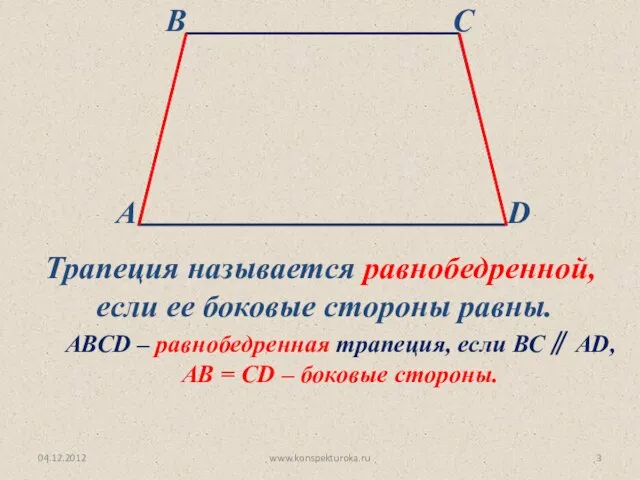
- 3. 04.12.2012 www.konspekturoka.ru Трапеция называется равнобедренной, если ее боковые стороны равны. АВСD – равнобедренная трапеция, если ВС∥
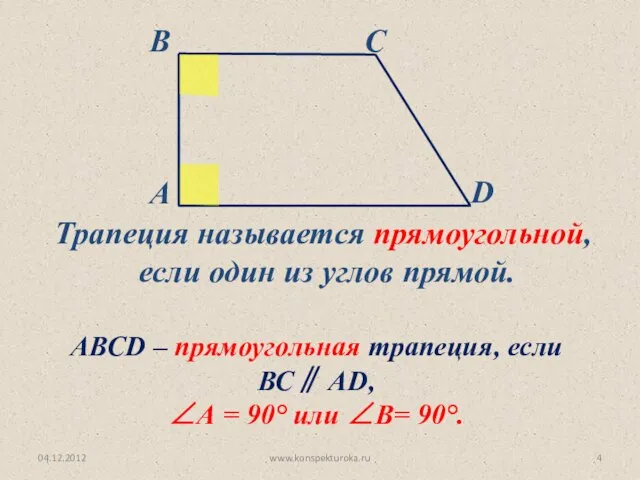
- 4. 04.12.2012 www.konspekturoka.ru Трапеция называется прямоугольной, если один из углов прямой. АВСD – прямоугольная трапеция, если ВС∥
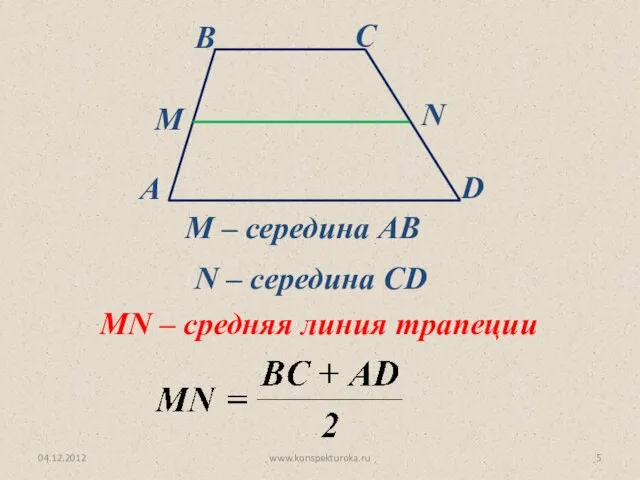
- 5. 04.12.2012 www.konspekturoka.ru М – середина АВ N – середина CD MN – средняя линия трапеции
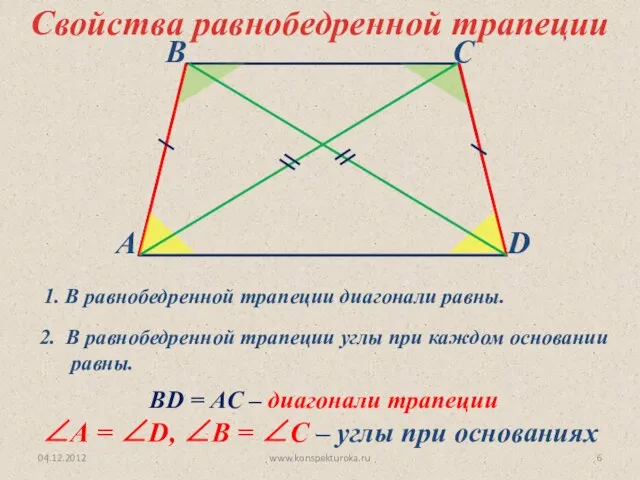
- 6. 04.12.2012 www.konspekturoka.ru ВD = AC – диагонали трапеции ∠А = ∠D, ∠В = ∠С – углы
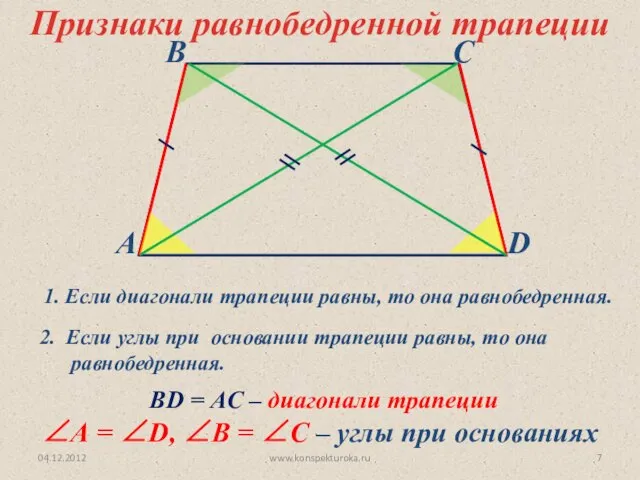
- 7. 04.12.2012 www.konspekturoka.ru ВD = AC – диагонали трапеции ∠А = ∠D, ∠В = ∠С – углы
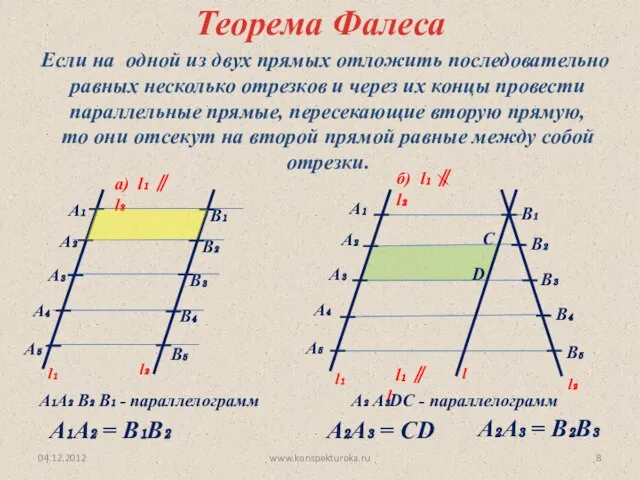
- 8. 04.12.2012 www.konspekturoka.ru Теорема Фалеса Если на одной из двух прямых отложить последовательно равных несколько отрезков и
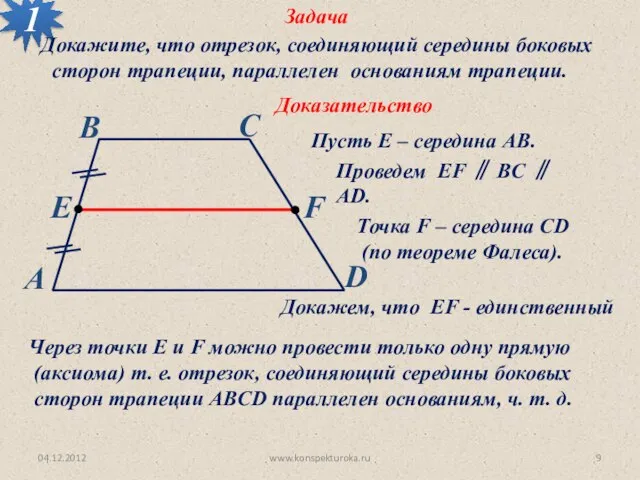
- 9. 04.12.2012 www.konspekturoka.ru Задача 1 Доказательство Докажите, что отрезок, соединяющий середины боковых сторон трапеции, параллелен основаниям трапеции.
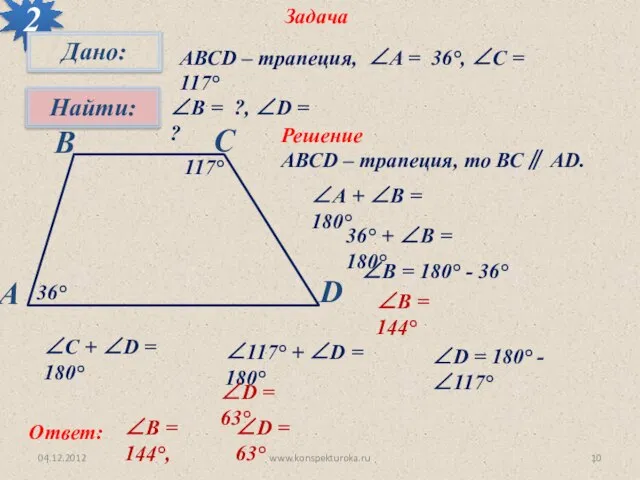
- 10. 04.12.2012 www.konspekturoka.ru Задача 2 АВСD – трапеция, ∠A = 36°, ∠C = 117° ∠В = ?,
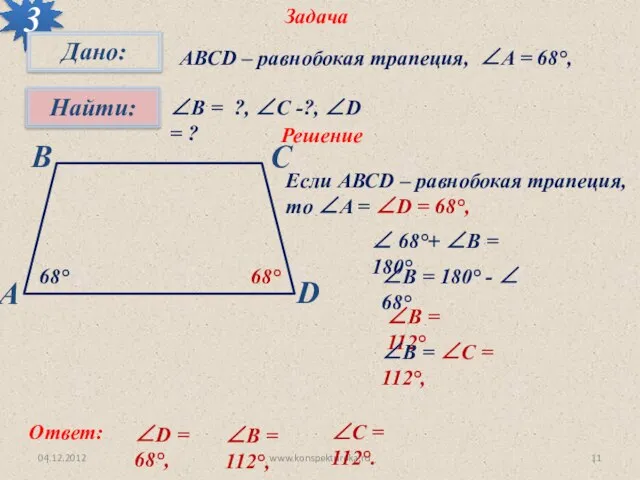
- 11. 04.12.2012 www.konspekturoka.ru Задача 3 АВСD – равнобокая трапеция, ∠A = 68°, ∠В = ?, ∠С -?,
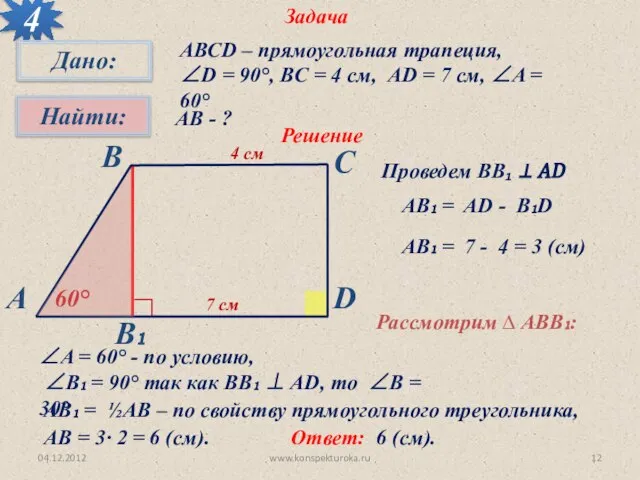
- 12. 04.12.2012 www.konspekturoka.ru Задача 4 АВСD – прямоугольная трапеция, ∠D = 90°, BC = 4 см, AD
- 14. Скачать презентацию
 Технология приема порожних и груженых вагонов к перевозке в цифровом формате Цифровой приемосдатчик
Технология приема порожних и груженых вагонов к перевозке в цифровом формате Цифровой приемосдатчик Логарифмы. Логарифмическая функция
Логарифмы. Логарифмическая функция Экологическое поле
Экологическое поле Моя семья в истории страны
Моя семья в истории страны Пусть промоушн
Пусть промоушн Ситник Светлана Михайловна Зав. отделом справочно-информационной работы ЦНБ НАН Беларуси, председатель Комитета по библиографиче
Ситник Светлана Михайловна Зав. отделом справочно-информационной работы ЦНБ НАН Беларуси, председатель Комитета по библиографиче Домашние животные. Деревенский двор
Домашние животные. Деревенский двор География религий
География религий Структурированные типы данных
Структурированные типы данных  Legal profession
Legal profession  Системы дистанционного банковского обслуживания «Интернет-Банк» и «Мобильный банк
Системы дистанционного банковского обслуживания «Интернет-Банк» и «Мобильный банк Ц у н а м и
Ц у н а м и Be mine!
Be mine! Технологии ! (1)
Технологии ! (1) UML_osnovy (1)
UML_osnovy (1) Как кодируется изображение?
Как кодируется изображение? Город Санкт - Петербург
Город Санкт - Петербург  Dzień Pluszowego Misia
Dzień Pluszowego Misia Узбекистан
Узбекистан Поговорим о школьном питании
Поговорим о школьном питании Укажите метафору.
Укажите метафору. Презентация на тему Охрана Труда В ДОУ
Презентация на тему Охрана Труда В ДОУ Innovative Teachers Network in Russia www.it-n.ru home Предметы Цель и задачи Краткое описание Экономика, география, математика, право, информатика и ИКТ,
Innovative Teachers Network in Russia www.it-n.ru home Предметы Цель и задачи Краткое описание Экономика, география, математика, право, информатика и ИКТ, Ручные помпы
Ручные помпы Презентация на тему Интегрированный подход в оздоровлении детей дошкольного возраста в условиях внедрения ФГТ
Презентация на тему Интегрированный подход в оздоровлении детей дошкольного возраста в условиях внедрения ФГТ Презентация на тему Организация и содержание физминутки на уроке
Презентация на тему Организация и содержание физминутки на уроке Разовая закупка. Аукцион в электронной форме
Разовая закупка. Аукцион в электронной форме Деловая переписка
Деловая переписка