Воздушный режим здания. Лекция12

СОДЕРЖАНИЕ
Общие сведения
Состояние воздушного режима здания при тепловом и ветровом давлении Теплопередача через ограждение при наличии инфильтрации
Расчет воздушного режима наружных ограждений

СОСТОЯНИЕ ВОЗДУШНОГО РЕЖИМА ЗДАНИЯ ПРИ ТЕПЛОВОМ И ВЕТРОВОМ ДАВЛЕНИИ
Состояние воздушного режима здания при тепловом и ветровом давлении необходимо знать для того чтобы рассчитать величину перепада давления ΔР на поверхностях ограждения, которая оказывает влияние на количество инфильтрирующегося воздуха.
а) Рассмотрим определение величины теплового давления.
В зимнее время воздух в отапливаемых помещениях имеет более высокую температуру, чем наружный воздух tв > tн . При этом наружный воздух будет иметь больший объемный вес, чем воздух в здании γн > γв .
Разность объемных весов воздуха и создаёт разности его давлений.
На рис. 2 показано отапливаемое помещение с 2МЯ наружными стенами. Если в таком здании пол и потолок будут воздухонепроницаемыми, то через нижнюю половину воздух будет проникать в здание, а через верхнюю уходить. Величина давления относительно нейтральной зоны в некотором сечении h будет определяться по уравнению:
Рi = h⋅(γн− γв), (1) .

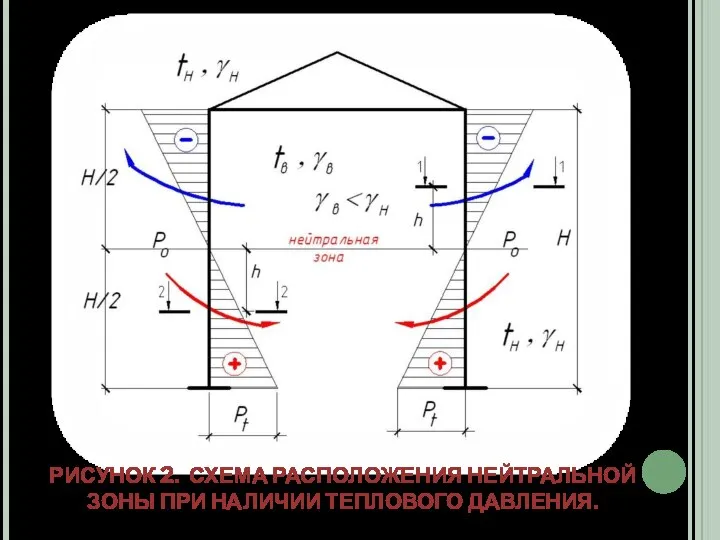
РИСУНОК 2. СХЕМА РАСПОЛОЖЕНИЯ НЕЙТРАЛЬНОЙ ЗОНЫ ПРИ НАЛИЧИИ ТЕПЛОВОГО ДАВЛЕНИЯ.

На положение нейтральной зоны оказывает влияние работа систем вентиляции.
При положительном дисбалансе (П>В) нейтральная зона повышается; при отрицательном (В>П) – понижается.
Если нейтральная зона находится в середине помещения, то величина теплового давления определяется по уравнению:
Рi = H/2⋅(γн− γв), (2) .
где γн , γв - удельный вес наружного и внутреннего воздуха;
h - расстояние от нейтральной поверхности, м;
H - высота здания, м.
Из уравнений (1) и (2) видно, что величина теплового давления будет возрастать с увеличением высоты здания и с повышением разности температур tв > tн .
б) Рассмотрим определение величины ветрового давления.
Полное давление ветра, оказываемое им на плоскость, перпендикулярную его направлению, определяется по формуле:
с = (ν 2⋅γн )/2 , (3) .

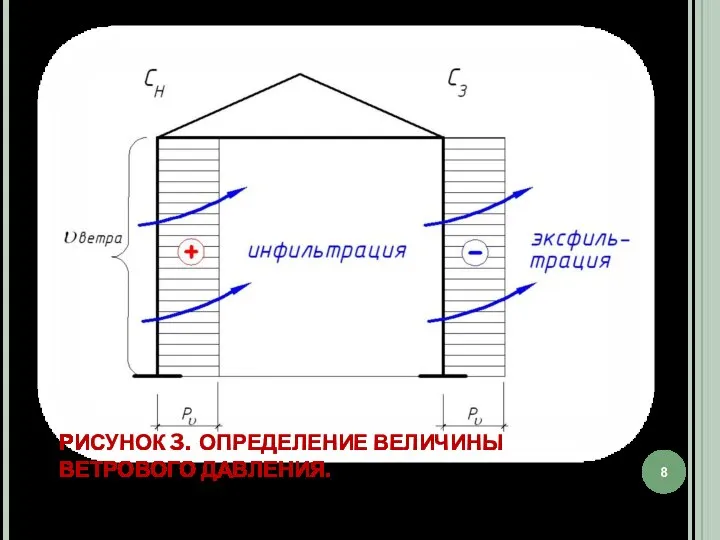
РИСУНОК 3. ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ ВЕТРОВОГО ДАВЛЕНИЯ.

Следует отметить, что давление ветра на наружное ограждение будет составлять только некоторую часть от его полного давления, характеризуемого аэродинамическими коэффициентами сН и с3. Тогда ветровое давление можно будет определить по уравнению:
(4) .
Практически в природе встречаются условия, когда одновременно
νВЕТРА > 0 , и tв > tн , в этом случае необходимо определить общее давление:
ветровое и тепловое. Для этого применим принцип независимости действия сил. Тогда эпюра совместных давлений примет вид:
(5) .
Для удобства расчетов воздушного режима здания, оказывается удобным построить эпюры давлений так, чтобы по всему контуру здания они были со знаком «+».

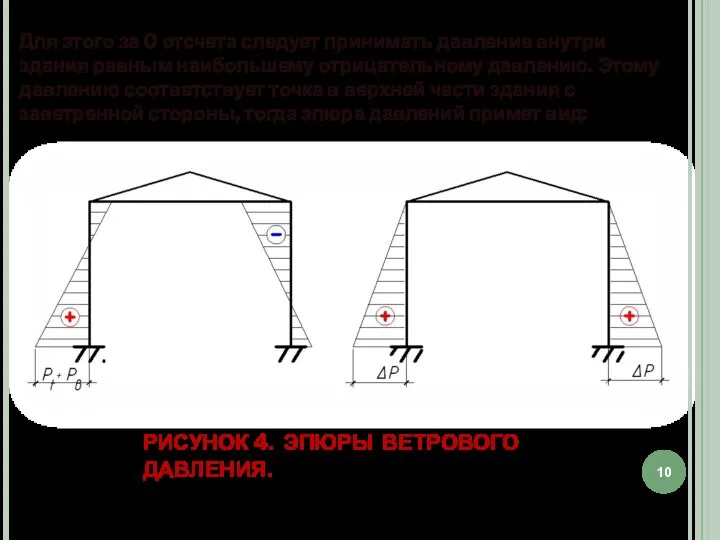
Для этого за 0 отсчета следует принимать давление внутри здания равным наибольшему отрицательному давлению. Этому давлению соответствует точка в верхней части здания с заветренной стороны, тогда эпюра давлений примет вид:
РИСУНОК 4. ЭПЮРЫ ВЕТРОВОГО ДАВЛЕНИЯ.

Величина перепада давлений определяется по уравнению:
(6) .
сН = 0,8; и с3= -0,4.
ΔР = h⋅(γн− γв)+0,3ν 2⋅γн , (7) .
Уравнение (7) применяется для расчета воздушного режима здания, а для расчета теплопотерь с учетом инфильтрации применяется уравнение с учетом влияния на величину ΔР работы систем вентиляции:
ΔР = (H- h)⋅(γн− γв)+0,5(ν 2/2)⋅γн ⋅(сн− сЗ) ⋅kн- РH ; (8)
где (H- h)⋅(γн− γв) - тепловое давление;.
0,5(ν 2/2)⋅γн ⋅(сн− сЗ) ⋅kн - ветровое давление;
Рн - вентиляционное давление.
Из изложенного следует, что при расчете воздушного режима необходимо иметь в виду наличие инфильтрации, как с наветренной, так и с заветренной стороны.

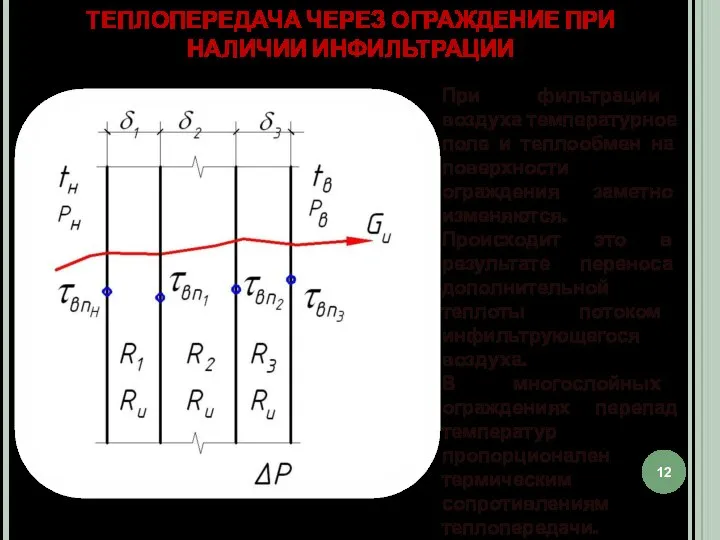
ТЕПЛОПЕРЕДАЧА ЧЕРЕЗ ОГРАЖДЕНИЕ ПРИ НАЛИЧИИ ИНФИЛЬТРАЦИИ
При фильтрации воздуха температурное поле и теплообмен на поверхности ограждения заметно изменяются.
Происходит это в результате переноса дополнительной теплоты потоком инфильтрующегося воздуха.
В многослойных ограждениях перепад температур пропорционален термическим сопротивлениям теплопередачи.

При наличии инфильтрации, можем записать:
(10).
Тогда дифференциальное уравнение одномерного температурного поля при стационарных условиях имеет вид:
(∂2t )/(∂R2) = 0. (9).
Преобразовывая уравнение (10) и решив его относительно τвп(i), получим распределение температуры на внутренней поверхности любого слоя, можно определить:
(11).
где tн , tв - расчетные температуры наружного и внутреннего воздуха, °С;.
e - основание ln;
cв - теплоёмкость воздуха, кДж/кг°С;
Gu - количество инфильтрирующегося воздуха, кг/г ;

Gu - количество инфильтрирующегося воздуха, кг/г ;
R0Ф – сопротивление теплопередаче всего ограждения, м2°С/Вт ;
∑Rni – термическое сопротивление теплопередаче слоев начиная от наружного воздуха в помещении, м2°С/Вт.
Например :
Данное уравнение справедливо в случае инфильтрации, а при эксфильтрации Gu берется со знаком «-».
При отсутствии инфильтрации:
(12).

Анализируя уравнение (11) и (12) видим, что τВП при инфильтрации ниже, чем при ее отсутствии. Фильтрация воздуха также оказывает влияние и на к теплопередачи, которая определяется по формуле:
(13) .
При отсутствии фильтрации:
k = 1/R0Ф, (6), анализ показывает, что ku>k, следовательно это
приводит к увеличению тепловой мощности систем В и КВ.
Изложенное выше требует осуществлять проверку ограждений воздухопроницанию.

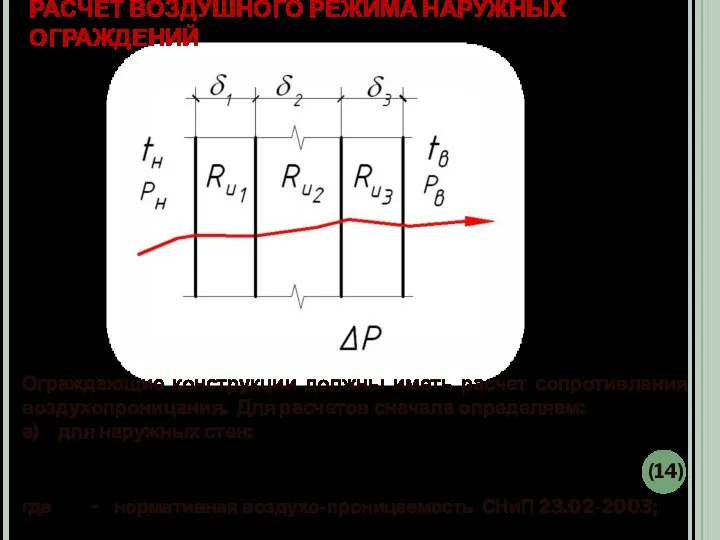
РАСЧЕТ ВОЗДУШНОГО РЕЖИМА НАРУЖНЫХ ОГРАЖДЕНИЙ
Ограждающие конструкции должны иметь расчет сопротивления воздухопроницания. Для расчетов сначала определяем:
а) для наружных стен:
Ruтр =ΔР/Gu , (14) .
где Gu - нормативная воздухо-проницаемость СНиП 23.02-2003;

б) для окон и балконных дверей:
(15 ) .
где ΔР0 - разность давлений воздуха на противоположных поверхностях при испытании на воздухопроницаемость ΔР = 10 Па.
Для оценки воздухопроницаемости наружных ограждений, необходимо определить фактическое сопротивление воздухопроницанию :
Ruф = Ru1+Ru2+Ru3+...+Run . (16) .
Ограждение будет отвечать требованиям воздухопроницания если выполняется условие :
Ruф ≥ Ruтр . (17).