Содержание
- 2. §§ Распространение ЭМВ 02 При колебательном движении зарядов (периодическом изменении токов) происходит перемещение электрической и магнитной
- 3. 03 Возникшая волна, распространяясь от источника колебаний, охватывает все новые и новые области пространства. Поверхность, разделяющая
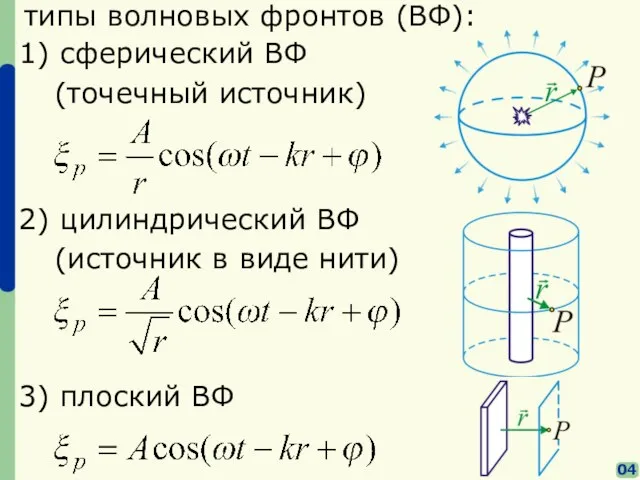
- 4. типы волновых фронтов (ВФ): 1) сферический ВФ (точечный источник) 2) цилиндрический ВФ (источник в виде нити)
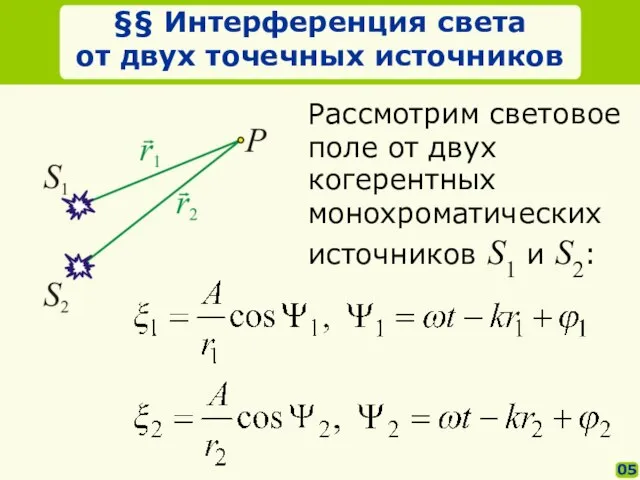
- 5. §§ Интерференция света от двух точечных источников 05 Рассмотрим световое поле от двух когерентных монохроматических источников
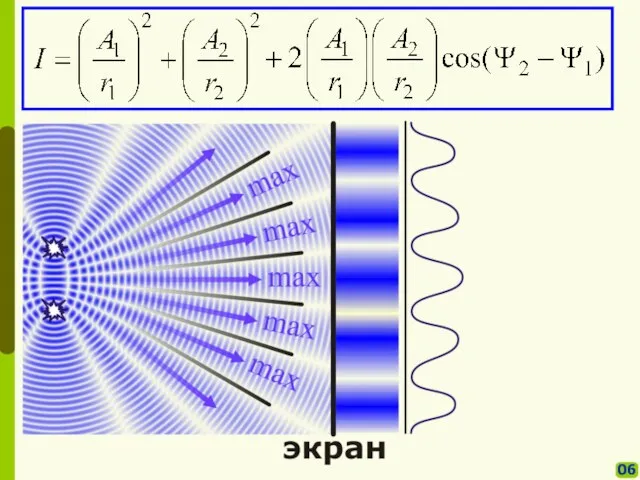
- 6. 06
- 7. §§ Принцип Гюйгенса-Френеля процесс распространения волн в неоднородной среде. дифракция – носят название явлений дифракции. Явления,
- 8. 14 (совокупность поверхностей и диафрагм) Распространение света – волновой процесс. С помощью уравнений Максвелла можно решать
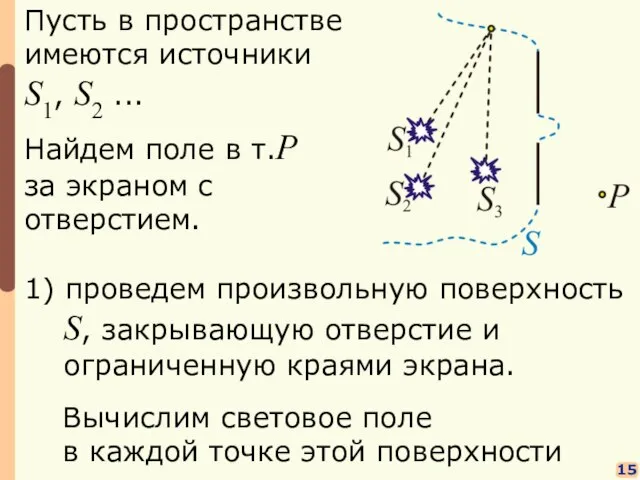
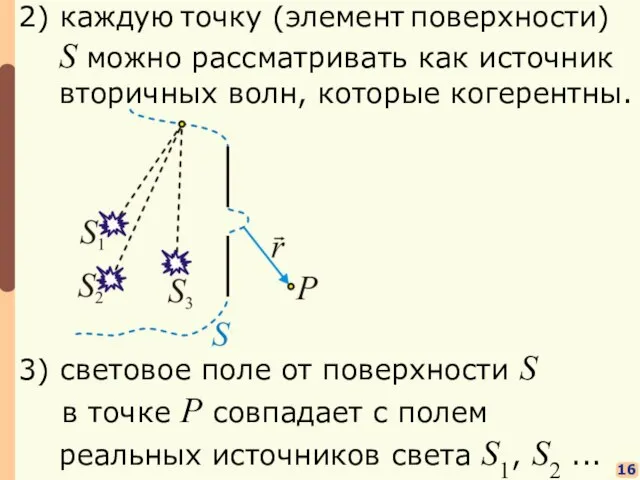
- 9. 15 Пусть в пространстве имеются источники S1, S2 ... Найдем поле в т.P за экраном с
- 10. 16 3) световое поле от поверхности S в точке P совпадает с полем реальных источников света
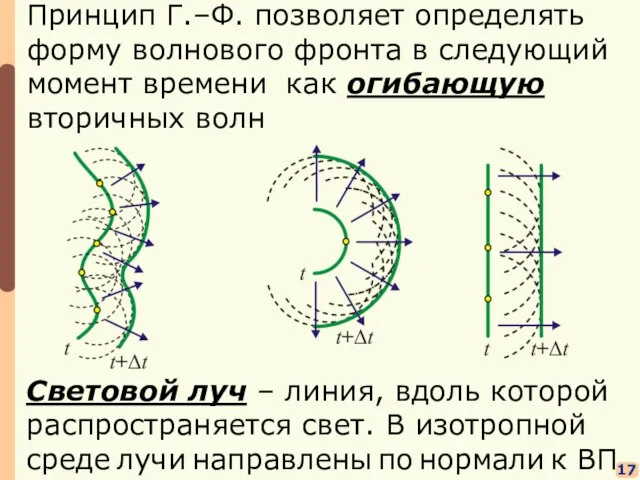
- 11. 17 Принцип Г.–Ф. позволяет определять форму волнового фронта в следующий момент времени как огибающую вторичных волн
- 12. Замечаниe 1: 18 из принципа Г.–Ф. следует закон отражения и преломления света Из принципа также следует
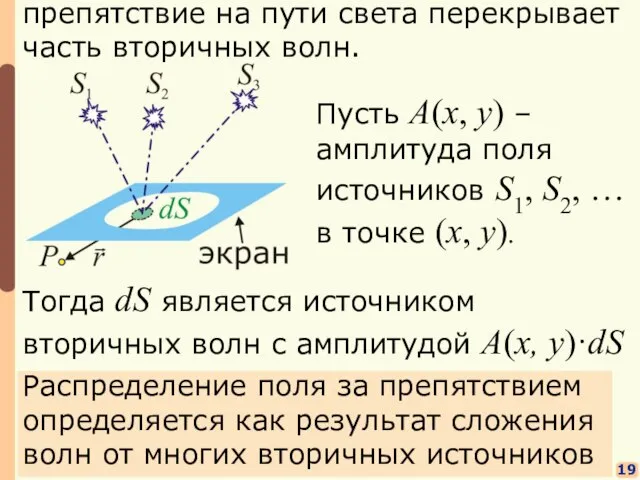
- 13. 19 препятствие на пути света перекрывает часть вторичных волн. Распределение поля за препятствием определяется как результат
- 14. 20 В точке наблюдения: Результирующее поле в т.P: – Ландау Л.Д., Лифшиц Е.М. «Теория поля», стр.
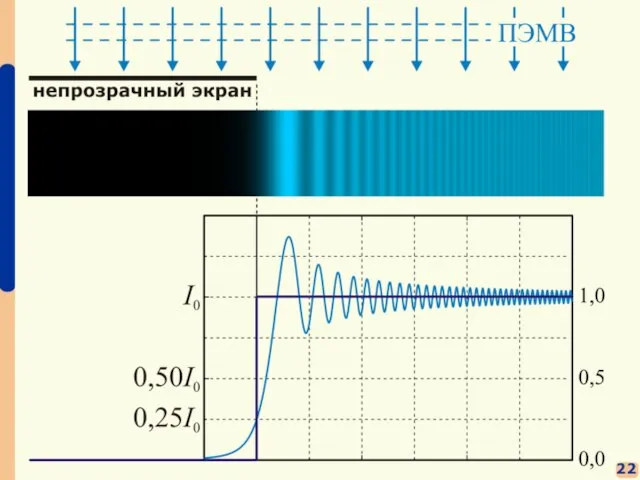
- 15. §§ Дифракция света на полубесконечном экране 21 падает ПЭМВ: A(x, y) = const область экрана: x
- 16. 22
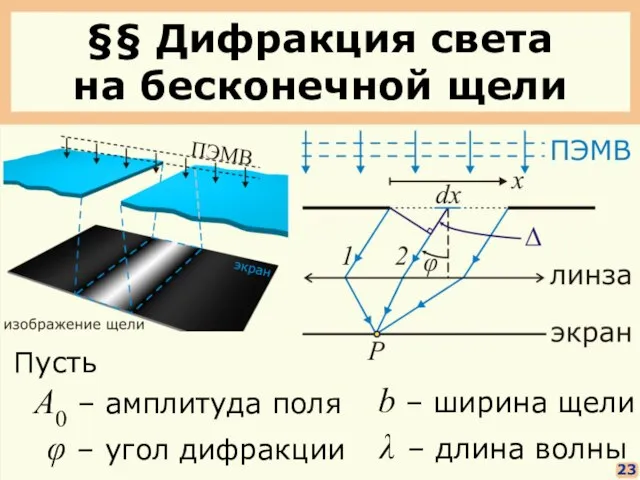
- 17. §§ Дифракция света на бесконечной щели 23 Пусть A0 – амплитуда поля φ – угол дифракции
- 18. 24 Поле элемента dx, находящегося на расстоянии x от края щели: Суммарное поле от всей щели:
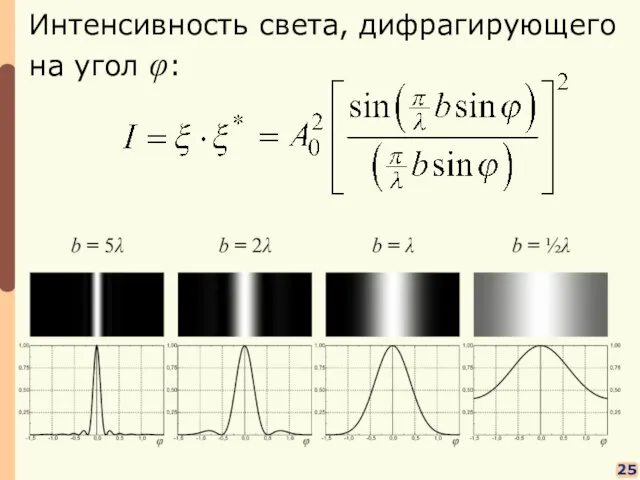
- 19. 25 Интенсивность света, дифрагирующего на угол φ:
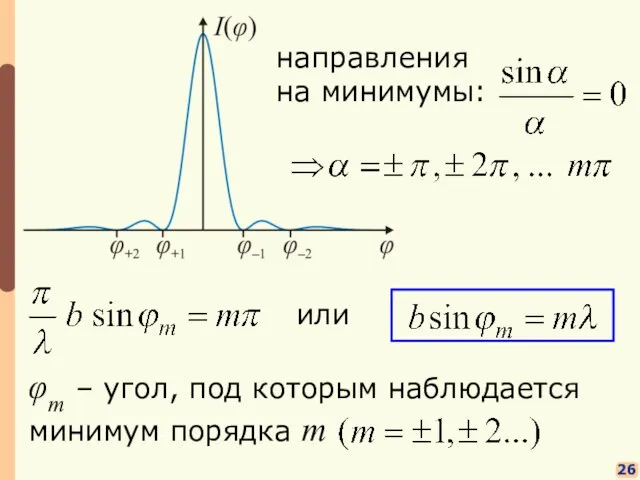
- 20. φm – угол, под которым наблюдается минимум порядка m 26 направления на минимумы: или
- 21. Основные выводы: 27 т.к. sinφm ≤ 1, то наблюдается конечное число min (темных полос); 2) при
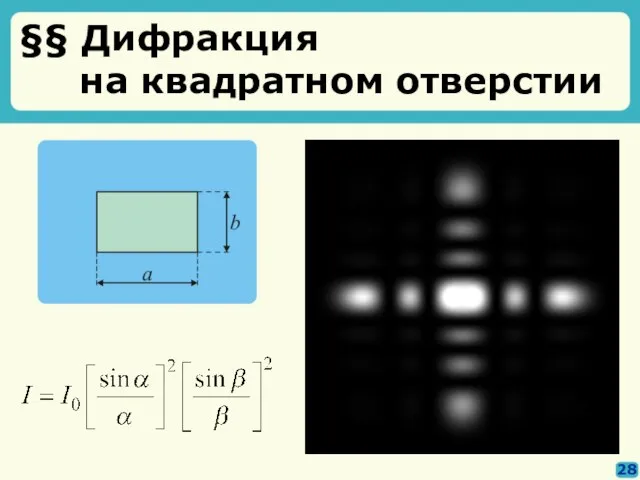
- 22. §§ Дифракция на квадратном отверстии 28
- 23. §§ Дифракция на круглом отверстии 29
- 24. §§ Дифракционная решетка 30 Расстояние между щелями d – называется постоянной (периодом) решетки. это совокупность большого
- 25. 31 Пусть щели – маленькие, тогда они являются источниками вторичных волн с цилиндрическим ВФ. – разность
- 26. 32 условие наблюдения главных дифракционных максимумов при дифракции на решетке – номер главного максимума Точное распределение
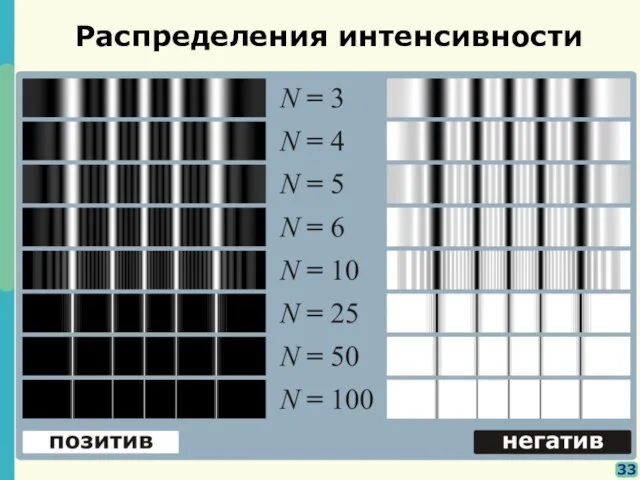
- 27. Распределения интенсивности 33
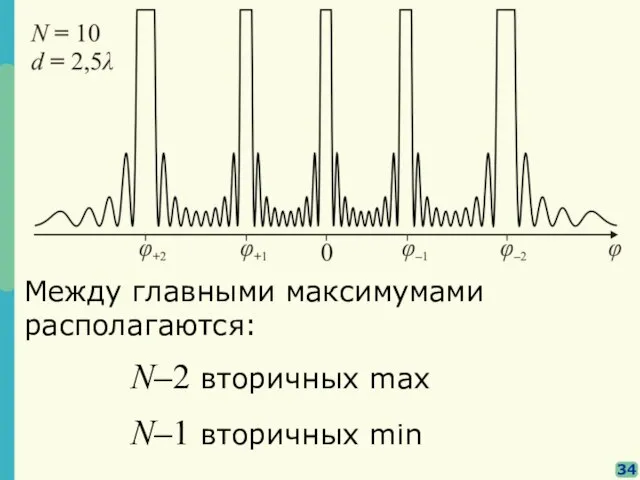
- 28. 34 Между главными максимумами располагаются: N–2 вторичных max N–1 вторичных min
- 29. §§ Дифракционная решетка как спектральный прибор Если в составе падающего излучения присутствуют две спектральные линии λ1
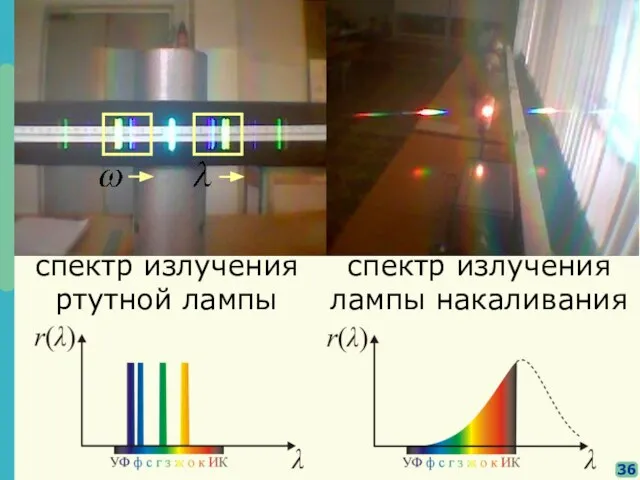
- 30. 36 спектр излучения ртутной лампы спектр излучения лампы накаливания
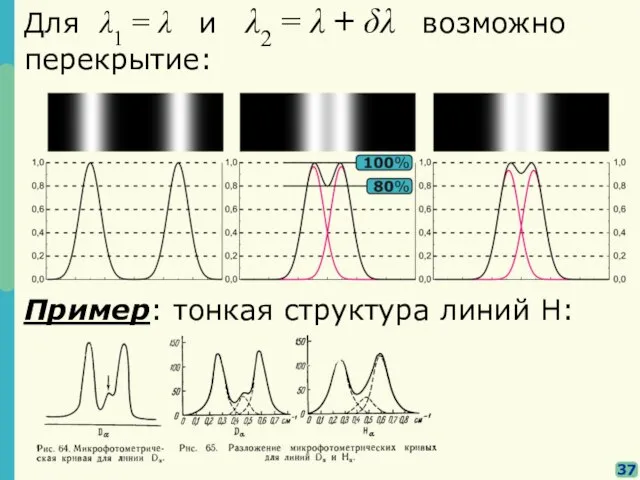
- 31. 37 Для λ1 = λ и λ2 = λ + δλ возможно перекрытие: Пример: тонкая структура
- 32. 38 В этом случае минимум составляет около 80% от значения в максимуме. δλ, соответствующее этому критерию,
- 34. Скачать презентацию







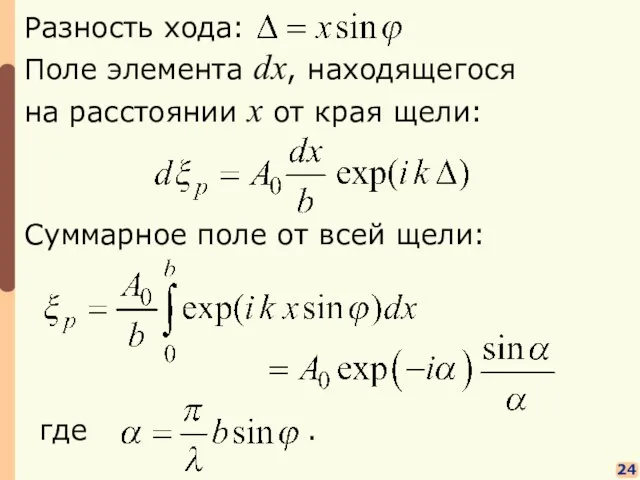







 КАБИНЕТФАКТОЛОГИИ И АНАЛИЗА ДАННЫХ ПО ПРЕДВИДЕНИЮ(www.chronos.msu.ru/cabinets/predvidenie)С.А.Кравченко (www.skravchenko.ru)Москва30 ноября 2010 г.
КАБИНЕТФАКТОЛОГИИ И АНАЛИЗА ДАННЫХ ПО ПРЕДВИДЕНИЮ(www.chronos.msu.ru/cabinets/predvidenie)С.А.Кравченко (www.skravchenko.ru)Москва30 ноября 2010 г. Значение нейронаук для специальной педагогики и психологии
Значение нейронаук для специальной педагогики и психологии Фотографии
Фотографии Антивирусы TrustPort
Антивирусы TrustPort ВПК
ВПК florists department
florists department Основные теги HTML
Основные теги HTML Презентация на тему НАСЕЛЕНИЕ ЗЕМЛИ
Презентация на тему НАСЕЛЕНИЕ ЗЕМЛИ  Формирование толерантности у школьников
Формирование толерантности у школьников Терапевтическая локализация
Терапевтическая локализация  Города-Герои
Города-Герои Бесконтактный велогенератор
Бесконтактный велогенератор Тема 7 (2)
Тема 7 (2) Безграничное пространство сцены
Безграничное пространство сцены Тест на развития когнитивных функций головного мозга. Анаграммы
Тест на развития когнитивных функций головного мозга. Анаграммы Ресурсный центр ядерной медицины СПбГУ Перспективы развития исследований в области медицины и биологии
Ресурсный центр ядерной медицины СПбГУ Перспективы развития исследований в области медицины и биологии УРОВНИ ОРГАНИЗАЦИИ ЖИЗНИНА ЗЕМЛЕ
УРОВНИ ОРГАНИЗАЦИИ ЖИЗНИНА ЗЕМЛЕ Artrologia
Artrologia 23 февраля
23 февраля Горецкий В.Г. Азбука. Учебник: 1 класс: В 2ч Горецкий В.Г., Федосова Н.А, Прописи к "Русской азбуке" 1,2,3,4.
Горецкий В.Г. Азбука. Учебник: 1 класс: В 2ч Горецкий В.Г., Федосова Н.А, Прописи к "Русской азбуке" 1,2,3,4. Силы. Сила тяжести
Силы. Сила тяжести "Жизнь или никотин"
"Жизнь или никотин" Страна фараонов Египет
Страна фараонов Египет Системы урегулирования убытка и контроля расчетов страхового возмещения центральными офисами страховых компаний.
Системы урегулирования убытка и контроля расчетов страхового возмещения центральными офисами страховых компаний. Формирование межкультурной компетенции обучающихся в процессе анализа текстов современных англоязычных СМИ
Формирование межкультурной компетенции обучающихся в процессе анализа текстов современных англоязычных СМИ КВН
КВН Самоконтроль в процессе занятий физкультурой и спортом. Пульс (занятие 9)
Самоконтроль в процессе занятий физкультурой и спортом. Пульс (занятие 9) Предзаказы на 8 марта. Шашлычная
Предзаказы на 8 марта. Шашлычная