Презентация на тему Динамика материальной точки. Работа и энергия

2. Динамика материальной точки
«Всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние».
2.1. Законы Ньютона
Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью.
Первый закон Ньютона выполняется только в инерциальных системах отсчета.
Инерциальная система отсчета – это система, относительно которой материальная точка, свободная от внешних воздействий, либо покоится, либо движется равномерно и прямолинейно.
Первый закон Ньютона:

Масса тела — физическая величина, являющаяся одной из основных характеристик материи, определяющая ее инерционные и гравитационные свойства.
Мера инертности тела – это его масса.
Сила — это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры.
Второй закон Ньютона
Второй закон Ньютона — основной закон динамики поступательного движения:
«Ускорение, с которым движется тело, прямопропорционально силе, действующей на тело, и обратнопропорционально массе тела».

Импульсом материальной точки (количеством движения) называется векторная величина численно равная произведению массы материальной точки на ее скорость и имеющая направление скорости.
скорость изме­нения импульса материальной точки равна действующей на нее силе.
Тогда общая формулировка второго закона Ньютона:

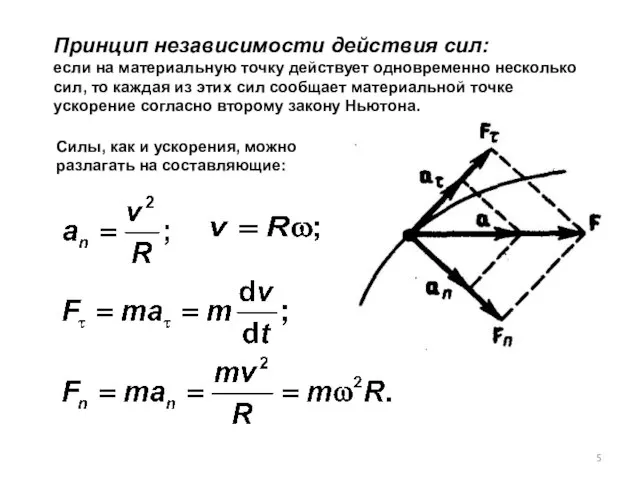
Принцип независимости действия сил:
если на материальную точку действует одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение согласно второму закону Ньютона.
Силы, как и ускорения, можно разлагать на составляющие:

Третий закон Ньютона:
«Силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки».

2.2. Закон сохранения импульса
Замкнутой (изолированной) называется такая механическая система тел, на которую не действуют внешние силы.
«Импульс в замкнутой системе не изменяется с течением времени».
Закон сохранения импульса является следствием однородности пространства:
при параллельном переносе в пространстве замкнутой системы тел как целого ее физические свойства не изменяются.

В механике Галилея—Ньютона масса не зависит от скорости. Импульс системы может быть выражен через скорость ее центра масс.
Центром масс (или центром инерции) системы материальных точек называется воображаемая точка С, положение которой характеризует распределение массы этой системы.
— ра­диус-вектор системы,
где mi и ri — соответственно масса и радиус-вектор i-й материальной точки;
n — число материальных точек в системе.
— масса системы.
2.3. Закон движения центра масс.

Скорость центра масс:
Учитывая, что pi = mivi , a
есть импульс р системы, то можно
Импульс системы равен произведению массы системы на скорость ее центра масс.
записать:

т. е. центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, приложенных к системе.
Закон движения центра масс:
«центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается непо­движным».

2.4. Силы в механике
1. Сила тяжести или гравитационная сила – это сила, с которой тело притягивается к земле.
В системе отсчета, связанной с землей, на всякое тело массой m действует сила:
Все тела падают на землю с одинаковым ускорением, которое называется ускорением свободного падения:
Весом тела называется сила, с которой тело вследствие тяготения к земле действует на опору или натягивает нить подвеса.

Сила тяжести действует всегда, а вес тела проявляется лишь тогда, когда на тело действуют другие силы.
Сила тяжести равна весу тела лишь тогда, когда ускорение тела относительно Земли равно нулю.
где a – ускорение тела с опорой относительно Земли.
В противном случае:
Если тело движется в поле тяготения, то:
и вес будет равен нулю, т.е. тело будет невесомым.
Невесомость – это состояние тела, при котором оно движется только под действием силы тяжести.

2. Сила упругости возникает в результате взаимодействия тел, сопровождающегося их деформацией.
Сила упругости пропорциональна смещению тела относительно положения равновесия и направлена к положению равновесия.
Пример такой силы – сила упругости пружины:

3. Сила трения – это сила, которая препятствует скольжению соприкасающихся тел друг относительно друга.
Трение разделяют на: трение скольжения, качения и верчения.
Внутренним трением называется трение между частями одного и того же тела, например между различными слоями жидкости или газа, скорости которых меняются от слоя к слою.
Различают внешнее (сухое) и внутреннее (жидкое или вязкое) трение.
Внешним трением называется трение, возникающее в плоскости касания двух соприкасающихся тел при их относительном перемещении.

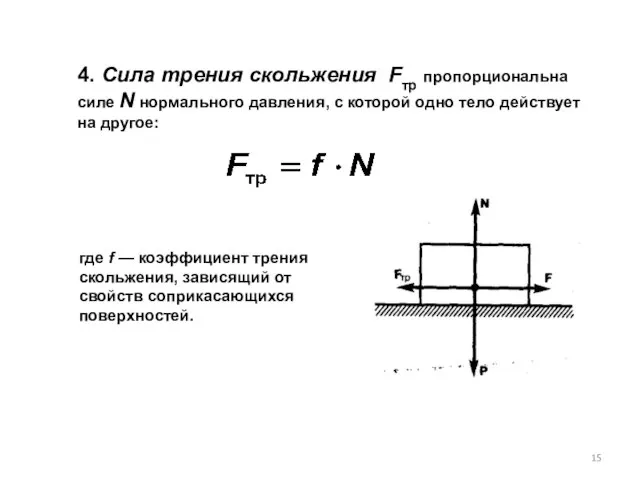
4. Cила трения скольжения Fтр пропорциональна силе N нормального давления, с которой одно тело действует на другое:
где f — коэффициент трения скольжения, зависящий от свойств соприкасающихся поверхностей.

Тело находится на наклонной плоскости с углом наклона α .
Тело приходит в движение, когда тангенциальная составляющая F силы тяжести Р больше силы трения Fтр.
Сила трения качения определяется по закону, установленному Кулоном:
r — радиус катящегося тела; fк — коэффициент трения качения.

3. Работа и энергия
Энергия — универсальная мера различных форм движения и взаимодействия.
Энергия бывает: механическая, тепловая, электромагнитная, ядерная и др.
Работа силы – количественная характеристика процесса обмена энергией между взаимодействующими телами.
Если тело движется прямолинейно и на него действует постоянная сила F, которая составляет некоторый угол a с направлением перемещения, то работа этой силы:
3.1. Энергия, работа, мощность

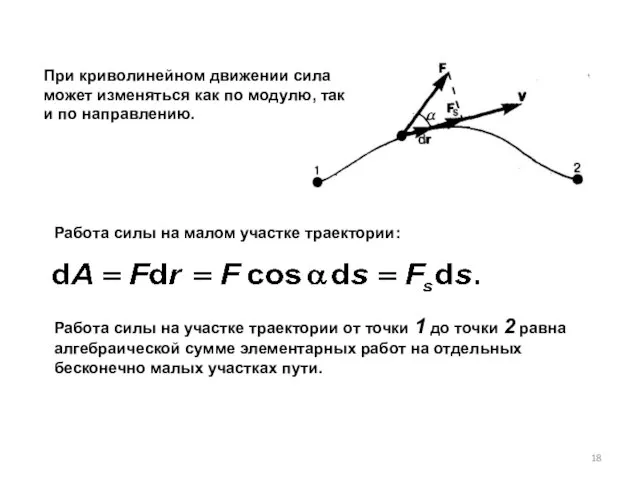
При криволинейном движении сила может изменяться как по модулю, так и по направлению.
Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути.
Работа силы на малом участке траектории:

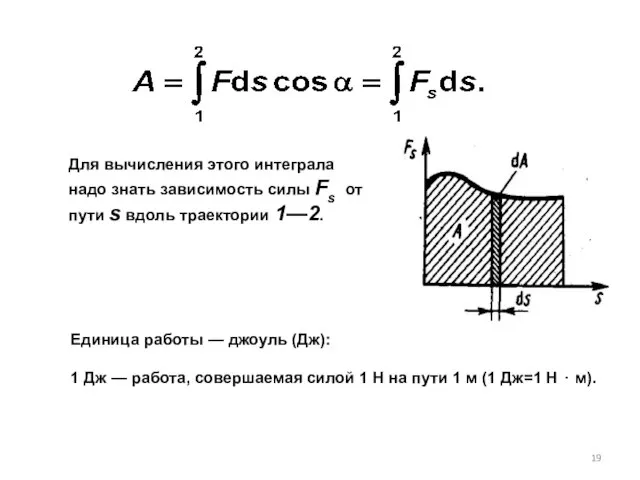
Для вычисления этого интеграла надо знать зависимость силы Fs от пути s вдоль траектории 1—2.
Единица работы — джоуль (Дж):
1 Дж — работа, совершаемая силой 1 Н на пути 1 м (1 Дж=1 Н ⋅ м).

За время dt сила F совершает работу Fdr,
а мощность, развиваемая этой силой, в данный момент времени:
т. е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы;
N — величина скалярная.
Единица мощности — ватт (Вт):
1 Вт — мощность, при которой за время 1 с совершается работа 1 Дж (1 Вт = 1 Дж/с).
Мощность – это скорость совершения работы::

Кинетическая энергия механической системы — это энергия механического движения этой системы.
3.2. Кинетическая и потенциальная энергии
Приращение кинетической энергии на элементарном перемещении равно элементарной работе на этом перемещении:

Потенциальная энергия — механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.
Потенциальная энергия есть функция состояния системы. Она зависит только от конфигурации системы и от ее положения по отношению к внешним телам.
Примеры потенциальной энергии.
1. Потенциальная энергия тела массой m, поднятого над землей на высоту h:
2. Потенциальная энергия пружины, растянутой на длину x :

«в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется».
Закон сохранение механической энергии:
Консервативной называется сила, работа которой не зависит от траектории перемещения тела из одной точки в другую.
Полная механическая энергия механической системы:

Механические системы, на тела которых действуют только консервативные силы (внутренние и внешние), называются консервативными системами.
Закон сохранения механической энергии можно сформулировать еще так:
«в консервативных системах полная механическая энергия сохраняется».
Диссипативные системы – это такие, в которых механическая энергия постепенно уменьшается за счет преобразования в другие формы энергии.
Процесс уменьшения механической энергии за счет преобразования в другие формы энергии получил название диссипации (или рассеяния) энергии.