Презентация на тему Динамика Сила тяжести и вес работа энергии

Сила тяжести и вес с точки зрения теории тяготения
Если пренебречь суточным вращением Земли вокруг своей оси, то сила тяжести Р и сила гравитационного тяготения F равны между собой:
где М  масса Земли, R  расстояние между телом и центром Земли, G  гравитационная постоянная.
Пусть тело находится на высоте h от поверхности Земли, тогда
т. е. сила тяжести Р(h) с удалением от поверхности Земли уменьшается. Из последних соотношений получаем зависимость ускорения свободного падения от высоты h от поверхности Земли:
где gо – ускорение свободного падения
у поверхности Земли.

В физике применяется также понятие веса тела.
Весом тела называют силу, с которой тело действует на опору (или подвес), удерживающую тело от свободного падения. То есть вес тела действует не на само тело, а на другое тело, удерживающее его.
Таким образом, сила тяжести действует всегда, а вес тела проявляется только в том случае, когда на тело кроме силы тяжести действуют еще другие силы. Например, тела, находящиеся в космических кораблях, свободно движущихся в космосе, являются невесомыми, их вес равен нулю.
Сила тяжести равна весу только тогда, когда ускорение тела относительно Земли равно нулю.

Работа в поле тяготения. Потенциал поля тяготения
Рассмотрим, чему равна работа, совершаемая силами поля тяготения при перемещении в нем материальной точки массой т.
Вычислим, например, какую надо затратить работу для удаления тела массой т от Земли. На расстоянии R на данное тело действует сила тяготения Ньютона и при перемещении этого тела на расстояние dR затрачивается работа
Знак минус появляется потому, что сила и перемещение в данном случае противоположны по направлению .
Если тело перемещать с расстояния R1 до R2, то затрачивается работа

Из последней формулы вытекает, что затраченная работа в поле тяготения не зависит от траектории перемещения, а определяется лишь начальным и конечным положениями тела, т. е. поле тяготения является потенциальным , а силы тяготения называются консервативными.
Работа, совершаемая консервативными силами, равна изменению потенциальной энергии системы, взятому со знаком минус, т. е.
Так как в формулы входит только разность потенциальных энергий в двух состояниях, то для удобства принимают потенциальную энергию при R2→∞ равной нулю (P2=0). Тогда потенциальная энергия поля тяготения запишется в виде
а величина
называется потенциалом поля тяготения.

Первая космическая скорость
Пе́рвая косми́ческая ско́рость (кругова́я ско́рость) — скорость, которую необходимо придать объекту, который после этого не будет использовать реактивное движение, чтобы вывести его на круговую орбиту (пренебрегая сопротивлением атмосферы и вращением планеты). Иными словами, первая космическая скорость — это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите.
Пе́рвая косми́ческая ско́рость
вычисляется из равенства силы тяжести
центростремительной силе:
Или, учитывая, что g = GM/R²,

Вторая космическая скорость
Втора́я косми́ческая ско́рость (параболи́ческая ско́рость, ско́рость освобожде́ния, ско́рость убега́ния) — наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), для преодоления гравитационного притяжения небесного тела.
Параболической вторая космическая скорость называется потому, что тела, имеющие при старте скорость, в точности равную второй космической, движутся по дуге параболы относительно небесного тела. Однако, если энергии телу придано чуть больше, его траектория перестает быть параболой и становится гиперболой; если чуть меньше, то она превращается в эллипс.
Для получения формулы второй космической скорости удобно обратить задачу — спросить, какую скорость получит тело на поверхности планеты, если будет падать на неё из бесконечности. Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния.
Запишем закон сохранения энергии

Решая это уравнение относительно v2 , получим
Между первой и второй космическими скоростями существует простое соотношение:
Вообще, космическая скорость -это минимальная скорость, при которой какое-либо тело в свободном движении с поверхности небесного тела сможет:
v1 (круговая скорость) — стать спутником небесного тела (то есть вращаться по круговой орбите на нулевой или пренебрежимо малой высоте относительно поверхности);
v2 (параболическая скорость, скорость убегания) — преодолеть гравитационное притяжение небесного тела и уйти в бесконечность;
v3 — покинуть звёздную систему, преодолев притяжение звезды;
v4 — покинуть галактику.

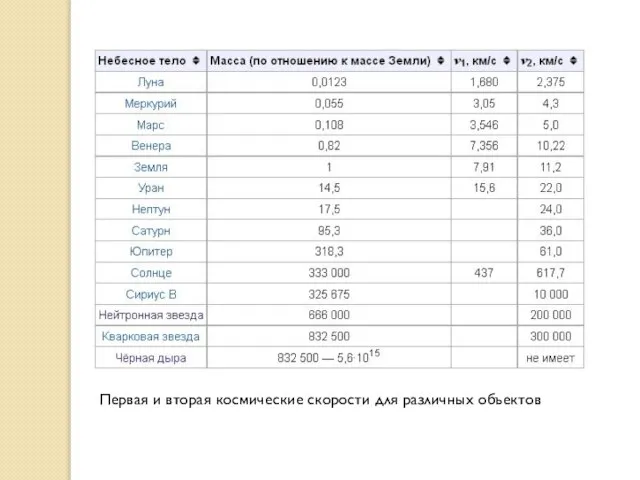
Первая и вторая космические скорости для различных объектов

Задание 1
Космический корабль улетает от Земли. Как направлен вектор ускорения корабля в тот момент, когда вектор силы гравитационного притяжения Земли направлен под углом к вектору скорости корабля? Действие остальных тел на корабль пренебрежимо мало.
Решение
Согласно второму закону Ньютона, ускорение тела сонаправлено с равнодействующей всех сил. Поскольку действием остальных тел на корабль можно пренебречь, на него действует только сила гравитационного притяжения со стороны Земли. Таким образом, вектор ускорения корабля направлен по направлению вектора силы.

Задание 2
У поверхности Земли на космонавта действует сила тяготения 720 Н. Какая сила тяготения действует со стороны Земли на того же космонавта в космическом корабле, движущемся по круговой орбите вокруг Земли на расстоянии трех земных радиусов от ее центра?
Решение
По закону всемирного тяготения сила притяжения космонавта со стороны Земли обратно пропорциональна квадрату расстояния между ним и центром Земли.
У поверхности Земли это расстояние совпадает
с радиусом планеты. На космическом корабле,
по условию, оно в три раза больше . Таким образом,
сила тяготения со стороны Земли, действующая на
космонавта на космическом корабле,
в 9 раз меньше, чем у поверхности Земли,
то есть

Задание 3
Космонавт на Земле притягивается к ней с силой 700 Н. С какой приблизительно силой он будет притягиваться к Марсу, находясь на его поверхности, если радиус Марса в 2 раза, а масса — в 10 раз меньше, чем у Земли?
Решение

Задание 4
Какова минимальная скорость падения метеорита на Луну?
Решение
Как следует из закона сохранения энергии, какую бы скорость ни имело тело на границе сферы действия Луны, при касании лунной поверхности она не может быть меньше скорости убегания с поверхности Луны, 2.4 км/с.

Задание 5
Искусственный спутник Земли движется по круговой орбите.
Чему равно отношение его гравитационной потенциальной энергии к
кинетической энергии?
Решение
Потенциальная гравитационная энергия спутника по модулю равна
Так как
то кинетическая энергия спутника равна
Отсюда

Физика падения бутерброда
Распространено убеждение, что бутерброд практически всегда падает намазанной частью вниз (закон бутерброда или закон подлости). Оно не лишено оснований.
«И так уйдут за годом год, так и жизнь пройдет,
И в сотый раз маслом вниз упадет бутерброд…»
В.Цой
В 1996 году физик Роберт Мэттьюз из университета Эстона (Англия) получил Шнобелевскую премию за работу «Падающий бутерброд, закон Мэрфи и мировые постоянные», посвящённую тщательному исследованию закона Мерфи и особенно проверке его следствия: бутерброд чаще падает на землю маслом вниз. Мэттьюз вывел формулу для обоснования своих доводов.
Физики шутят…

Парадо́кс ко́шки с ма́слом - парадокс, основанный на двух народных мудростях:
кошки всегда приземляются на лапы;
бутерброд всегда падает маслом вниз (закон бутерброда или закон подлости).
Противоречие возникает, если рассмотреть кошку, к спине которой прикреплён бутерброд (маслом вверх), падающую на пол.
Некоторые исследователи утверждают, что результатом эксперимента станет антигравитация. По их словам, падение кошки замедлится с приближением к земле, а она начнёт вращаться, пытаясь приземлиться на лапы, но в то же время и на масло бутерброда. В конце концов, она должна достигнуть стабильного состояния, вися недалеко от земли и вращаясь с большой скоростью. Однако, по утверждениям других, вращение можно стабилизировать.

Законы сохранения
Любое тело (или совокупность тел) представляет собой, по существу, систему материальных точек или частиц. Если система с течением времени изменяется, то говорят, что изменяется ее состояние. Состояние системы характеризуется одновременным заданием положений (координат) и скоростей всех ее частиц.
Зная законы действующих на частицы системы сил и состояние системы в некоторый начальный момент времени, можно, как показывает опыт, с помощью уравнений движения предсказать ее дальнейшее поведение, т.е. найти состояние системы в любой момент времени. Так, например, решается задача о движении планет Солнечной системы.
Однако детальное рассмотрение поведения системы с помощью уравнений движения часто бывает настолько затруднительно (например, из-за сложности самой системы), что довести решение до конца представляется практически невозможным. А в тех случаях, когда законы действующих сил вообще неизвестны, такой подход оказывается в принципе неосуществимым. Кроме того, существует ряд задач, в которых детальное рассмотрение движения отдельных частиц просто и не имеет смысла (например, описание движения отдельных молекул газа).

В связи с этим возникает вопрос: нет ли каких-либо общих принципов, являющихся следствием законов Ньютона, которые позволяют упростить решение многих практических задач?
Оказывается, такие принципы есть. Это законы сохранения.
Как уже было сказано, при движении системы ее состояние изменяется со временем. Однако существуют такие величины, характеризующие состояние системы, которые обладают весьма важным и замечательным свойством сохраняться во времени. Среди этих сохраняющихся величин наиболее важную роль играют энергия, импульс и момент импульса.
Эти три величины обладают важным свойством – аддитивностью: их значение для системы, состоящей из частей, равно сумме значений каждой из частей в отдельности. Энергия обладает этим свойством в случае отсутствия заметного взаимодействия между частями системы, а импульс и момент импульса – и при наличии взаимодействия. Свойство аддитивности и придает этим трем величинам особую роль.

Законы сохранения энергии, импульса и момента импульса связаны с фундаментальными свойствами времени и пространства.
Закон сохранения энергии связан с однородностью времени, а законы сохранения импульса и момента импульса  соответственно с однородностью и изотропностью пространства.
Однородность времени означает, что все моменты времени эквивалентны и физические законы не изменяются со временем, т.е. не зависят от начала отсчета времени.
Однородность пространства заключается в том, что при параллельном переносе в пространстве замкнутой системы тел как целого её физические законы и законы движения не изменяются (не зависят от выбора положения начала координат инерциальной системы отсчета).
Изотропность пространства означает одинаковость свойств пространства по всем направлениям, т.е. независимость физических законов от выбора направления координат системы отсчета.

Энергия, работа, мощность
Энергия  универсальная мера различных форм движения и взаимодействия. С различными формами движения материи связывают различные формы энергии: механическую, тепловую, электромагнитную, ядерную и др. В одних явлениях форма движения материи не изменяется (например, горячее тело нагревает холодное), в других  переходит в иную форму (например, в результате трения механическое движение превращается в тепловое).
Однако во всех случаях энергия, отданная (в той или иной форме) одним телом другому телу, равна энергии, полученной вторым телом.
Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы. Работа является мерой изменения энергии.

Если тело движется прямолинейно и на него действует постоянная сила , которая составляет некоторый угол  с направлением перемещения , то элементарная работа dA этой силы равна скалярному произведению этих векторов, т.е. произведению проекции силы Fs на направление перемещения (Fs=Fcos), умноженной на перемещение точки приложения силы

Если вектор силы и направление перемещения образуют острый угол (cos0), работа положительна.
Если угол  - тупой (cos0), работа отрицательна.
При =/2 работа равна нулю.
Последнее обстоятельство особенно отчетливо показывает, что понятие работы в механике существенно отличается от обыденного представления о работе. В обыденном понимании всякое усилие, в частности мускульное напряжение, всегда сопровождается совершением работы. Например, для того чтобы держать тяжелый груз, стоя неподвижно или перемещать его горизонтально, носильщик затрачивает много усилий, т.е. «совершает работу». Однако работа как механическая величина в этих случаях равна нулю, а энергия груза при этом не изменяется.

Если при перемещении точки приложения сила изменяется как по величине, так и по направлению, то нужно вычислить элементарную работу dA на каждом бесконечно малом участке пути dS, равную FsdS, а затем сложить значения всех элементарных работ вдоль всего участка пути.

Эта сумма приводится к интегралу
который называется криволинейным интегралом вдоль траектории 12 (часто кривую 12 обозначают одной буквой L).
Единица работы  джоуль (Дж): 1 Дж  работа, совершаемая силой в 1 Н при перемещении на 1 м при условии, что направление силы совпадает с направлением перемещения. (1 Дж = 1 Нм).
Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности. Мощность – это работа, совершаемая силой за единицу времени. Если за время dt совершается работа dA, то мощность равна

За время dt сила совершает работу и мощность, развиваемая этой силой, в данный момент времени
т. е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы; Р  величина скалярная.
Зная мощность силы , можно найти и работу, которую совершает эта сила за промежуток времени t:
Единица мощности  ватт (Вт):
1 Вт  мощность, при которой за 1 с
совершается работа в 1 Дж (1 Вт = 1 Дж/с).
Внесистемная единица измерения
мощности -лошадиная сила (л.с.),
1 л.с. = 735 Вт.

Кинетическая энергия
Пусть частица массы m движется под действием некоторой силы. Найдем элементарную работу, которую совершает эта сила на элементарном перемещении. Учитывая, что
получим
Отсюда видно, что работа результирующей силы идет на приращение некоторой величины (стоящей в скобках), которую называют кинетической энергией:
Таким образом, приращение кинетической энергии частицы при элементарном перемещении равно
а при конечном перемещении из точки 1 в точку 2
т.е. приращение кинетической энергии частицы при некотором перемещении равно алгебраической сумме работ всех действующих сил.

Полученный результат без труда обобщается на случай произвольной системы материальных точек.
Кинетической энергией системы называется сумма кинетических энергий материальных точек, из которых эта система состоит или на которые ее можно мысленно разделить.
Таким образом, работа всех сил, действующих на систему материальных точек, равна приращению кинетической энергии системы.
Кинетическая энергия зависит только от массы и скорости тела, т. е. кинетическая энергия системы есть функция состояния ее движения.
При выводе формул предполагалось, что движение рассматривается в инерциальной системе отсчета. В разных инерциальных системах отсчета, движущихся друг относительно друга, скорость тела, а, следовательно, и его кинетическая энергия будут неодинаковы. Таким образом, кинетическая энергия зависит от выбора системы отсчета.

Потенциальная энергия
Потенциальная энергия  это энергия, определяемая взаимным расположением тел и характером сил взаимодействия между ними.
Пусть, F(x, y, z)  сила, действующая на тело. Тогда элементарная работа этой силы по перемещению тела равна
Введем функцию U(x, y, z), удовлетворяющую следующим условиям:
Функцию U(x, y, z), удовлетворяющую данным условиям , называют потенциальной функцией, а силу – консервативной (или потенциальной) силой. При этом элементарная работа dA будет равна:

Пусть тело под действием силы перемещается из точки 1 в точку 2, тогда работа этой силы при таком перемещении равна
где U1 и U2 начальные и конечные значения потенциальной функции U(x, y, z). Работа консервативной силы на любом замкнутом пути равна нулю, так как в этом случае U1=U2.
Таким образом, работа консервативной силы зависит лишь от начального и конечного положения точек пути, и не зависит от пути, пройденного телом.
Если, например, тело переходит под действием силы тяжести с высоты h0 над уровнем Земли на высоту h, то работа зависит не от того, по какому пути тело двигалось, а лишь от начального и конечного уровней.
Потенциальная функция U, определяемая соотношениями, связывающими её с консервативной силой, называется потенциальной энергией.
Если же работа, совершаемая силой, зависит от пути, то такая сила называется диссипативной (например, сила трения).

Итак, тело, находясь в поле консервативных сил, называемом потенциальным полем, обладает потенциальной энергией U(x, y, z).
Работа консервативных сил при любом элементарном изменении конфигурации системы равна приращению её потенциальной энергии, взятому со знаком минус, так как работа совершается за счет убыли потенциальной энергии dA= dU.
Поскольку начало отсчета (состояние с энергией U1) выбирается произвольно, то потенциальная энергия U системы может иметь отрицательное значение.
Если принять за нуль потенциальную энергию тела, лежащего на поверхности Земли, то потенциальная энергия тела, находящегося на дне шахты глубиной h, равна U = mgh.
Таким образом, потенциальная энергия системы определяется с точностью до постоянной величины и в зависимости от начала отсчета может принимать положительные или отрицательные значения. В то же время её кинетическая энергия независимо от системы отсчета может принимать только положительные значения.

Пример 1.
Рассмотрим растяжение (сжатие) пружины. Согласно закону Гука сила упругости пропорциональна удлинению пружины х, взятому с обратным знаком, т.е. F = kx, где k  жесткость (коэффициент упругости) пружины. С другой стороны согласно F = dU/dx.
Из приведенных двух выражений заключаем, что потенциальная энергия упругой деформации U равна
То есть ружина (упругое тело) приобретает энергию за счет работы А внешней силы. Эта работа является мерой изменения потенциальной энергии деформируемого тела (пружины), т.е. А = U.

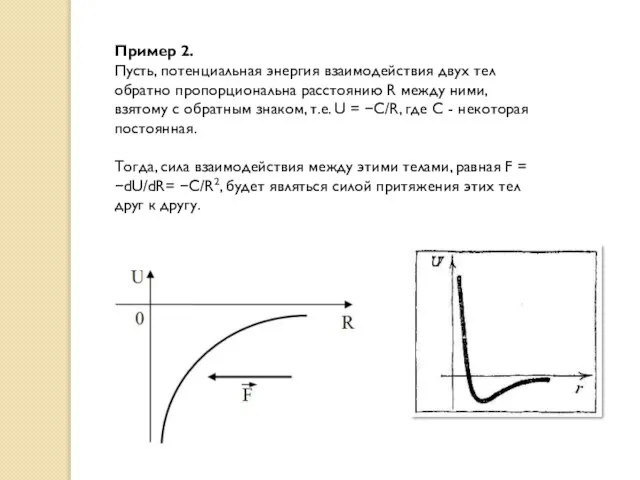
Пример 2.
Пусть, потенциальная энергия взаимодействия двух тел обратно пропорциональна расстоянию R между ними, взятому с обратным знаком, т.е. U = С/R, где С - некоторая постоянная.
Тогда, сила взаимодействия между этими телами, равная F = dU/dR= С/R2, будет являться силой притяжения этих тел друг к другу.

Закон сохранения энергии
Закон сохранения энергии  результат обобщения многих экспериментальных данных. Идея этого закона принадлежит М.В.Ломоносову (17111765), изложившему закон сохранения материи и движения, а количественная формулировка закона сохранения энергии дана немецким врачом Ю. Майером (18141878) и немецким естествоиспытателем Г. Гельмгольцем (18211894).

Полная механическая энергия системы  энергия механического движения и взаимодействия равна сумме кинетической и потенциальной энергий E=T+U.
Пусть на рассматриваемое тело действуют только потенциальные силы.
Для такого случая работа против этих сил dA =  dU.
В свою очередь приращение кинетической энергии происходит за счет работы этих сил, т.е. dT = dA.
Отсюда находим, что
dT =  dU , d(T + U) = dE = О, E = T + U = const.
Таким образом, выполняется закон сохранения полной механической энергии, равной сумме кинетической и потенциальной энергий, если на тело действуют только потенциальные(консервативные) силы.
Закон неразумного сохранения грязи:
Чтобы одно очистить, нужно другое запачкать.

Системы, в которых действуют диссипативные силы, например силы трения, называются диссипативными.
В диссипативных системах полная механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы энергии, например, во внутреннюю энергию (внутренняя энергия складывается из кинетической энергии невидимого беспорядочного движения атомов и молекул вещества и потенциальной энергии их взаимодействия). Этот процесс получил название диссипации (или рассеяния) энергии.
Строго говоря, все реальные макроскопические системы в природе являются диссипативными.
Следовательно, в реальных случаях закон сохранения механической энергии не выполняется. Однако при «исчезновении» механической энергии всегда возникает эквивалентное количество энергии другого вида. Таким образом, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой. В этом и заключается физическая сущность закона сохранения и превращения энергии.

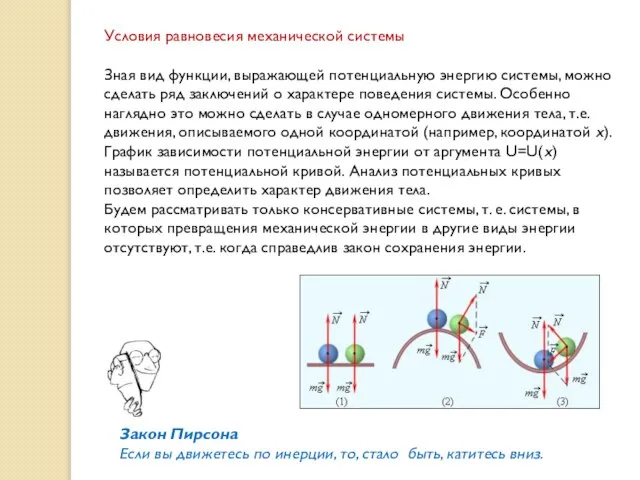
Условия равновесия механической системы
Зная вид функции, выражающей потенциальную энергию системы, можно сделать ряд заключений о характере поведения системы. Особенно наглядно это можно сделать в случае одномерного движения тела, т.е. движения, описываемого одной координатой (например, координатой х). График зависимости потенциальной энергии от аргумента U=U(x) называется потенциальной кривой. Анализ потенциальных кривых позволяет определить характер движения тела.
Будем рассматривать только консервативные системы, т. е. системы, в которых превращения механической энергии в другие виды энергии отсутствуют, т.е. когда справедлив закон сохранения энергии.
Закон Пирсона
Если вы движетесь по инерции, то, стало быть, катитесь вниз.

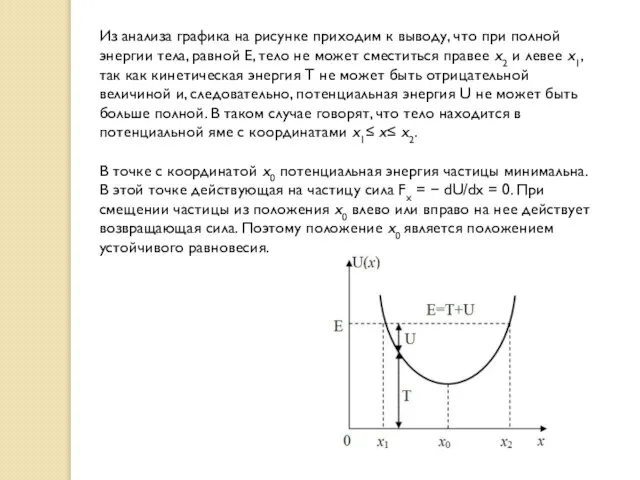
Из анализа графика на рисунке приходим к выводу, что при полной энергии тела, равной Е, тело не может сместиться правее х2 и левее х1, так как кинетическая энергия Т не может быть отрицательной величиной и, следовательно, потенциальная энергия U не может быть больше полной. В таком случае говорят, что тело находится в потенциальной яме с координатами х1 х х2.
В точке с координатой х0 потенциальная энергия частицы минимальна. В этой точке действующая на частицу сила Fx =  dU/dx = 0. При смещении частицы из положения х0 влево или вправо на нее действует возвращающая сила. Поэтому положение х0 является положением устойчивого равновесия.

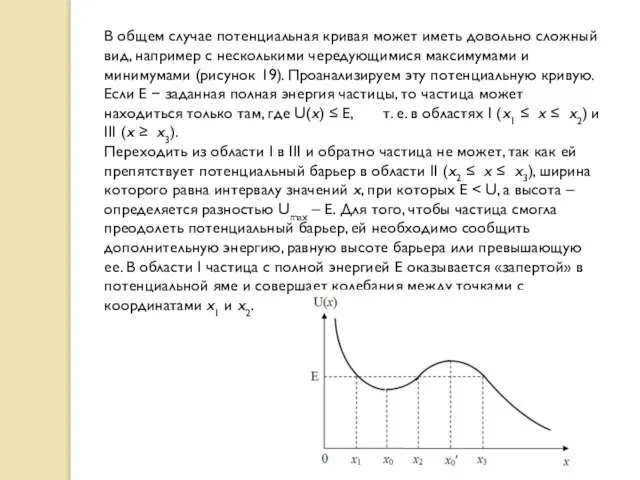
В общем случае потенциальная кривая может иметь довольно сложный вид, например с несколькими чередующимися максимумами и минимумами (рисунок 19). Проанализируем эту потенциальную кривую. Если Е  заданная полная энергия частицы, то частица может находиться только там, где U(x)  E, т. е. в областях I (х1  х  х2) и III (х  х3).
Переходить из области I в III и обратно частица не может, так как ей препятствует потенциальный барьер в области II (х2  х  х3), ширина которого равна интервалу значений х, при которых Е < U, а высота – определяется разностью Umax – Е. Для того, чтобы частица смогла преодолеть потенциальный барьер, ей необходимо сообщить дополнительную энергию, равную высоте барьера или превышающую ее. В области I частица с полной энергией Е оказывается «запертой» в потенциальной яме и совершает колебания между точками с координатами x1 и x2.

В точке с координатой x0 потенциальная энергия частицы минимальна.
Так как действующая на частицу сила Fx =  dU/dx, а условие минимума потенциальной энергии dU/dx = 0, то в точке с координатой x0 сила Fx(x0) = 0. При смещении частицы из положения x0 (и влево, и вправо) она испытывает действие возвращающей силы, поэтому положение x0 является положением устойчивого равновесия.
Указанные условия выполняются и для точки x0 (для Umax). Однако эта точка соответствует положению неустойчивого равновесия, так как при смещении частицы из положения x0 появляется сила, стремящаяся отклонить ее от этого положения.

Индийская мудрость
Чувство юмора - это способность смеяться над собой. Часто юмор полезнее, чем лекции.