Содержание
- 2. КВАДРАТ СУММЫ И КВАДРАТ РАЗНОСТИ
- 3. КВАДРАТ СУММЫ При умножении многочлена на многочлен каждый член одного многочлена умножают на каждый член другого.
- 4. Формулировка формулы квадрата суммы: Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого
- 5. Пример №1 Представьте в виде многочлена: a) (x + 2y)2 = x2 + 2 ·x·2y
- 6. КВАДРАТ РАЗНОСТИ (a b)2 (a b)(a b) a2 ab
- 7. Формулировка формулы квадрата разности: Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого
- 8. Пример №2 Представьте в виде многочлена: а) (2a – c)2 = (2a)2-2·2a·c + c2 =
- 9. Запомни! (а+b)²= а²+2аb+b² (а-b)² = а²-2аb+b²
- 10. Разложение на множители с помощью формул квадрата суммы и квадрата разности a2 2ab b2
- 11. Пример №3 Представьте многочлен в виде квадрата двучлена:
- 12. Решение задач на применение формул квадрата суммы и квадрата разности
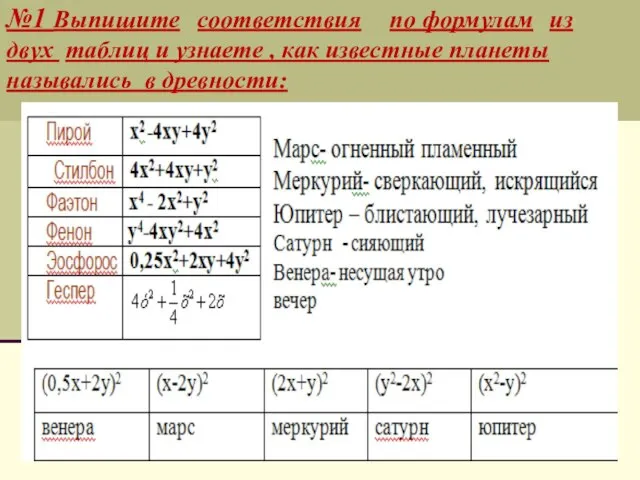
- 13. №1 Выпишите соответствия по формулам из двух таблиц и узнаете , как известные планеты назывались в
- 14. Решение 1) Пирой - Марс ; 2) Стилбон - Меркурий; 3) Фаэтон - Юпитер; 4) Фенон
- 15. №1 Найдите ошибку: 1)(3а – 2в)² = 9а² + 12 ва + 4в²; 2) (2у +
- 16. Решение 1)(3а – 2в)² = 9а² + 12 ва + 4в²; (3а – 2в)² = 9а²
- 17. Задачи для самостоятельной работы
- 18. Выполните тестовое задание
- 19. Выберите правильный вариант ответа в № 1 - 3
- 20. №1 ВЫБЕРИТЕ СООТВЕТСТВИЯ ПО ФОРМУЛАМ ( НАПРИМЕР, 1 – ВЕНЕРА): 1.(х+ а)²= 2.(а- 2х)² = 3.(х
- 21. №2 Найдите ошибку в каждом из равенств и запишите правильное решение: 1) (в - у)² =
- 22. №3 ВСТАВЬТЕ ПРОПУЩЕННЫЕ ЗНАКИ В ВЫРАЖЕНИЯХ И ЗАПИШИТЕ ВЕРНОЕ РАВЕНСТВО: а) (х...у)2=х2 -2х+... б) (...-...)2=9х2... ...+25у2
- 24. Скачать презентацию




















 Переливание крови
Переливание крови Вербальные и невербальные средства общения
Вербальные и невербальные средства общения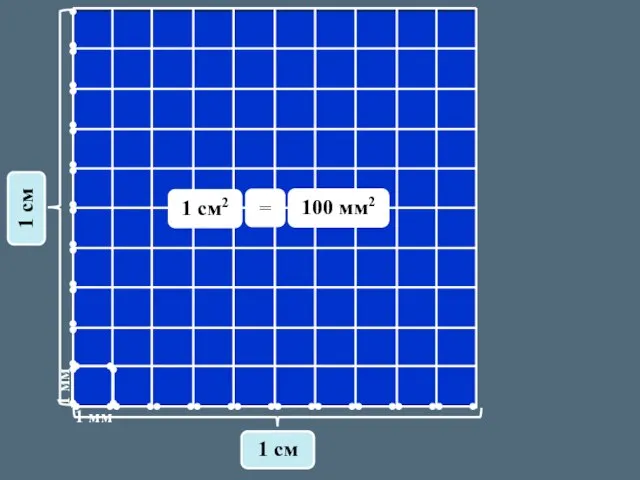 1 мм2
1 мм2 Feelings and emotions
Feelings and emotions Во все века героизм и мужество воинов России, мощь и слава русского оружия были неотъемлемой частью величия Российского государст
Во все века героизм и мужество воинов России, мощь и слава русского оружия были неотъемлемой частью величия Российского государст ЗАО “Актив Успеха” внедряет на предприятии систему менеджмента качества в соответствии со стандартом ISO 9001 (ГОСТ Р ИСО 9001-2001).
ЗАО “Актив Успеха” внедряет на предприятии систему менеджмента качества в соответствии со стандартом ISO 9001 (ГОСТ Р ИСО 9001-2001). Способы воздействия в межличностной коммуникации
Способы воздействия в межличностной коммуникации Псалом 19. Святорусский текст церковнославянской псалтири
Псалом 19. Святорусский текст церковнославянской псалтири Мир художественной культуры
Мир художественной культуры Зарубежная Европа. Обострение межнациональных отношений
Зарубежная Европа. Обострение межнациональных отношений Техника продаж для КП, направления II
Техника продаж для КП, направления II Изменения в культуре и быте в первой четверти 18 века
Изменения в культуре и быте в первой четверти 18 века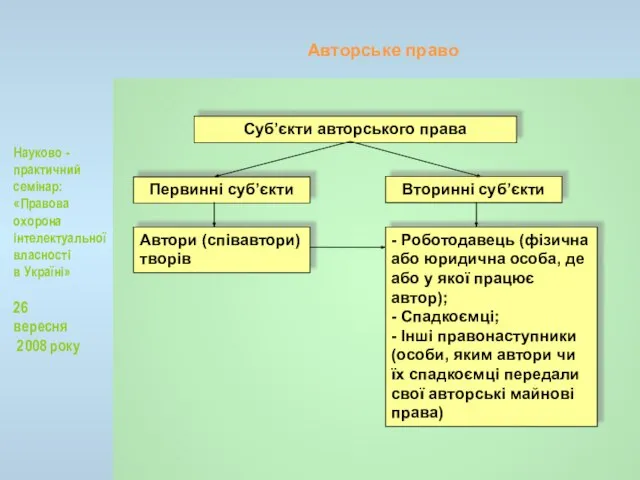 Авторское право
Авторское право Ирландские иллюминированные Евангелия
Ирландские иллюминированные Евангелия Перечень документации, которая должна быть в каждой организации
Перечень документации, которая должна быть в каждой организации Принцип работы NOTAR
Принцип работы NOTAR School of our dreams
School of our dreams Молодежные гранты и стипендии
Молодежные гранты и стипендии  Механизмы психологической защиты и совладания
Механизмы психологической защиты и совладания Music
Music THE GREAT GATSBY 1896 — 1940
THE GREAT GATSBY 1896 — 1940 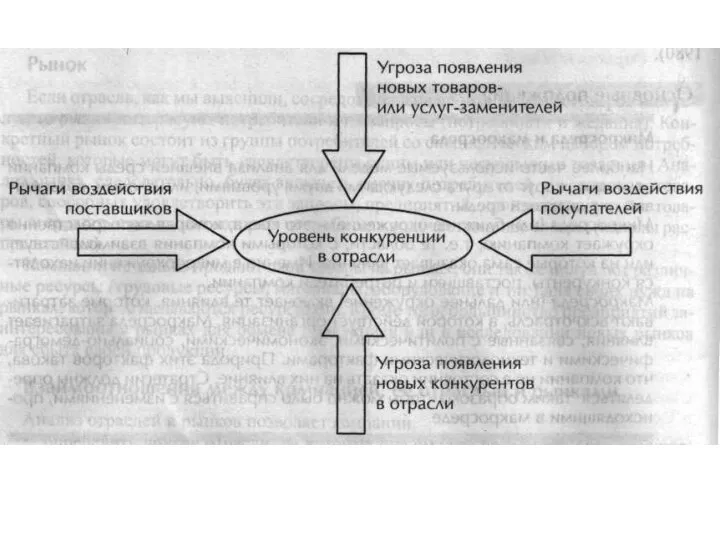 Уровень конкуренции в отрасли
Уровень конкуренции в отрасли Князь Владимир на картинах художников
Князь Владимир на картинах художников Проект постановленияПравительства Омской области «О величине прожиточного минимума на душу населения и по основным социально-
Проект постановленияПравительства Омской области «О величине прожиточного минимума на душу населения и по основным социально- Космос – история и будущее
Космос – история и будущее Использование здоровье сберегающих технологий педагогами в педагогическом процессе ДОУ
Использование здоровье сберегающих технологий педагогами в педагогическом процессе ДОУ Гидравлическая очистка вагонов водой. Модернизация установки
Гидравлическая очистка вагонов водой. Модернизация установки Form and content
Form and content