Презентация на тему Функции распределения случайной величины плотность распределения

Функция распределения вероятностей случайной величины Х называется числовая функция F(x), определяющая вероятность того, что случайная величина Х примет значение, меньше х:
F(x)=P(X
где любое х- любое действительное число.
Иногда функцию распределения F(x) называют интегральной функцией распределения.
Функция распределения случайной величины

Свойства функции распределения
Значения функции распределения F(x) принадлежат отрезку [0;1]:
0≤ F(x) ≤ 1
Функции распределения F(x) есть неубывающая функция, т.е.
F(x2) ≥F(x1) , если х2>x1
Вероятность того, что случайная величина Х примет значение, заключенное в интервале (а,b), равна приращению интегральной функции на этом интервале: Р(а<Х
Если все возможные значения случайной величины Х принадлежат интервалу (а,b), то F(х)=0 при х≤ а; F(x)=1 при х ≥ b
Для функции распределения справедливы следующие предельные соотношения:
Lim F(x)=0 Lim F(x)=0
x ∞
x ∞

Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Она полностью характеризует случайную величину и является одной из форм закона распределения.
Для дискретной случайной величины функция распределения имеет вид:
Знак неравенства под знаком суммы показывает, что суммирование распространяется на те возможные значения случайной величины, которые меньше аргумента х.
Функция распределения дискретной случайной величины Х разрывна и возрастает скачками при переходе через каждое значение хi

Пример:

Функция распределения полностью характеризует случайную величину, однако, имеет один недостаток. По функции распределения трудно судить о характере распределения случайной величины в небольшой окрестности той или иной точки числовой оси
Определение. Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x) – первая производная от функции распределения F(x).
Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприемлема.
Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина Х в некоторой окрестности точки х при повторении опытов.
После введения функций распределения и плотности распределения можно дать следующее определение непрерывной случайной величины.
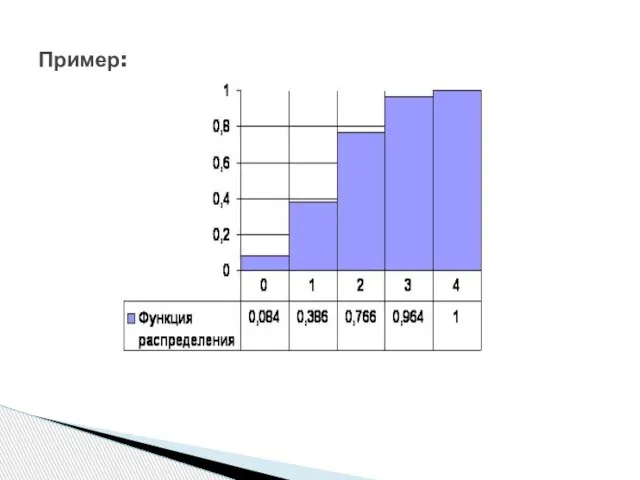
Плотность распределения:

Определение. Случайная величина Х называется непрерывной, если ее функция распределения F(x) непрерывна на всей оси ОХ, а плотность распределения f(x) существует везде, за исключением( может быть, конечного числа точек.
Зная плотность распределения, можно вычислить вероятность того, что некоторая случайная величина Х примет значение, принадлежащее заданному интервалу.
Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a, b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b.
Геометрически это означает, что вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (a, b), равна площади криволинейной трапеции, ограниченной осью ОХ, кривой распределения f(x) и прямыми x=a и x=b.

Функция распределения может быть легко найдена, если известна плотность распределения, по формуле:

Свойства плотности распределения:
Плотность распределения – неотрицательная функция.
Несобственный интеграл от плотности распределения в пределах от - ¥ до ¥ равен единице

Пример. Случайная величина подчинена закону распределения с плотностью:
Требуется найти коэффициент а, построить график функции плотности распределения, определить вероятность того, что случайная величина попадет в интервал от 0 до
Построим график плотности распределения: