Data Mining Ассоциативные правила

Цель данного метода — исследование взаимной связи между событиями, которые происходят совместно.
Разновидностью аффинитивного анализа является анализ рыночной корзины (market basket analysis), цель которого — обнаружить ассоциации между различными событиями, то есть найти правила для количественного описания взаимной связи между двумя или более событиями.

Примерами приложения ассоциативных правил могут быть следующие задачи:
выявление наборов товаров, которые в супермаркетах часто покупаются вместе или никогда не покупаются вместе;
определение доли клиентов, положительно относящихся к нововведениям в их обслуживании;
определение профиля посетителей веб-ресурса;
определение доли случаев, в которых новое лекарство показывает опасный побочный эффект.

Базовые понятия
транзакция — некоторое множество событий, происходящих совместно.
предметный набор — это непустое множество предметов, появившихся в одной транзакции.

ассоциативное правило формулируется в виде: «Если условие, то следствие».
Условие может ограничиваться только одним предметом
(left-hand side — LHS) и (right-hand side — RHS) компоненты

Показатели
Поддержка ассоциативного правила — это число транзакций, которые содержат как условие, так и следствие.

Показатели
Достоверность ассоциативного правила A → B представляет собой меру точности правила и определяется как отношение количества транзакций, содержащих и условие, и следствие, к количеству транзакций, содержащих условие:

Значимость ассоциативных правил
Если условие и следствие независимы, то поддержка правила примерно соответствует произведению поддержек условия и следствия, то естьSAB ≈ SASB
Пример с товарами и автомобилем ВАЗ

Дополнительные показатели
Лифт — это отношение частоты появления условия в транзакциях, которые также содержат и следствие, к частоте появления следствия в целом.
L(A → B) = C(A → B) / S(B).
L>1, связь положительная
L=1 связь отсутствует
L<1 связь отрицательная

НО!
Правило с меньшей поддержкой и большим лифтом может быть менее значимым, чем альтернативное правило с большей поддержкой и меньшим лифтом, потому что последнее применяется для большего числа покупателей.

Дополнительные показатели
Левередж — это разность между наблюдаемой частотой, с которой условие и следствие появляются совместно (то есть поддержкой ассоциации), и произведением частот появления (поддержек) условия и следствия по отдельности. Предложена Г. Пятецким-Шапиро.
T(A → B) = S(A → B) – S(A)S(B).

Если в базе данных транзакций присутствует k предметов и все ассоциации являются бинарными (то есть содержат по одному предмету в условии и следствии), то потребуется проанализировать k · 2k –1 ассоциаций.

Алгоритм Apriori

Частый предметный набор — предметный набор с поддержкой больше заданного порога либо равной ему. Этот порог называется минимальной поддержкой.

Методика поиска
1 Следует найти частые наборы.
2 На их основе необходимо сгенерировать ассоциативные правила, удовлетворяющие условиям минимальной поддержки и достоверности.

свойство антимонотонности
если предметный набор Z не является частым, то добавление некоторого нового предмета A к набору Z не делает его более частым.
Т.е. , если Z не является частым набором, то и набор Z U A также не будет являться таковым.

Набор транзакций D
F1 = {спаржа, фасоль, капуста, кукуруза, перец, кабачки, помидоры}

Создание множеств Fk
алгоритм Apriori сначала создает множество Fk кандидатов в k- предметные наборы путем связывания множества Fk – 1 с самим собой. Затем Fk сокращается с использованием свойства антимонотонности.

Множества F2

Генерация множеств F3
Для этого нужно связать наборы из множества F2 между собой,, если у них первые k – 1 предметов общие.
{спаржа, фасоль} + {спаржа, кабачки} = {спаржа, фасоль, кабачки}

Теперь F3 также сокращается с помощью свойства антимонотонности. Для каждого предметного набора s из множества F3 создаются и проверяются поднаборы размером k – 1.

Генерация ассоциативных правил
1 Генерируются все возможные поднаборы s
2 Если поднабор ss является непустым поднабором s, то рассматривается ассоциативное правило R: ss → (s – ss), где s – ss представляет собой набор s без поднабора ss.

{спаржа, фасоль, кабачки}
и {фасоль, кукуруза, помидоры}
Для первого ассоциативного правила ss = {спаржа, фасоль}, и тогда (s – ss) = {кабачки}

Иерархические ассоциативные правила

S(I) ≥ S(ij),
где I — группа в иерархии,
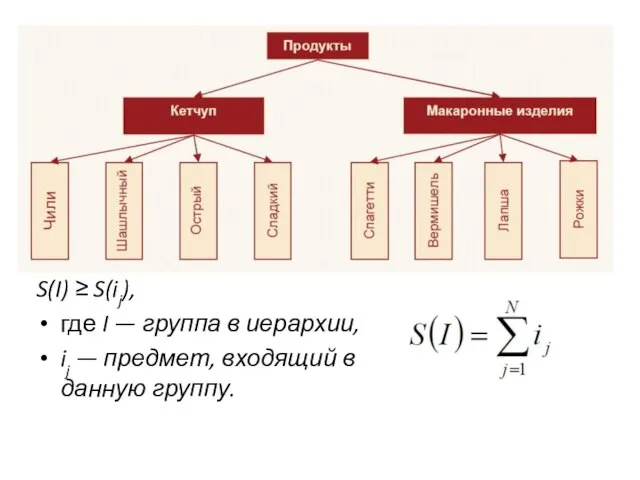
ij — предмет, входящий в данную группу.

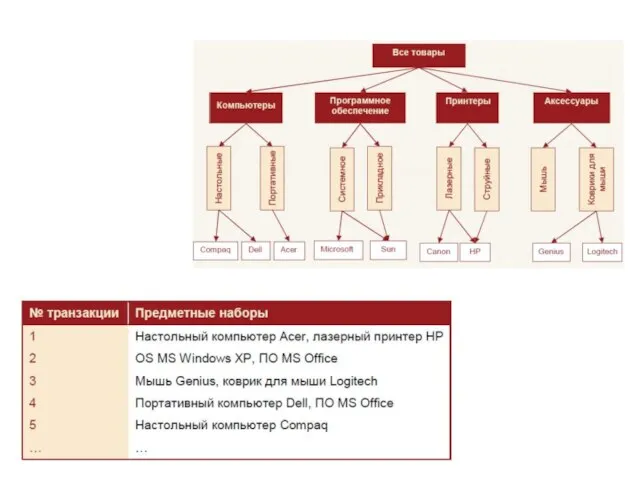
Ассоциативные правила, обнаруженные для предметов, расположенных на различных иерархических уровнях, получили название иерархические ассоциативные правила.
В зарубежной литературе они также известны как многоуровневые правила (multilevel rules) или обобщенные правила (generalized rules).

1 Сначала ищутся ассоциации с высокой поддержкой для верхних уровней иерархии.
2 Анализируются потомки только тех предметов верхних уровней, которые удовлетворяют заданному минимуму поддержки Smin. Анализ потомков тех предметов, которые сами по себе являются редкими, не имеет смысла, поскольку они будут встречаться еще реже, чем их предки.

Методы поиска иерархических ассоциативных правил
Вариант 1 — использование одинакового порога минимальной поддержки Smin на всех иерархических уровнях.

Маловероятно, что предметы нижних уровней продаются так же часто, как предметы более высоких уровней.
Если Smin слишком большой, это может привести к потере полезных ассоциаций между предметами низких уровней.
Если Smin слишком низкий, это может породить много неинтересных ассоциаций между предметами высоких уровней.

Вариант 2 — использование пониженного порога минимальной поддержки для нижних уровней иерархии

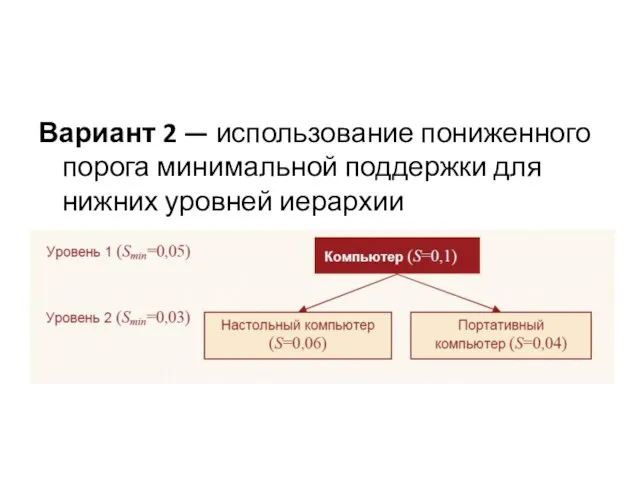
Вариант 3 — независимая установка порога.
Межуровневая (cross-level) фильтрация по одному предмету.
Предмет на i-м уровне проверяется тогда и только тогда, когда его родительский узел на уровне i – 1 содержит частые наборы.