Дифференциал и интеграл

Функция. Предел функции
Функцией называется соответствие при котором каждому значению x из некоторого множества D (D∈R) сопоставляется по некоторому правилу единственное число y, зависящее от x
y= f(x)
x – аргумент функции (независимая переменная)
y – значение функции f (зависимая переменная)
D – область определения функции D (f) – все значения x
Все значения y – область значений функции f , E (f)

Графиком функции называется множество точек плоскости с координатами (x; y), где x пробегает всю область определения функции f
Способы задания функции
Аналитический (рекуррентный) – формула
Графический – график функции
Табличный – таблица зависимости x и y

Рассмотрим интервал с центром в точке x0 и радиусом r
Окрестностью точки x0 радиуса r называется интервал с центром в точке x0 радиуса r, δ(x0)
Если рассматривается окрестность без самой точки x0, то она называется проколотой °δ(x0)

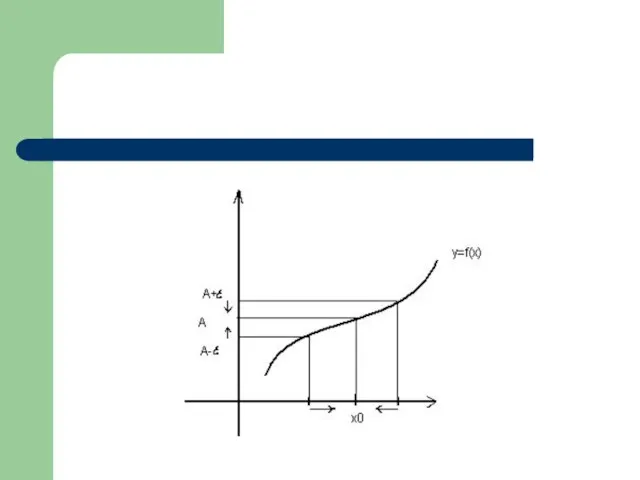
Предел функции
Число A называется пределом функции f(x) в точке x0, если для любого числа ε>0, существует окрестность δ>0, такая, что выполняется неравенство|f(x)-A|<ε, для любого x из окрестности δ(x0)
−ε
A−ε

Теоремы о пределах
Теорема о единственности предела: если предел функции существует, то он единственный (число A)
Теорема о пределе суммы: если существуют пределы функций f(x) и g(x), то существует предел их суммы равный сумме пределов функций f(x) и g(x)

Теорема о пределе произведения: если существуют пределы функций f(x) и g(x), то существует предел их произведения равный произведению пределов функций f(x) и g(x)
Теорема о пределе частного: если существуют пределы функций f(x) и g(x) и предел функции g(x) не равен нулю, то существует предел их частного равный частному пределов функций f(x) и g(x)

Следствия из теорем
Следствие 1: постоянный множитель можно вынести за знак предела
Следствие 2: если n натуральное число, то

Следствие 3: предел многочлена
равен значению многочлена в точке x0 при
Следствие 4: предел дробно –рациональной функции
равен значению этой функции в точке x0 при
если x принадлежит области определения функции

Пример:

Производная функции и дифференциал
Производная функции – это предел отношения приращения функции к приращению аргумента, когда приращения аргумента стремится к нулю

Свойства производной
Теорема: производная суммы, произведения, частного вычисляются по следующим формулам:

Производная сложной функции:
Пример:

Таблица производных

Дифференциал функции
Нахождение производной называется дифференцированием
Дифференциал – это произведение производной функции на приращение аргумента функции y = f(x)
dy = f'(x)Δx
Рассмотрим функцию y = x, тогда y'= 1 ⇒ dx = Δx ⇒
dy = f'(x)dx ⇒ (отношение дифференциалов)

Свойства дифференциала
Дифференциал функции – это главная часть её приращения
Дифференциал функции – это линейная функция приращения аргумента или касательная к графику функции ⇒ геометрически dy = f'(x)dx - уравнение касательной в системе координат (dx; dy) ⇒

Вычисление дифференциала функции
Пример.

Применение дифференциала к приближенным вычислениям
Для функции y=f(x) и точки x0 можно приближенно вычислить значение функции в точке x близкой к x0, если знать приращение функции Δy на [x0; x], то точное значение функции f(x) = y0+ Δy, где y0 значение функции в точке x0
Приближенные формулы основаны на замене приращения функции Δy её дифференциалом dy
Δy = f(x) - y0
f(x) - y0 ≈ f '(x0) Δx
f(x) ≈ y0+ dy ≈ y0 + f '(x0)(x – x0)

Для y = xn
(x0+ Δx)n ≈ x0n + nx0n-1Δx
Пример:

Первообразная функции и интеграл
Первообразная и неопределенный интеграл
Свойства неопределенного интеграла
Таблица первообразных
Методы интегрирования: непосредственное, замена переменной, интегрирование по частям
Определенный интеграл. Формула Ньютона – Лейбница
Применение определенного интеграла: вычисление площади фигуры, длины дуги, объема тела
Дифференциальные уравнения. Уравнения с разделяющимися переменными