Презентация на тему Гармонические колебания. гармонический осцилятор. Пружинный физический и математический маятники
Содержание
- 2. 5. Механические колебания и волны 5.1. Гармонические колебания и их характеристики Колебаниями называются движения или процессы,
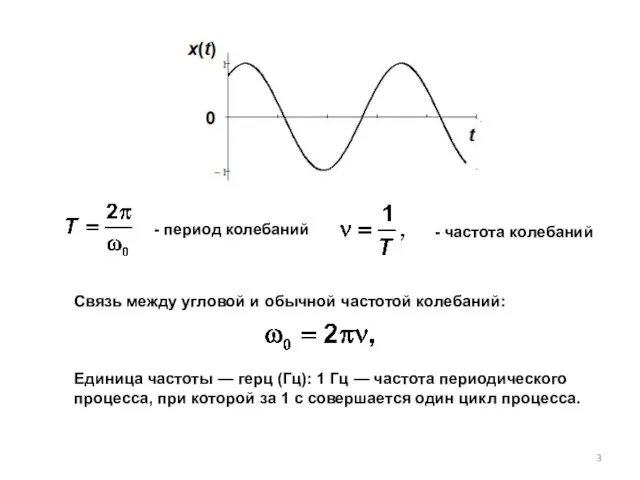
- 3. - период колебаний - частота колебаний Связь между угловой и обычной частотой колебаний: Единица частоты —
- 4. Дифференциальное уравнение гармонических колебаний: Решение дифференциального уравнения:
- 5. Вещественная часть вектора: Гармонические колебания можно графически представить в виде вращающегося вектора:
- 6. 5.2. Гармонический осциллятор. Пружинный, физический и математический маятники Гармоническим осциллятором называется система, совершающая колебания, описываемые уравнением
- 7. Уравнение движения маятника: Пружинный маятник совершает гармонические колебания по закону: с циклической частотой Потенциальная энергия пружинного
- 8. 2. Физический маятник — это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной
- 9. Уравнение динамики физического маятника: или: где: Решение динамического уравнения:
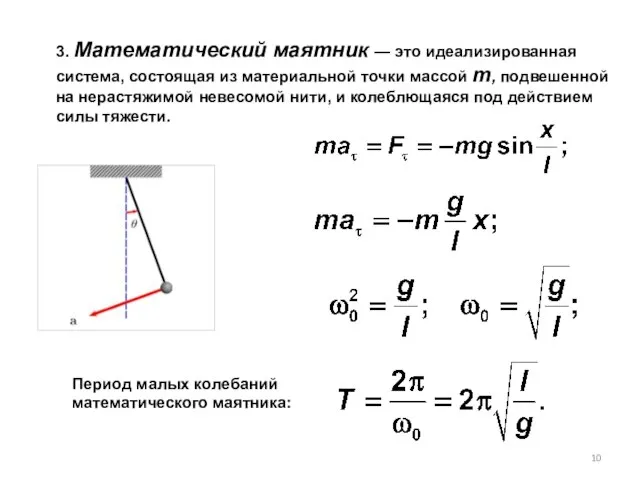
- 10. 3. Математический маятник — это идеализированная система, состоящая из материальной точки массой т, подвешенной на нерастяжимой
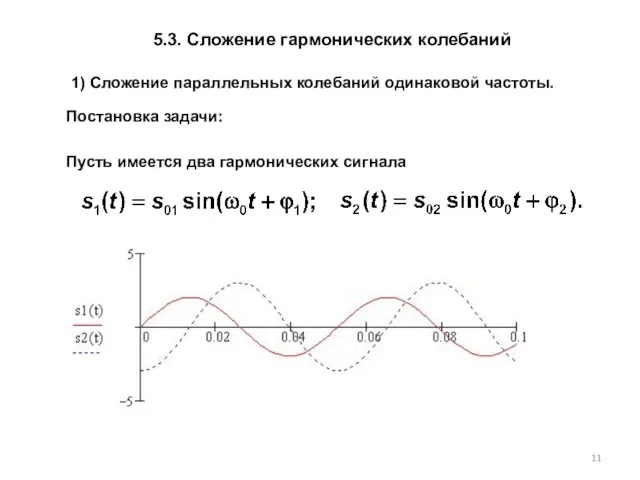
- 11. 1) Сложение параллельных колебаний одинаковой частоты. Пусть имеется два гармонических сигнала Постановка задачи: 5.3. Сложение гармонических
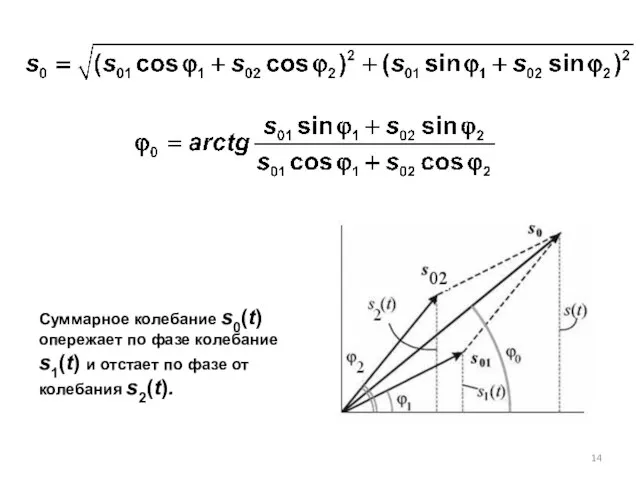
- 12. Необходимо сложить два колебания с одинаковыми частотами:
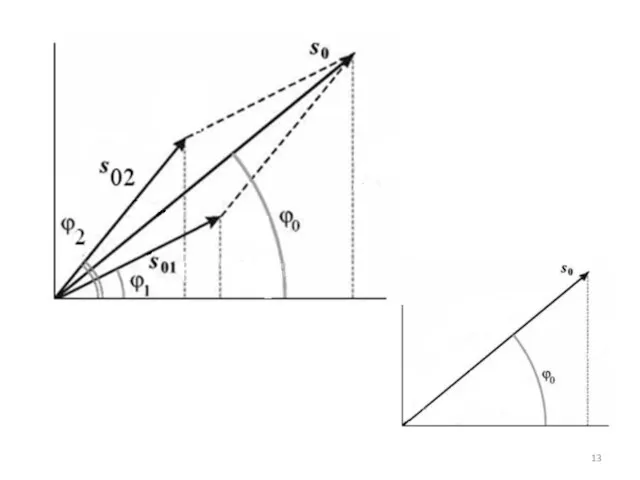
- 14. Суммарное колебание s0(t) опережает по фазе колебание s1(t) и отстает по фазе от колебания s2(t).
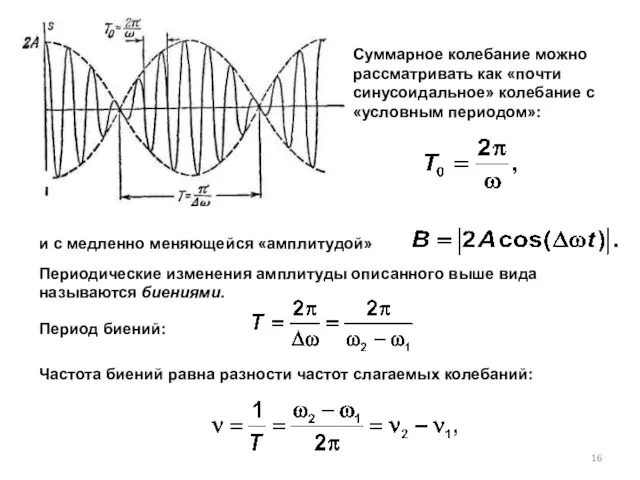
- 15. 2) Сложение параллельных гармонических колебаний с близкими частотами. Найдем сумму двух гармонических колебаний, частоты которых различны,
- 16. Суммарное колебание можно рассматривать как «почти синусоидальное» колебание с «условным периодом»: и с медленно меняющейся «амплитудой»
- 17. Чтобы получить траекторию движения, исключим из выражений текущее время и преобразуем синус по формулам тригонометрии: 3)
- 18. Умножим первое уравнение на cos φ2, а второе — на cos φ1 и вычтем второе уравнение
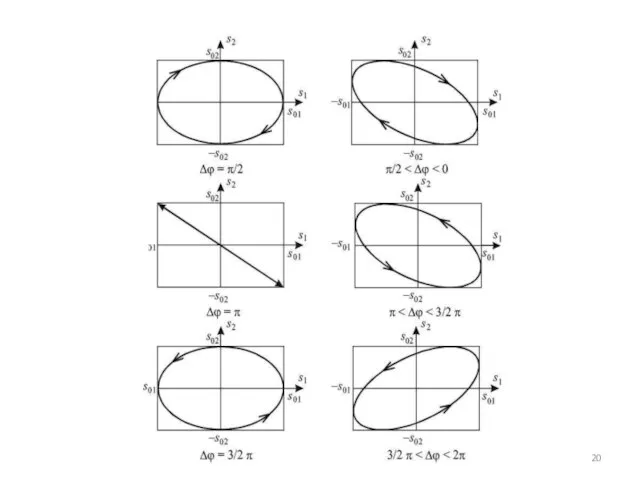
- 19. В результате будут совершатьcя периодические движения по эллиптической траектории. Направление движения вдоль траектории и ориентация эллипса
- 22. Скачать презентацию












 «ДЕТИ ИМЕЮТ ПРАВО НА ОСОБУЮ ЗАБОТУ И ПОМОЩЬ»
«ДЕТИ ИМЕЮТ ПРАВО НА ОСОБУЮ ЗАБОТУ И ПОМОЩЬ» Система права и система законодательства
Система права и система законодательства Мир Леонардо да Винчи (1452-1519)
Мир Леонардо да Винчи (1452-1519) Урок-консультация по теме « Решение показательных уравнений».
Урок-консультация по теме « Решение показательных уравнений». Белорусская кухня
Белорусская кухня Сущность жизни и свойства живого. Уровни организации живой материи
Сущность жизни и свойства живого. Уровни организации живой материи Интернет-трейдинг на рынке стандартных контрактовММВБ
Интернет-трейдинг на рынке стандартных контрактовММВБ Перспектива
Перспектива Право в системе социальных норм. 10 класс
Право в системе социальных норм. 10 класс Гулькевичи - мой родной город
Гулькевичи - мой родной город Тоталитаризм. Виды тоталитаризма
Тоталитаризм. Виды тоталитаризма Рейтинг надежности микрофинансовой организации: возможности и преимущества
Рейтинг надежности микрофинансовой организации: возможности и преимущества Презентация на тему COMMUNICATION COMMUNICATION TECHNOLOGIES
Презентация на тему COMMUNICATION COMMUNICATION TECHNOLOGIES  Организация соревнований по эстафетному бегу. Круговая, встречная, линейная, комбинированная, эстафета Веселые старты
Организация соревнований по эстафетному бегу. Круговая, встречная, линейная, комбинированная, эстафета Веселые старты Общение. Значение общения. Роль общения в профессиональной деятельности
Общение. Значение общения. Роль общения в профессиональной деятельности Дополнительная образовательнаяПРОГРАММА«Тяжелая атлетика»(физкультурно-спортивная направленность)
Дополнительная образовательнаяПРОГРАММА«Тяжелая атлетика»(физкультурно-спортивная направленность) Земноводные. Места обитания и внешнее строение
Земноводные. Места обитания и внешнее строение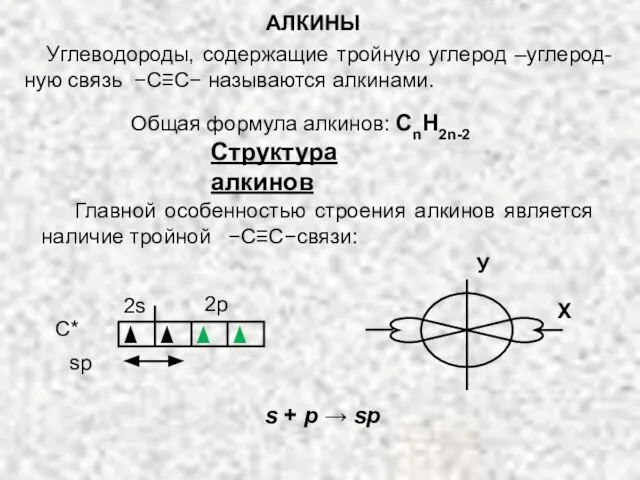 Структура алкинов
Структура алкинов Мосты в искусстве
Мосты в искусстве Презентация на тему Водно-электролитные нарушения и их коррекция
Презентация на тему Водно-электролитные нарушения и их коррекция  ИК пассивные детекторы IR100/120
ИК пассивные детекторы IR100/120 Вікно, двері, багатоповерхівка
Вікно, двері, багатоповерхівка ИСПОЛЬЗОВАНИЕ ПМК «ИНФОРМАЦИОННАЯ КУЛЬТУРА»
ИСПОЛЬЗОВАНИЕ ПМК «ИНФОРМАЦИОННАЯ КУЛЬТУРА» Model Checking
Model Checking Моя студенческая жизнь!
Моя студенческая жизнь! Поверхности вращения
Поверхности вращения Школа профессионального мастерства
Школа профессионального мастерства Әлифба. Ыы
Әлифба. Ыы