Слайд 2Геометрические задачи 7 класса в вариантах ОГЭ

Слайд 3
Цели урока:
Сегодня мы с вами разберём несколько примеров по

геометрии 7 класса, которые даются в ОГЭ-2015.
Ведь действительно, Основной Государственный Экзамен — ОГЭ, рассчитан не только на знания 9 класса, но и на те знания, которые ученики получают в 7 и 8 классах по геометрии, и, начиная с 5 класса, по математике и алгебре.
Поэтому, в модуле «Геометрия» есть задачи из курса 7 класса.
Слайд 4 Задача 1.
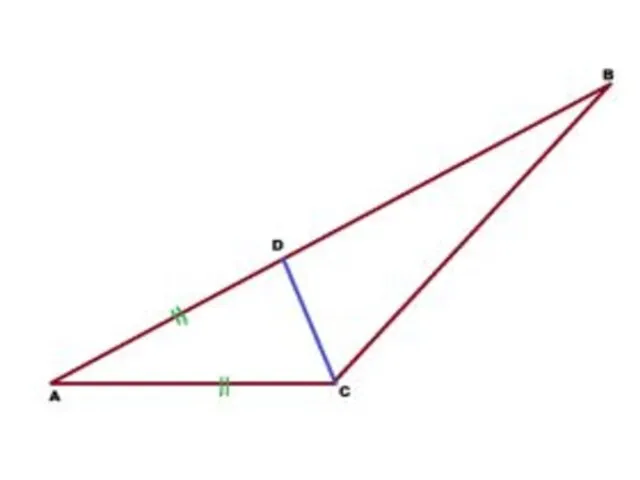
В треугольнике АВС точка D на стороне АВ выбрана

так, что АС=AD. Угол А треугольника АВС равен 16°, а угол АСВ равен 134°. Найти угол DCB.
Слайд 6 Решение: Из треугольника ADC видно, что он равнобедренный, поскольку 2 боковые стороны

его равны.
А в равнобедренном треугольнике углы при основании равны.
Значит, угол ADC равен углу АСВ.
Но сумма внутренних углов треугольника равна 180°.
Отсюда, сумма двух углов при основании равна 180-16=164°.
Углы, как мы уже сказали, равны. Поэтому, каждый из них равен 164:2 = 82°.
Угол АСВ по условию равен 134°.
А если внутри угла провести луч, то он разделит угол на 2 угла, сумма градусных мер которых будет равна градусной мере первоначального угла.
Т.е. Угол АСВ равен сумме углов АCD и DCB.
Отсюда, угол DCB равен 134 — 82 = 52°.
Ответ: угол DCB равен 52°.
Слайд 7 Задача 2.
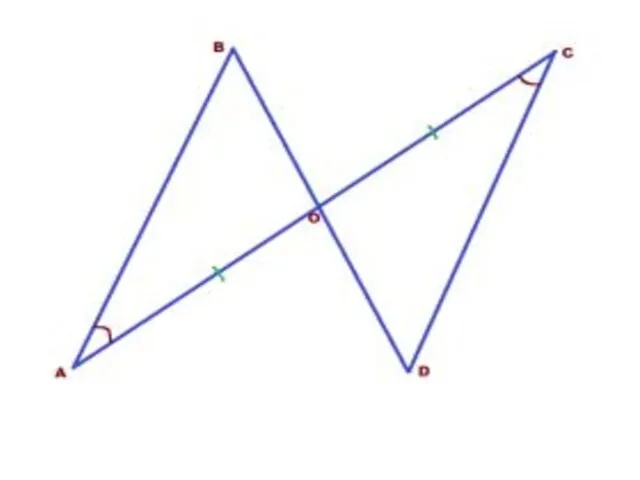
Два отрезка АС и BD пересекают в точке О.

Причём, АО=СО и ∠А=∠С. Доказать, что треугольники АОВ и OC равны.
Слайд 9 Доказательство: В искомых треугольниках есть по одной равной стороне и одному равному

углу. Значит, согласно признакам равенства треугольников, нам необходимо ещё либо по одной равной стороне, либо по одному равному углу.
Стороны как-то не проглядываются, а вот по равному углу можно ещё найти.
Углы АОВ и DOC — вертикальные.
А вертикальные углы, как мы знаем, равны.
В каждом из треугольников мы имеем по равной стороне и двум равным углам, прилежащим к ней.
Треугольники равны по 2 признаку.
Слайд 10 Задача 3.
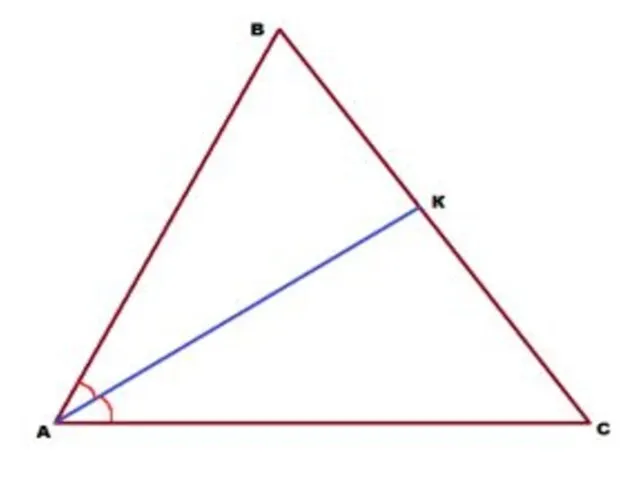
В треугольнике АВС проведена биссектриса АК. Угол АКС равен

94°, а угол АВС равен 62°. Найти угол С треугольника АВС.
Слайд 12 Решение: Угол АКС является внешним для треугольника АВК и равным сумме двух внутренних

углов, не смежных с ним, т.е. сумме углов В и ВАК.
Отсюда мы можем найти угол ВАК.
Он равен 94 — 62 = 32°.
Поскольку АК — биссектриса угла А, то угол КАС тоже равен 32°.
А теперь, рассматривая треугольник АКС и зная в нём 2 угла, можно найти третий.
∠С = 180 — 32 — 94 = 54°.
Ответ: угол С равен 54°.
Слайд 13 Задача 4.
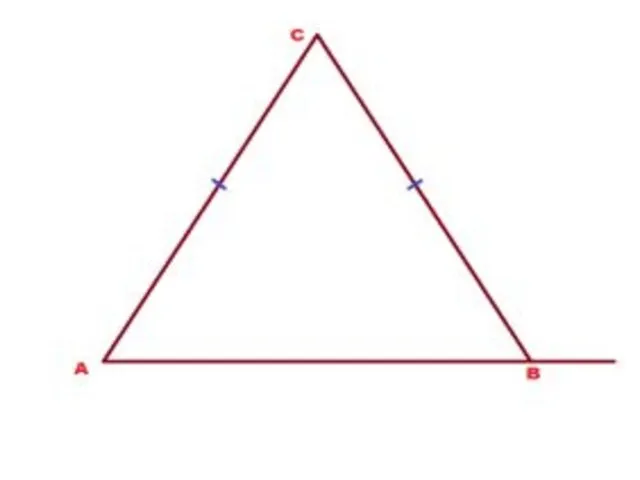
В треугольнике АВС боковые стороны АС и АВ

равны между собой. Внешний угол при вершине В равен 110°. Найти угол С.
Слайд 15 Решение: Внешний угол В равен 110°, значит, смежный с ним внутренний

угол в треугольнике равен
180-10 = 70°.
Но внутренний угол В равен углу А, как углы при основании равнобедренного треугольника. Значит, угол А равен 70°.
А сумма внутренних углов треугольника равна 180°.
И если 2 из них равны по 70, то на долю третьего угла С приходится 180 — 70 — 70 = 40°.
Ответ: угол с равен 40°.
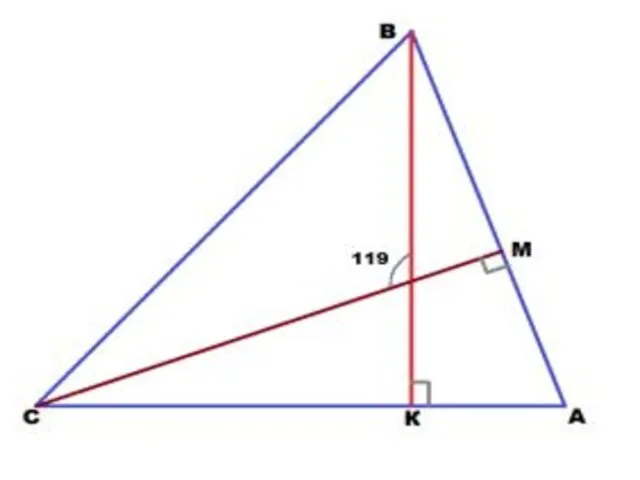
Слайд 16 Задача 5.
В треугольнике АВС проведены высоты, которые пересекаются в точке

О. Угол СОВ равен 119°. Найти угол А.
Слайд 18 Решение:
Угол ВОМ смежный углу СОМ и равен 180-119 = 61°.
Угол

СМА внешний в треугольнике СМВ и равен сумме двух внутренних, не смежных с ним.
Отсюда, угол ОВМ равен 90-61 = 29°.
А из прямоугольного треугольника ВКА можно найти угол А, т.к. сумма острых углов в прямоугольном треугольнике равна 90°.
Значит, угол А равен 90 — 29 = 61°.
Ответ: угол А равен 61°.












 Гвоздок. Мелкобытовые и отделочные работы
Гвоздок. Мелкобытовые и отделочные работы Презентация на тему Holidays USA (Праздники в США)
Презентация на тему Holidays USA (Праздники в США) Системно - деятельностный подход в обучении
Системно - деятельностный подход в обучении Угольная промышленность
Угольная промышленность Ломоносов
Ломоносов Курск и Новгород. Опись иллюстраций
Курск и Новгород. Опись иллюстраций Политика как призвание и профессия
Политика как призвание и профессия «Новая технология динамического наблюдения за больными АГ с использованием средств мобильной связи»
«Новая технология динамического наблюдения за больными АГ с использованием средств мобильной связи» ЯЗЫК HTML (продолжение)
ЯЗЫК HTML (продолжение)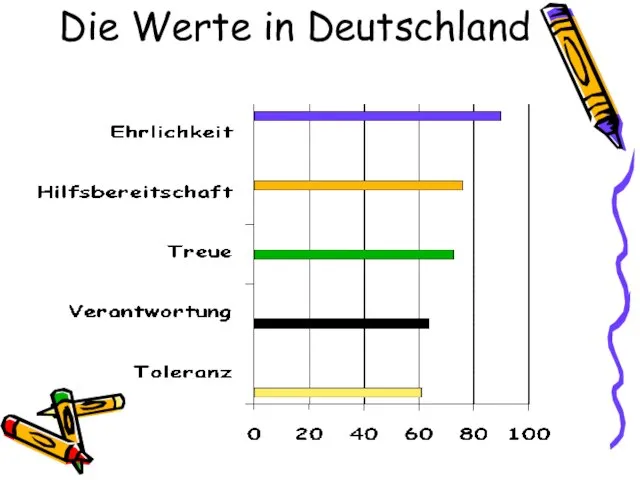 Die Werte in Deutschland
Die Werte in Deutschland 23 февраля - День Защитника Отечества
23 февраля - День Защитника Отечества Тобольский Индустриальный институт
Тобольский Индустриальный институт Презентация на тему Спектры и спектральный анализ
Презентация на тему Спектры и спектральный анализ  Проект "Мой выбор"
Проект "Мой выбор" Реализация Федерального государственного образовательного стандарта нового поколения в Забайкальском крае
Реализация Федерального государственного образовательного стандарта нового поколения в Забайкальском крае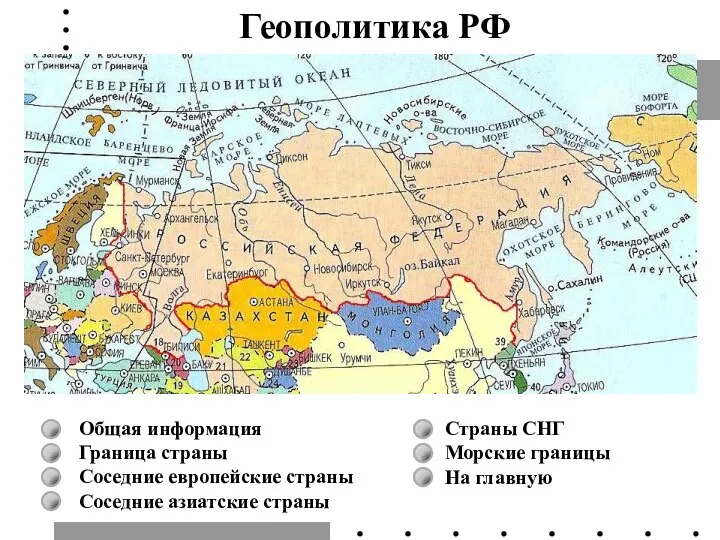 Геополитика РФ
Геополитика РФ Аппликация из цветной бумаги Осенний пейзаж
Аппликация из цветной бумаги Осенний пейзаж Моделирование нелинейных свойств конструкций
Моделирование нелинейных свойств конструкций Бадминтон
Бадминтон Интеллектуальные продукты и система государственных закупок
Интеллектуальные продукты и система государственных закупок Хĕлле. Хуравне туп
Хĕлле. Хуравне туп СИСТЕМА «КАДРЫ»версия 3.3
СИСТЕМА «КАДРЫ»версия 3.3 Об экспериментальной работе по введению профильного обучения
Об экспериментальной работе по введению профильного обучения Новодевичий Монастырь
Новодевичий Монастырь Бейсбол
Бейсбол звездный час
звездный час Содержание урока
Содержание урока Техника эстафетного бега: прием- передача эстафетной палочки
Техника эстафетного бега: прием- передача эстафетной палочки