Презентация на тему Компьютерное моделирование

НЕКОТОРЫЕ ОБЛАСТИ ПРИМЕНЕНИЯ КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ
вычисление производных и интегралов
механика точки
механика системы материальных точек
механика твердого тела
расчет электрических цепей
расчет электрического и магнитного полей
моделирование массопереноса и теплопроводности
волновые и автоволновые процессы
расчет течения жидкости
моделирование биологических процессов
клеточные автоматы
множество мандельброта и другие фракталы

Математические модели: особенности
Выбор модели исходя из имеющейся информации о явлении, процессе или устройстве
Аналитическое или численное моделирование
Выбор численного метода
Дискретная модель
Программа для компьютера
Процесс моделирования
Анализ результатов
Уточнение модели или выбор новой

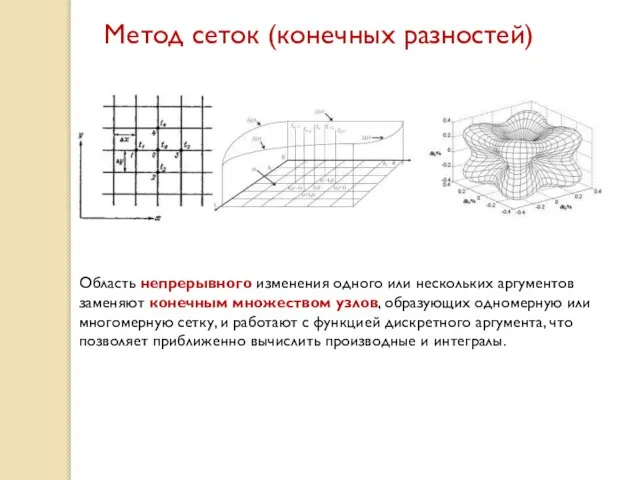
Метод сеток (конечных разностей)
Область непрерывного изменения одного или нескольких аргументов заменяют конечным множеством узлов, образующих одномерную или многомерную сетку, и работают с функцией дискретного аргумента, что позволяет приближенно вычислить производные и интегралы.

Примеры простых математических моделей некоторых природных процессов
Кинетика химических реакций
Можно представить себе одностадийную химическую реакцию типа А ->В, где А – исходное вещество, В – конечный продукт. Если A – концентрация вещества , то ее убывание часто описывают уравнением:
dA/dt=-kA ,
где k – константа скорости реакции, а начальное условие задается как A=Ao при t = 0. Если k = const, уравнение легко интегрируется:
A=Aoexp(-kt).
Аналогичной формулой описывается закон радиоактивного распада:
N=Noexp(- аt),
где No– начальная концентрация распадающегося радиоактивного вещества, а - постоянная распада.

Зачастую одностадийные химические реакции бывают обратимыми. Тогда для их математического описания потребуются два уравнения реакций: прямой и обратной.
dA/dt= - k12A+ k21B
dB/dt= - k21B+ k12A
Модель типа жертва-хищник
Пусть популяция кроликов будет жертвами, популяция лис – хищниками. Предположим, что кроме кроликов лисы ничего не едят (и потому не размножаются), а в отсутствие лис кролики размножаются неограниченно. В этом случае скорость увеличения популяции кроликов будет
dx/dt=ax,
скорость уменьшения популяции лис
dy/dt=-py,
где t– время, a– коэффициент рождаемости кроликов, р– коэффициент смертности лис.

Однако популяции взаимодействуют (парные взаимодействия, включающие произведение xy). Тогда для кроликов
dx/dt=ax - bxy,
где b – коэффициент, учитывающий уменьшение популяции кроликов вследствие поедания их лисами.
Для лис:
dy/dt=-py + cxy,
где с – коэффициент, учитывающий прирост популяции лис вследствие поедания ими кроликов.
Для решения системы должны быть заданы начальные размеры популяций, а для получения правдоподобного результата – правдоподобные значения всех коэффициентов.

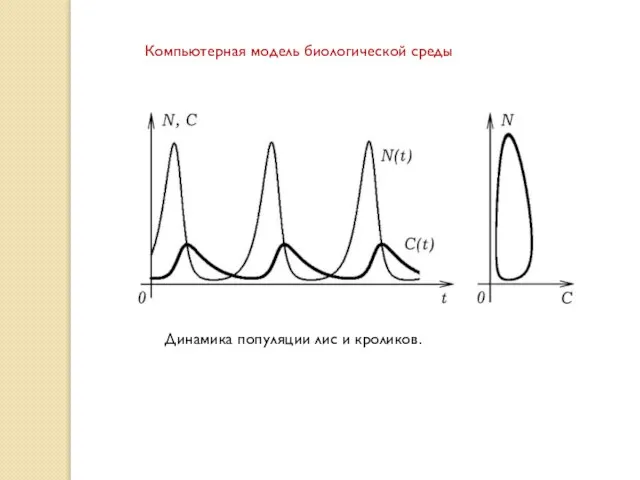
Динамика популяции лис и кроликов.
Компьютерная модель биологической среды

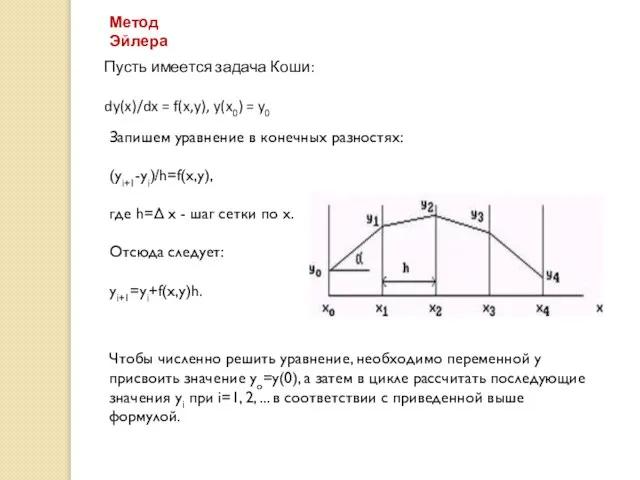
Метод Эйлера
Пусть имеется задача Коши:
dy(x)/dx = f(x,y), y(x0) = y0
Запишем уравнение в конечных разностях:
(yi+1-yi)/h=f(x,y),
где h=Δ x - шаг сетки по x.
Отсюда следует:
yi+1=yi+f(x,y)h.
Чтобы численно решить уравнение, необходимо переменной y присвоить значение yo=y(0), а затем в цикле рассчитать последующие значения yi при i=1, 2, ... в соответствии с приведенной выше формулой.

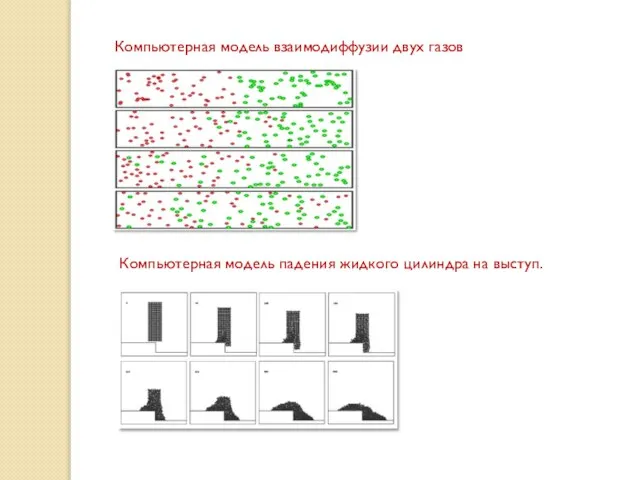
Компьютерная модель взаимодиффузии двух газов
Компьютерная модель падения жидкого цилиндра на выступ.

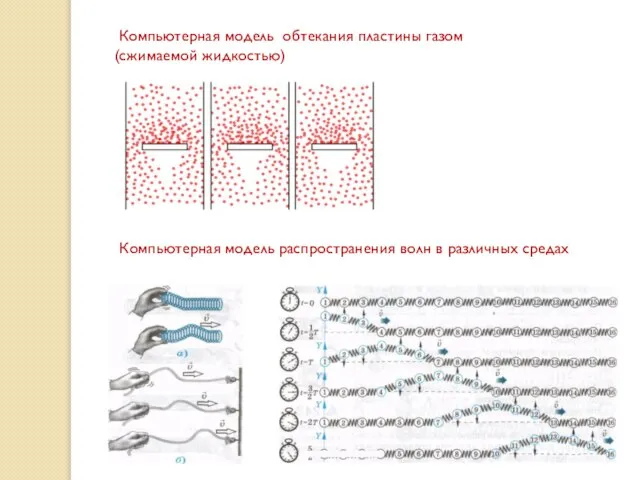
Компьютерная модель обтекания пластины газом (сжимаемой жидкостью)
Компьютерная модель распространения волн в различных средах

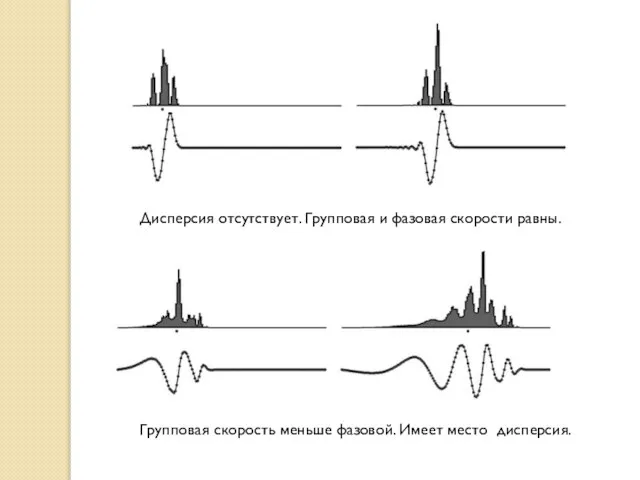
Дисперсия отсутствует. Групповая и фазовая скорости равны.
Групповая скорость меньше фазовой. Имеет место дисперсия.

Отражение и прохождение волны через границу раздела двух сред.

Двумерная волна: прохождение через границу раздела двух сред(моделируется дифракция).
Увеличение и уменьшение интенсивности колебания в зависимости от фазы(моделируется интерференция).

Не все так просто
Важное отличительное свойство описанного движения состоит в том, что, несмотря на сложный характер, оно предсказуемо. Иными словами, начальное измерение содержит информацию, которой можно воспользоваться для прогноза будущего поведения.
Вопрос: всегда ли так бывает?
В 1963 году американский метеоролог из Массачусетского технологического института Эдвард Лоренц задался вопросом: почему стремительное совершенствование компьютеров не привело к воплощению в жизнь мечты метеорологов – достоверному среднесрочному (на 2-3 недели вперед) прогнозу погоды?

В 1963 году Рэй Брэдбери описал
«эффект бабочки». Согласно этому эффекту малые причины могут иметь большие следствия. Математики называют это свойство чувствительностью к начальным данным. Поведение такого типа называется динамическим хаосом
Системы с динамическим хаосом порождают клубок траекторий (непредсказуемые и невоспроизводимые типы поведения в ограниченных рамках).
Такие клубки классики нелинейной науки Д. Рюэль и Ф. Такенс в 1971 году назвали странными аттракторами.
Переход системы из одной траектории развития к другой определяется точкой (областью) бифуркации.
В основе теории хаоса лежит математический аппарат, описывающий поведение некоторых нелинейных динамических систем подверженных при определённых условиях явлению, известному как хаос. Поведение такой системы кажется случайным, даже если модель, описывающая систему, является детерминированнной.

Бифурка́ция — термин происходит от лат. bifurcus — «раздвоенный» и употребляется в широком смысле для обозначения всевозможных качественных перестроек или метаморфоз различных объектов при изменении параметров, от которых они зависят.

Случайное слабое внешнее воздействие или слабые флуктуации внутренних параметров, "приуроченные" к определенному моменту развития системы, могут привести к большим ее внутренним изменениям.
Флуктуации возникают хаотично, их огромное количество, но большинство из них затухает, как бы отсекаются все лишние вихревые потоки, остаются только те, которые образуют новые устойчивые макросостояния (структуры) - аттракторы. Аттрактор как бы притягивает к себе множество траекторий развития системы, определяемых разными начальными значениями параметров, создавая своеобразный конус.

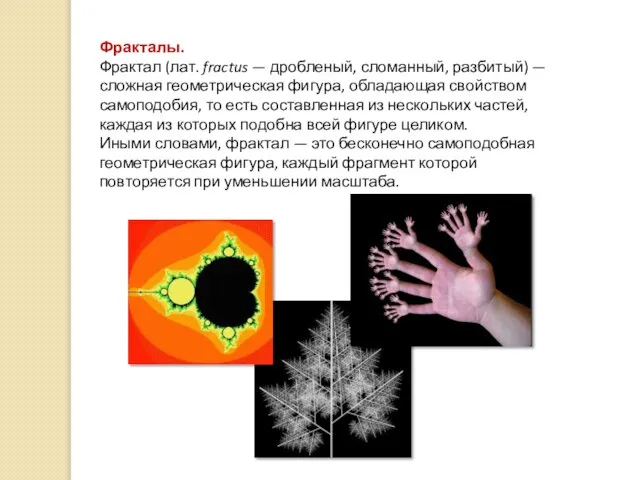
Фракталы.
Фрактал (лат. fractus — дробленый, сломанный, разбитый) — сложная геометрическая фигура, обладающая свойством самоподобия, то есть составленная из нескольких частей, каждая из которых подобна всей фигуре целиком.
Иными словами, фрактал — это бесконечно самоподобная геометрическая фигура, каждый фрагмент которой повторяется при уменьшении масштаба.

Термин «фрактал» был введён
Бенуа Мандельбротом в 1975 г. и получил широкую популярность с выходом в 1977 г. его книги «Фрактальная геометрия природы»:
«Почему геометрию часто называют холодной и сухой? Одна из причин заключается в ее неспособности описать форму облака, горы, дерева или берега моря. Облака - это не сферы, горы - не конусы, линии берега - это не окружности, и кора не является гладкой, и молния не распространяется по прямой. Природа демонстрирует нам не просто более высокую степень, а совсем другой уровень сложности.»

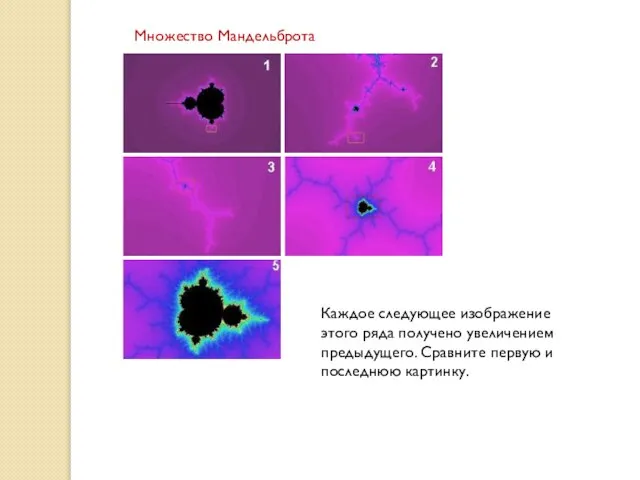
Каждое следующее изображение этого ряда получено увеличением предыдущего. Сравните первую и последнюю картинку.
Множество Мандельброта

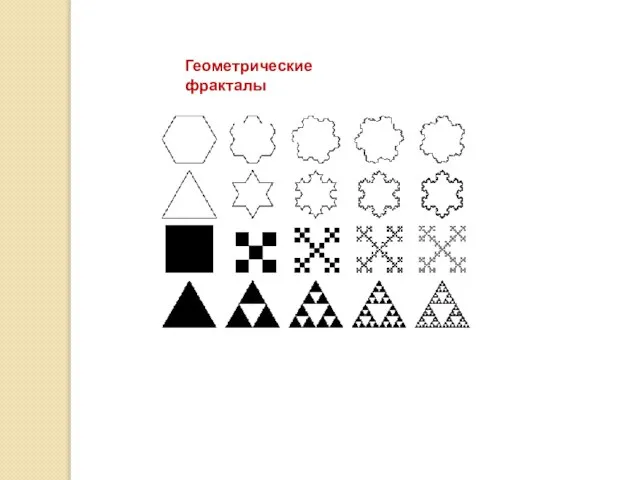
Геометрические фракталы

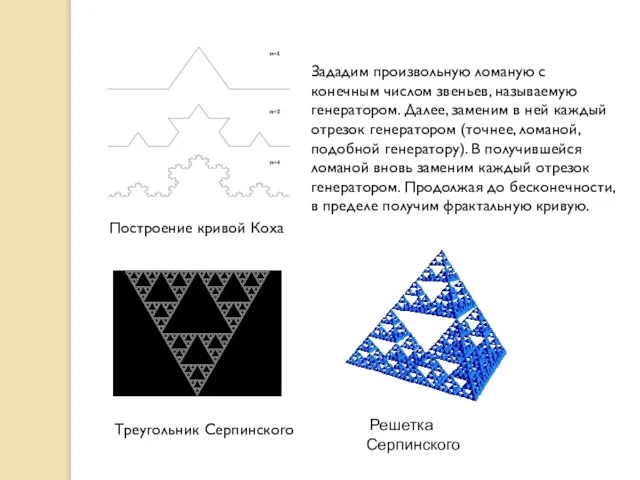
Построение кривой Коха
Зададим произвольную ломаную с конечным числом звеньев, называемую генератором. Далее, заменим в ней каждый отрезок генератором (точнее, ломаной, подобной генератору). В получившейся ломаной вновь заменим каждый отрезок генератором. Продолжая до бесконечности, в пределе получим фрактальную кривую.
Треугольник Серпинского
Решетка Серпинского

Кривая Пеано (1-5 итерации). Ее уникальность в том, что она заполняет всю плоскость. Доказано, что для каждой точки на плоскости можно найти точку, принадлежащую линии Пеано.

Лазер (англ. laser, акроним от англ. light amplification by stimulated emission of radiation — усиление света посредством вынужденного излучения), оптический квантовый генератор — устройство, преобразующее энергию накачки (световую, электрическую, тепловую, химическую и др.) в энергию когерентного, монохроматического, поляризованного и узконаправленного потока излучения.
Физической основой работы лазера служит квантовомеханическое явление вынужденного (индуцированного) излучения.
Квантовая электроника
Лазеры

Все лазеры состоят из трёх основных частей:
-активной (рабочей) среды;
-системы накачки (источник энергии);
-оптического резонатора
Для усиления света необходимо, чтобы возбуждённых атомов в среде было больше, чем невозбуждённых (так называемая инверсия населённостей). В состоянии термодинамического равновесия это условие не выполняется, поэтому используются различные системы накачки активной среды лазера (оптические, электрические, химические и др.).
Первоисточником генерации является процесс спонтанного излучения, поэтому для обеспечения преемственности поколений фотонов необходимо существование положительной обратной связи, за счёт которой излучённые фотоны вызывают последующие акты индуцированного излучения. Для этого активная среда лазера помещается в оптический резонатор.

Различные виды лазерных устройств

Волоконная оптика
Волоконная оптика (fiber optics) - это раздел оптики, в котором рассматривается передача света и изображения по светопроводам и волноводам оптического диапазона, в частности по многожильным световодам и пучкам гибких волокон.

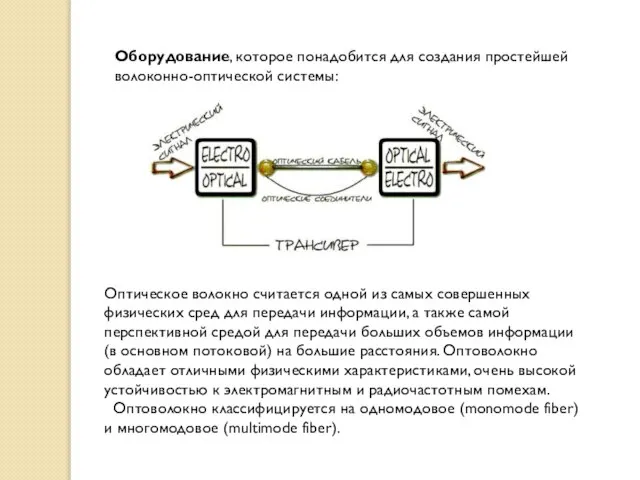
Оборудование, которое понадобится для создания простейшей волоконно-оптической системы:
Оптическое волокно считается одной из самых совершенных физических сред для передачи информации, а также самой перспективной средой для передачи больших объемов информации (в основном потоковой) на большие расстояния. Оптоволокно обладает отличными физическими характеристиками, очень высокой устойчивостью к электромагнитным и радиочастотным помехам.
Оптоволокно классифицируется на одномодовое (monomode fiber) и многомодовое (multimode fiber).

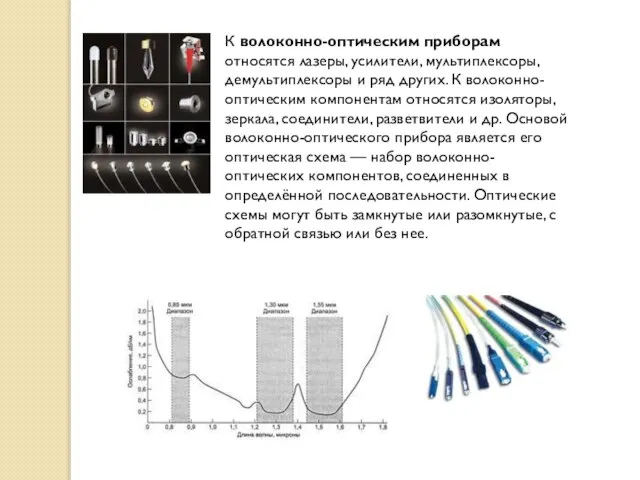
К волоконно-оптическим приборам относятся лазеры, усилители, мультиплексоры, демультиплексоры и ряд других. К волоконно-оптическим компонентам относятся изоляторы, зеркала, соединители, разветвители и др. Основой волоконно-оптического прибора является его оптическая схема — набор волоконно-оптических компонентов, соединенных в определённой последовательности. Оптические схемы могут быть замкнутые или разомкнутые, с обратной связью или без нее.

Цветовое зрение
В глазу человека содержатся два типа светочувствительных клеток (рецепторов): высокочувствительные палочки, отвечающие за сумеречное (ночное) зрение, и менее чувствительные колбочки, отвечающие за цветное зрение.
В сетчатке глаза человека есть три вида колбочек, максимум чувствительности которых приходится на красный, зелёный и синий участок спектра, то есть соответствует трем «основным» цветам.
Равномерное раздражение всех трёх элементов, соответствующее средневзвешенному дневному свету, также вызывает ощущение белого цвета . Трёхсоставную теорию цветового зрения впервые высказал в 1756 году М. В. Ломоносов, когда писал «о трёх материях дна ока».

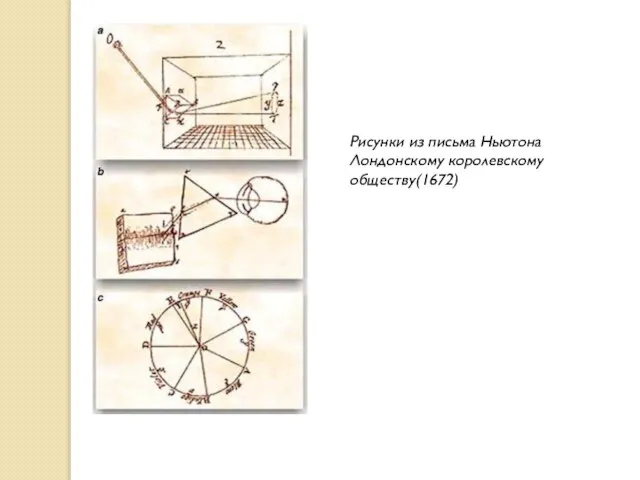
Рисунки из письма Ньютона
Лондонскому королевскому
обществу(1672)

Окружности или спирали?
Обработка зрительной информации мозгом
Из-за большого числа этапов процесса зрительного восприятия его отдельные характеристики рассматриваются с точки зрения разных наук — оптики (в т.ч. биофизики), психологии, физиологии, химии (биохимии). На каждом этапе восприятия возникают искажения, ошибки, сбои, но мозг человека обрабатывает полученную информацию и вносит необходимые коррективы. Эти процессы носят неосознаваемый характер и реализуются в многоуровневой автономной корректировке искажений. Так устраняются сферическая и хроматическая аберрации, эффекты слепого пятна, проводится цветокоррекция, формируется стереоскопическое изображение и т. д. В тех случаях, когда подсознательная обработка информации недостаточна, или же избыточна, возникают оптические иллюзии.

Психологическая иллюзия «уткозаяц».
Оптическая иллюзия: соломинка кажется сломанной.
Физиологическая иллюзия: Видны несуществующие черные точки

Иллюзия восприятия цвета:
метка на "светлом" параллелограмме кажется ярче и светлее, чем метка на "тёмном"
Центральная полоса вся одной яркости

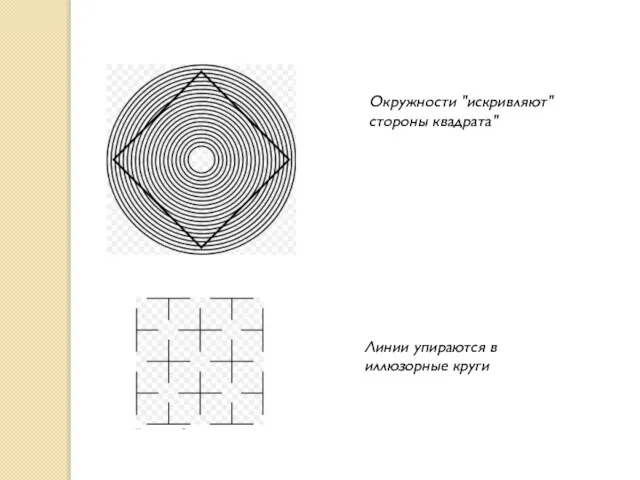
Окружности "искривляют" стороны квадрата"
Линии упираются в иллюзорные круги

Иллюзорные треугольники
Эффект появления треугольников разного размера в разных местах решетки

Иллюзия движения. Следует смотреть на чёрную точку в центре и двигать головой вперёд-назад. Круги вокруг точки начнут двигаться

Пристально смотрите на шар в центре.
Кажется, что узор на нем движется из стороны в сторону?
Не отрывая взгляда от центра круга, подвигайте головой.
Возникла иллюзия, что узор вокруг шара сдвигается?

Видите волны? Это не анимация, а статическая картинка!

Смотрите в центр рисунка и подвигайте головой вперед назад. Окружности на рисунке превратятся в движущиеся спирали.