Презентация на тему Механика жидкостей Эффект Доплера

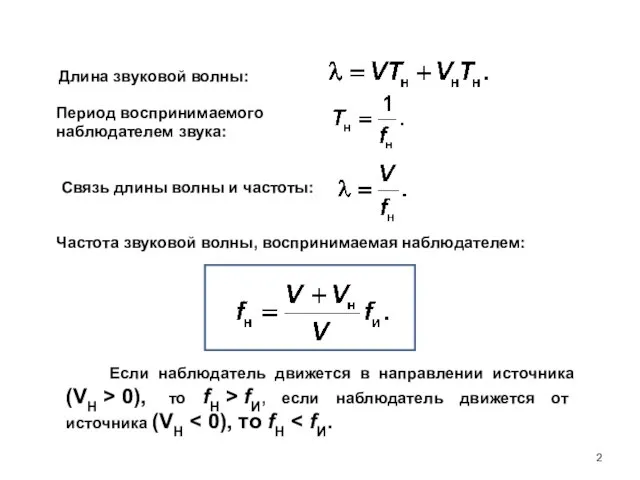
Длина звуковой волны:
Период воспринимаемого наблюдателем звука:
Связь длины волны и частоты:
Частота звуковой волны, воспринимаемая наблюдателем:
Если наблюдатель движется в направлении источника (VН > 0), то fН > fИ, если наблюдатель движется от источника (VН < 0), то fН < fИ.

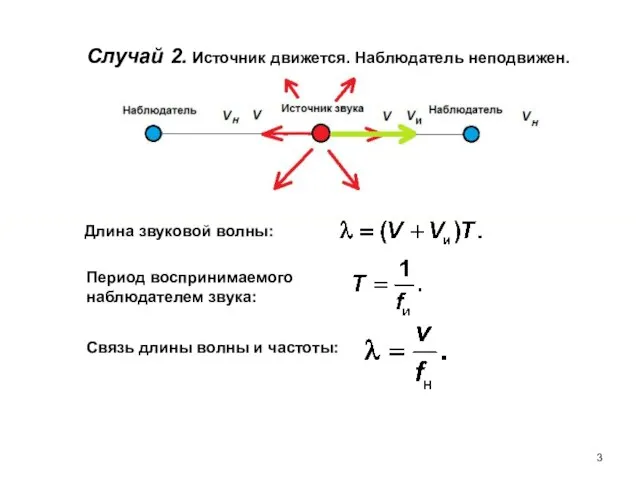
Случай 2. Источник движется. Наблюдатель неподвижен.
Длина звуковой волны:
Период воспринимаемого наблюдателем звука:
Связь длины волны и частоты:

Частота звуковой волны, воспринимаемая наблюдателем:
Если источник удаляется от наблюдателя, то Vи > 0 и, следовательно, fН < fИ. Если источник приближается к наблюдателю, то Vи < 0 и fН > fИ.

Эффект Доплера объясняется тем, что при движении источника звука или наблюдателя длина волны и частота звука могут существенно изменяться.
Случай 3. Источник и наблюдатель движутся со скоростями Vи и Vн, формула для эффекта Доплера приобретает вид:

6. Элементы механики жидкостей
В газе молекулы совершают беспорядочное, хаотическое движение. В результате соударений они стремятся разлететься во все стороны, заполняя весь предоставленный им объем.
Жидкость, имея определенный объем, принимает форму того сосуда, в который она заключена. В жидкостях в отличие от газов среднее расстояние между молекулами остается практически постоянным, поэтому жидкость обладает практически неизменным объемом.
При исследовании свойств жидкости используется физическая модель несжимаемой жидкости, плотность которой всюду одинакова и не меняется со временем.
6.1. Давление жидкостей и газов

На каждый элемент поверхности тела, помещенного в жидкость действует сила, направленная перпендикулярно поверхности.
Давлением жидкости называется физическая величина, определяемая нормальной силой, действующей со стороны жидкости на единицу площади:
Единица давления — паскаль (Па):
1 Па равен давлению, создаваемому силой 1 Н, равномерно распределенной по нормальной к ней поверхности площадью 1 м2
(1 Па=1 Н/м2).
Давление жидкости подчиняется закону Паскаля.
Закон Паскаля:
«давление в любом месте покоящейся жидкости одинаково по всем направлениям, причем давление одинаково передается по всему объему, занятому покоящейся жидкостью».

При равновесии жидкости давление по горизонтали всегда одинаково. Поэтому свободная поверхность покоящейся жидкости всегда горизонтальна вдали от стенок сосуда.
Если жидкость несжимаема, то ее плотность не зависит от давления. Тогда при поперечном сечении S столба жидкости, его высоте h и плотности ρ вес будет равен:
Давление ρ g h называется гидростатическим давлением.
Давление на нижнее основание:

где ρ — плотность жидкости, V— объем погруженного в жидкость тела.
«на тело, погруженное в жидкость (газ), действует со стороны этой жидкости направленная вверх выталкивающая сила, равная весу вытесненной телом жидкости (газа)»:
Закон Архимеда:

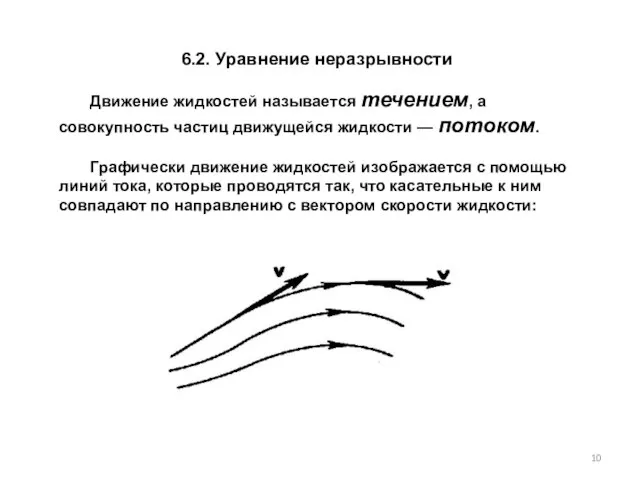
6.2. Уравнение неразрывности
Движение жидкостей называется течением, а совокупность частиц движущейся жидкости — потоком.
Графически движение жидкостей изображается с помощью линий тока, которые проводятся так, что касательные к ним совпадают по направлению с вектором скорости жидкости:

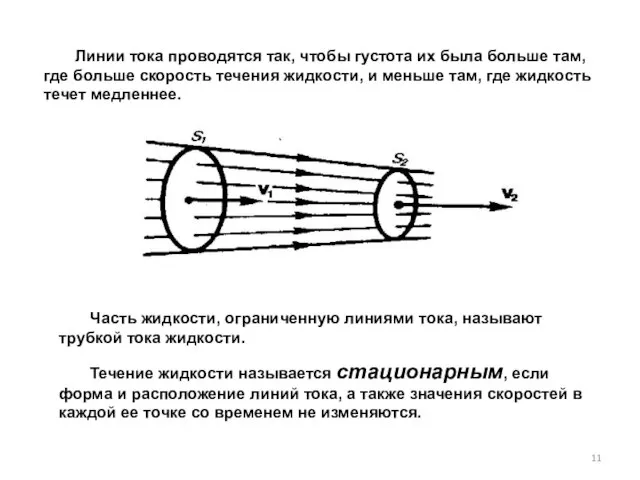
Линии тока проводятся так, чтобы густота их была больше там, где больше скорость течения жидкости, и меньше там, где жидкость течет медленнее.
Часть жидкости, ограниченную линиями тока, называют трубкой тока жидкости.
Течение жидкости называется стационарным, если форма и расположение линий тока, а также значения скоростей в каждой ее точке со временем не изменяются.

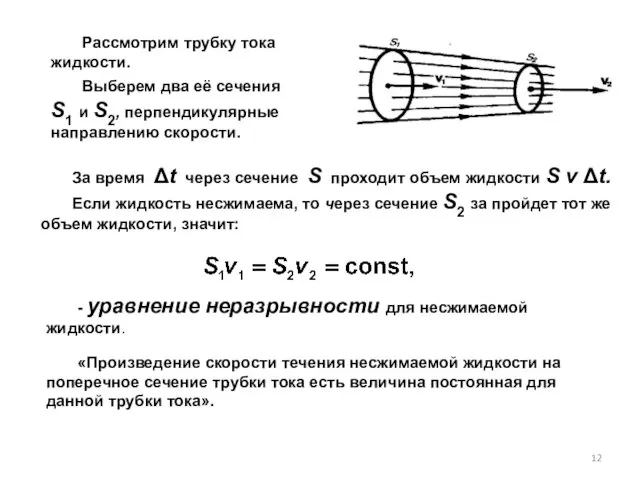
Рассмотрим трубку тока жидкости.
Выберем два её сечения S1 и S2, перпендикулярные направлению скорости.
За время Δt через сечение S проходит объем жидкости S v Δt.
Если жидкость несжимаема, то через сечение S2 за пройдет тот же объем жидкости, значит:
- уравнение неразрывности для несжимаемой жидкости.
«Произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки тока».

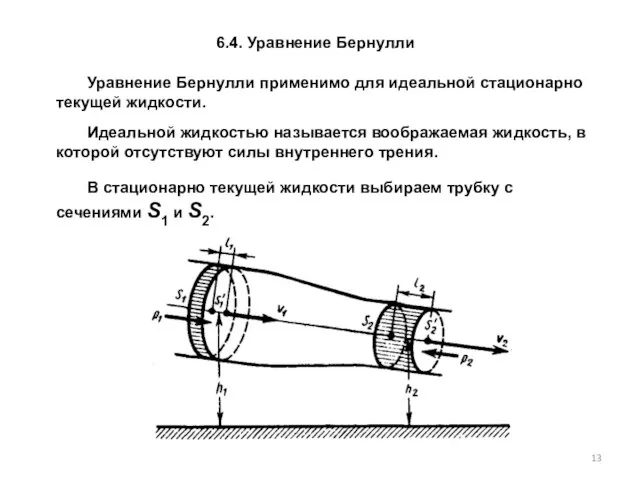
6.4. Уравнение Бернулли
Идеальной жидкостью называется воображаемая жидкость, в которой отсутствуют силы внутреннего трения.
В стационарно текущей жидкости выбираем трубку с сечениями S1 и S2.
Уравнение Бернулли применимо для идеальной стационарно текущей жидкости.

Согласно закону сохранения энергии, изменение полной энергии E2—E1 идеальной несжимаемой жидкости должно быть равно работе А внешних сил по перемещению массы m жидкости:
С другой стороны работа внешних сил равна сумме:
Приравняем записанные выражения и получим равенство:

Даниил Бернулли - швейцарский физик и математик (1700—1782).
Разделим записанное равенство на ΔV:
— это уравнением Бернулли.
Согласно уравнению непрерывности:

Из уравнения Бернулли для горизонтальной трубки тока и уравнения нераз­рывности следует:
При течении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жидкости больше в местах сужения.
Статическое давле­ние больше в более широких местах, т. е. там, где скорость меньше.
Уравнение Бернулли выражает закон сохранения энергии применительно к устано­вившемуся течению идеальной жидкости.
Величина р в уравнении Бернулли называется статическим давлением,
величина ρ v2 / 2 — динамическим давлением,
величина ρ g h — гидростатическим давлением.

6.5. Вязкость (внутреннее трение)
Вязкость — это свойство реальных жидкостей оказывать сопротив­ление перемещению одной части жидкости относительно другой.
При перемещении одних слоев реальной жидкости относительно других возникают силы внутреннего трения, направленные по касательной к поверхности слоев.
- градиент скорости.
Он показывает, как быстро меняется скорость при переходе от слоя к слою в направлении х, перпендикулярном направле­нию движения слоев.
Со стороны слоя, движущегося быстрее, на слой, движущийся медлен­нее, действует ускоряющая сила.
Со стороны слоя, движущегося медленнее, на слой, движущийся быстрее, действует тормозящая сила.

Сила внутреннего трения:
Коэффициент пропорциональности , зависящий от природы жидкости, называется динамической вязкостью
(или просто вязкостью).
Единица вязкости — паскаль-секунда (Па⋅с):
1 Па⋅с равен динамической вязкости среды, в которой при ламинарном течении и градиенте скорости с модулем, равным 1 м/с на 1 м, возникает сила внутреннего трения 1 Н на 1 м2 поверхности касания слоев (1 Па⋅с= 1 Н⋅с/м2).
Вязкость зависит от температуры, причем характер этой зависимости для жидкостей и газов различен (для жидкостей η с увеличе­нием температуры уменьшается, у газов, наоборот, увеличивается).

6.6. Два режима течения жидкостей.
Течение называется ламинарным (слоистым), если вдоль потока каждый выделенный тонкий слой скользит относительно соседних, не перемешиваясь с ними.
Ламинарное течение жидкости наблюдается при небольших скоростях ее движения. Внешний слой жидкости, примыкающий к поверхности трубы, в которой она течет, из-за сил молекулярного сцепления прилипает к ней и остается неподвижным.
Скоро­сти последующих слоев тем больше, чем больше их расстояние до поверхности трубы, и наибольшей скоростью обладает слой, движущийся вдоль оси трубы.

При турбулентном течении частицы жидкости приобретают составляющие скоростей, перпендикулярные течению, поэтому они могут переходить из одного слоя в другой.
Скорость частиц жидкости быстро возрастает по мере удаления от поверхности трубы, затем изменяется довольно незначительно. Так как частицы жидкости переходят из одного слоя в другой, то их скорости в различных слоях мало отличают­ся.
Из-за большого градиента скоростей у поверхности трубы обычно происходит образование вихрей.
Течение называется турбулентным (вихревым), если вдоль потока происходит интенсивное вихреобразование и перемешивание жидкости (газа).

Характер течения определяется числом Рейнольдса:
Рейнольдс Осборн— английский ученый: физик и механик (1842—1912) .
ν = η/ρ — кинематическая вязкость,
ρ — плотность жидкости,
— средняя по сечению трубы скорость жидкости,
d — характерный линейный размер, например диаметр трубы.

1. При малых значениях числа Рейнольдса:
наблюдается ламинарное тече­ние.
течение турбулентное.
происходит переход от ламинарного течения к турбулентному.
2. При средних значениях числа Рейнольдса:
3. При больших значениях числа Рейнольдса:

6.7. Метод Стокса (метод определения вязкости)
Метод определения вязкости основан на измерении скорости медленно движущихся в жидкости небольших тел сферической формы.
Джордж Стокс— английский физик и математик (1819—1903).

На шарик, падающий в жидкости вертикально вниз, действуют три силы:
сила тяжести Р = 4/3 π r 3 ρ g (ρ — плотность шарика),
сила Архимеда FA = 4/3 π r 3 ρ‘ g (ρ' — пло­тность жидкости),
сила сопротивления.
Сила сопротивления эмпирически установлена Джорджем Стоксом:
r — радиус шарика, v — скорость шарика.

6.8. Метод Пуазейля (метод определения вязкости)
Метод основан на ламинарном течении жидкости в тонком капилляре.
Жан Пуазейль (1799—1868) — французский физиолог и физик.

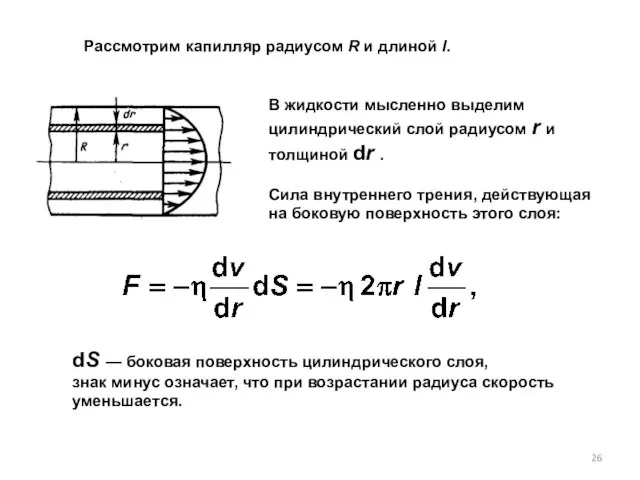
В жидкости мысленно выделим цилиндрический слой радиусом r и толщиной dr .
Сила внутреннего трения, действующая на боковую поверхность этого слоя:
dS — боковая поверхность цилиндрического слоя,
знак минус означает, что при возрастании радиуса скорость уменьшается.
Рассмотрим капилляр радиусом R и длиной l.

Для установившегося течения жидкости сила внутреннего трения, действующая на боковую поверхность цилиндра, уравновешивается силой давления, действующей на его основание:
После интегрирования, полагая, что у стенок имеет место прилипание жидкости, т. е. скорость на расстоянии R от оси равна нулю, получим:
Отсюда видно, что скорости частиц жидкости распределяются по параболическому закону, причем вершина параболы лежит на оси трубы.