Содержание
- 2. Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой
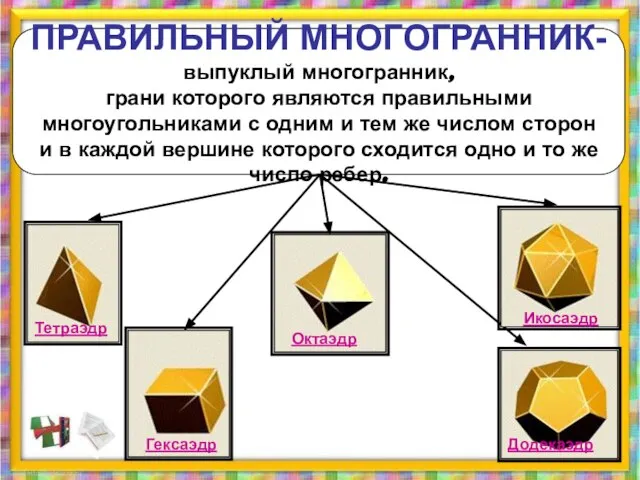
- 3. ПРАВИЛЬНЫЙ МНОГОГРАННИК- выпуклый многогранник, грани которого являются правильными многоугольниками с одним и тем же числом сторон
- 4. «эдра» - грань «тетра» - 4 «гекса» - 6 «окта» - 8 «икоса» - 20 «додека»
- 5. Тетраэдр – представитель правильных выпуклых многогранников. Поверхность тетраэдра состоит из четырех равносторонних треугольников, сходящихся в каждой
- 6. Куб или гексаэдр – представитель правильных выпуклых многогранников. Куб имеет шесть квадратных граней, сходящихся в каждой
- 7. Октаэдр – представитель семейства правильных выпуклых многогранников. Октаэдр имеет восемь треугольных граней, сходящихся в каждой вершине
- 8. Додекаэдр – представитель семейства правильных выпуклых многогранников. Додекаэдр имеет двенадцать пятиугольных граней, сходящихся в вершинах по
- 9. Икосаэдр – представитель семейства правильных выпуклых многогранников. Поверхность икосаэдра состоит из двадцати равносторонних треугольников, сходящихся в
- 10. Платон
- 11. огонь вода воздух земля вселенная тетраэдр икосаэдр октаэдр гексаэдр додекаэдр
- 12. Модель Солнечной системы Кеплера.
- 13. "Космический кубок" И.Кеплера
- 15. Икосаидро-додекаидровая структура Земли.
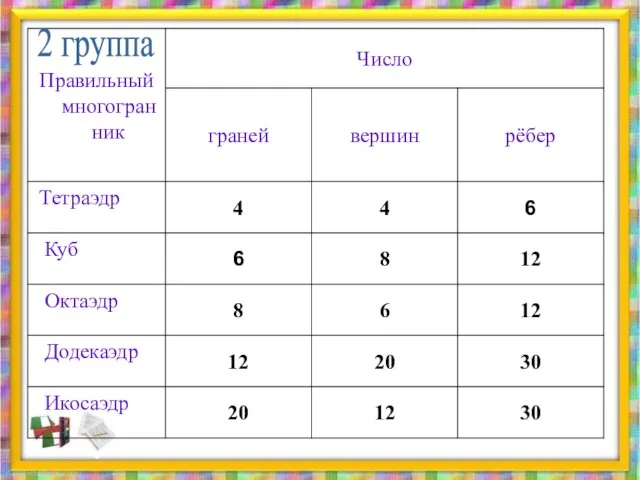
- 16. 1 группа- доказать, что правильных многогранников существует ровно 5. 2 группа- используя модели многогранников, заполнить данную
- 17. Вывод: Существует лишь пять выпуклых правильных многогранников – тетраэдр, октаэдр и икосаэдр с треугольными гранями, куб
- 18. 2 группа
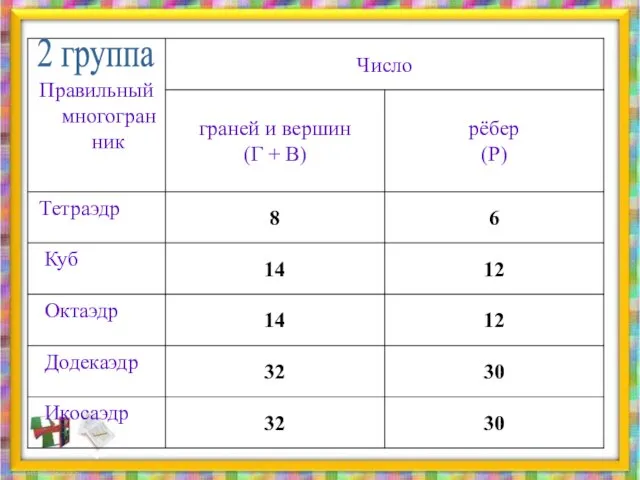
- 19. 2 группа
- 20. Теорема Эйлера Число вершин плюс число граней минус число рёбер равно двум. В + Г –
- 21. Леонард Эйлер (1707 – 1783 гг.) немецкий математик и физик
- 22. 3 группа
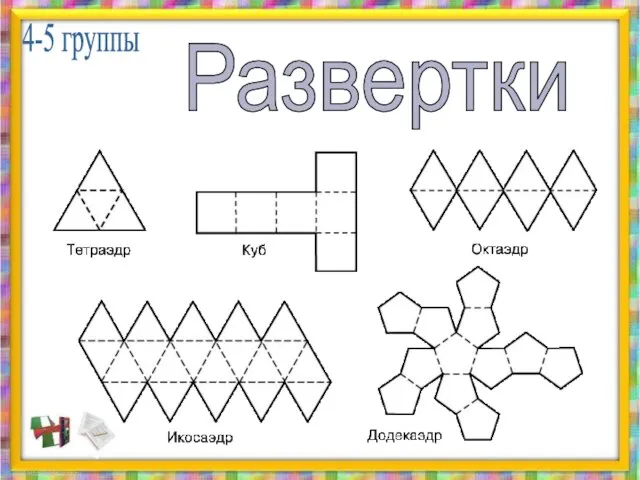
- 23. 4-5 группы Развертки
- 24. Архимедовыми телами называются полуправильные однородные выпуклые многогранники, то есть выпуклые многогранники, все многогранные углы которых равны,
- 25. Архимедовы тела
- 26. Французский математик Пуансо в 1810 году построил четыре правильных звездчатых многогранника: малый звездчатый додекаэдр, большой звездчатый
- 27. Малый звездчатый додекаэдр Большой звездчатый додекаэдр Большой икосаэдр Большой додекаэдр
- 28. Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины
- 29. Химия
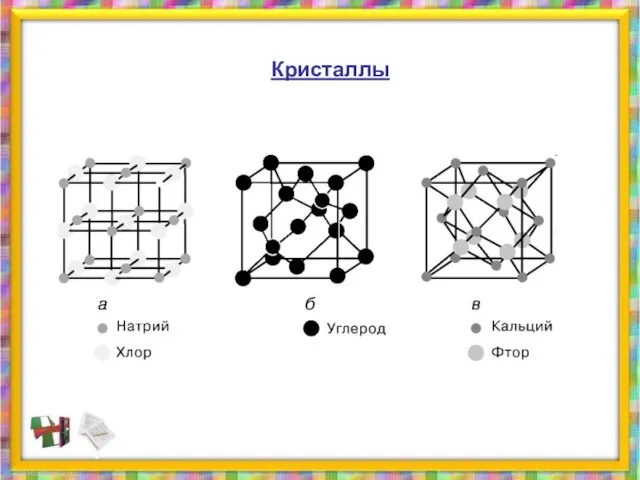
- 30. Кристаллы
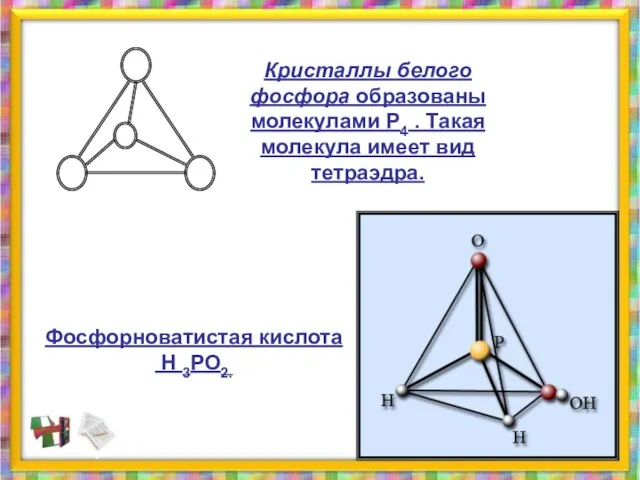
- 31. Кристаллы белого фосфора образованы молекулами Р4 . Такая молекула имеет вид тетраэдра. Фосфорноватистая кислота Н 3РО2.
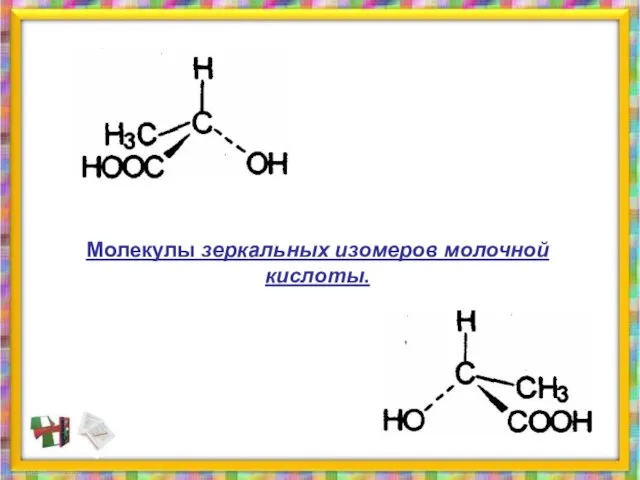
- 32. Молекулы зеркальных изомеров молочной кислоты.
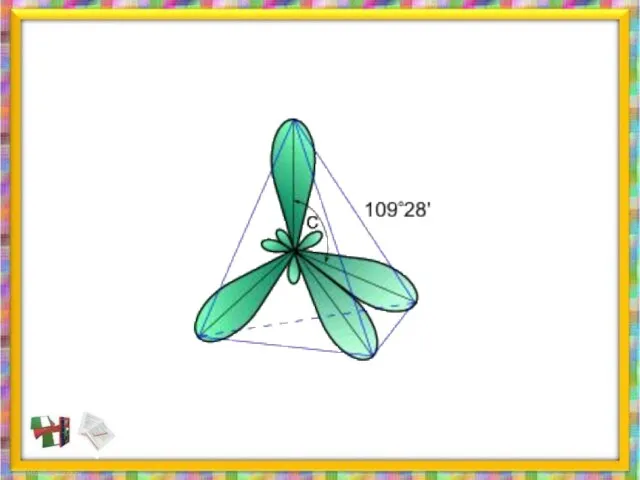
- 34. Строение молекулы метана .
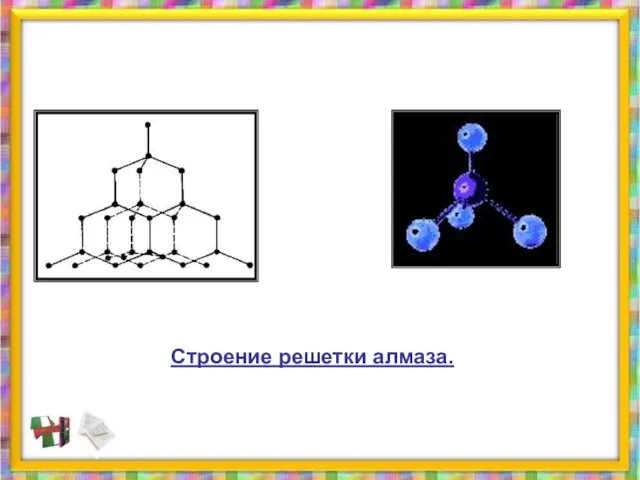
- 35. Строение решетки алмаза.
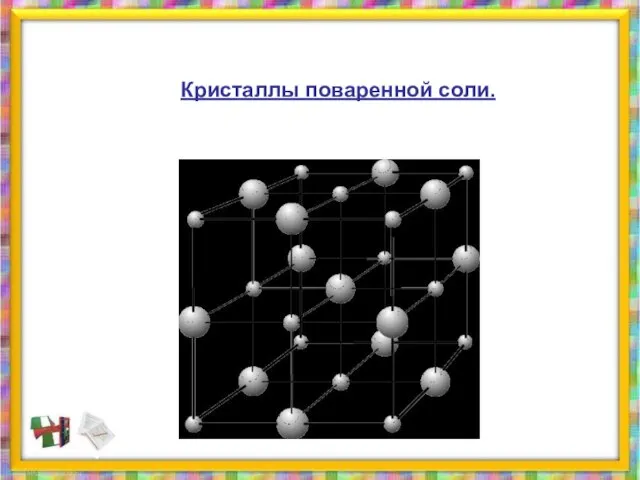
- 36. Кристаллы поваренной соли.
- 38. Биология
- 39. Вирус полиомиелита имеет форму додекаэдра.
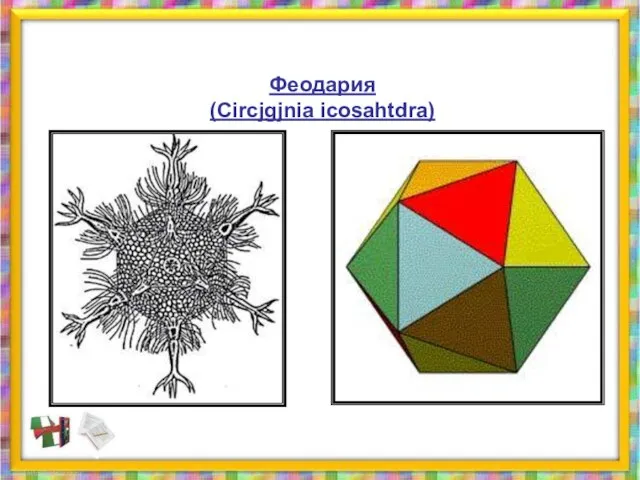
- 40. Феодария (Circjgjnia icosahtdra)
- 41. Искусство «Тайняя вечеря» С.Дали
- 42. ГРАВЮРА ГОЛАНДСКОГО ХУДОЖНИКА МАУРИЦА КОРНЕЛИУСА ЭШЕРА «СИЛЫ ГРАВИТАЦИИ»
- 44. Украшения
- 45. Правильная форма алмаза.
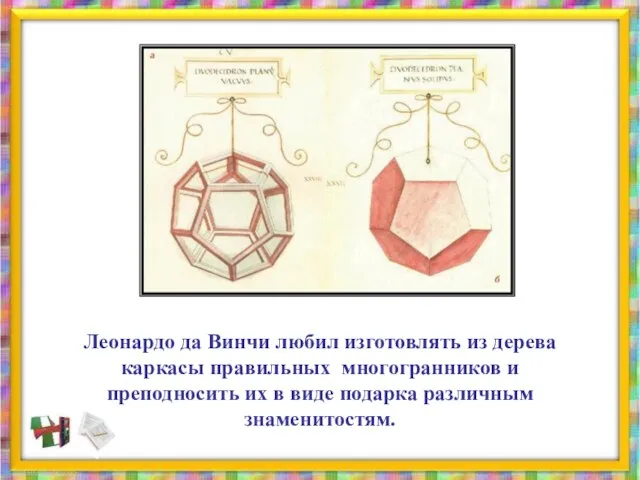
- 46. Леонардо да Винчи любил изготовлять из дерева каркасы правильных многогранников и преподносить их в виде подарка
- 48. Скачать презентацию
































 MadameTussaud’s Музей Восковых фигур Мадам Тюссо
MadameTussaud’s Музей Восковых фигур Мадам Тюссо Место учебного исследования в программе Intel «Обучение для будущего»
Место учебного исследования в программе Intel «Обучение для будущего» Потребительские кредиты
Потребительские кредиты Организация пастбищного содержания животных
Организация пастбищного содержания животных А
А Структура ВС РФ
Структура ВС РФ Северная Америка
Северная Америка «Как продолжается детство»
«Как продолжается детство» Молодые менеджеры и предприниматели Кубани
Молодые менеджеры и предприниматели Кубани Презентация на тему Углекислый газ СО2
Презентация на тему Углекислый газ СО2  Солнце воздух и вода – наши лучшие друзья
Солнце воздух и вода – наши лучшие друзья Лапта. История развития
Лапта. История развития Что такое система LanDrive ? LanDrive – это универсальная система управления по витой паре. Предназначена для автоматического и централиз
Что такое система LanDrive ? LanDrive – это универсальная система управления по витой паре. Предназначена для автоматического и централиз Презентация на тему Экологические кризисы и экологические катастрофы
Презентация на тему Экологические кризисы и экологические катастрофы История Громова Процессы на постсоветском пространстве
История Громова Процессы на постсоветском пространстве Шамшур
Шамшур Приобщение дошкольников к народной культуре в разных видах музыкальной деятельности»
Приобщение дошкольников к народной культуре в разных видах музыкальной деятельности» Тема урока
Тема урока Понятие о причастном обороте. Знаки препинания в предложениях с причастными оборотами. 6 класс
Понятие о причастном обороте. Знаки препинания в предложениях с причастными оборотами. 6 класс Презентация на тему Свет и его законы
Презентация на тему Свет и его законы  Презентация "Николай I и его портреты в изобразительном искусстве" - скачать презентации по МХК
Презентация "Николай I и его портреты в изобразительном искусстве" - скачать презентации по МХК Art City. Подбор квартиры
Art City. Подбор квартиры Фалсафа - 5
Фалсафа - 5 врол
врол Бабаево – взгляд с любовью (городской путеводитель)
Бабаево – взгляд с любовью (городской путеводитель) Бесприборные тесты для подтверждения ВИЧ-Инфекции
Бесприборные тесты для подтверждения ВИЧ-Инфекции Техника безопасностииорганизация рабочего места
Техника безопасностииорганизация рабочего места Конспект урока по окружающему миру (история)с использованием информационно-коммуникационных технологий (3 класс, программа 1-4).
Конспект урока по окружающему миру (история)с использованием информационно-коммуникационных технологий (3 класс, программа 1-4).