Презентация на тему: Моделирование расчетных системи отражение расчетов в балансе банков

Моделирование расчетных систем
Кафедра бухгалтерского учета и аудита экономического факультета РГУ
Под моделированием понимается изучение каких-либо объектов или процессов не прямо и непосредственно, а через специально созданные отражающие их изображения, образы или описания.
Цель моделирования — создание образа, адекватного его физическому оригиналу, то есть такого его описания, благодаря которому проявляются и становятся понятными его основные свойства.
Платежная система (payment system) состоит из ряда инструментов, банковских процедур и, как правило, межбанковских систем денежных переводов, которые обеспечивают денежное обращение.
Расчетная система (settlement system) — система, используемая для осуществления расчетов по сделкам (т. е. для перевода финансовых инструментов и(или) перечисления денежных средств).
Главной целью работы является представление экономических отношений, возникающих при осуществлении расчетов и платежей, методами математического моделирования.

Расчетные системы
Расчет на валовой основе (gross settlement) предполагает, что в соответствии с каждым поручением или требованием проводится отдельная операция посредством соответствующего перечисления средств. Платежи исполняются последовательно по мере их поступления и в соответствии с установленной очередностью обработки.
Нетто-расчет (net settlement) — расчет на основе чистой позиции взаимных требований и обязательств, его также называют клиринговым, или неттингом. Неттинг представляет собой расчет нетто-позиций по встречным платежам согласно суммам, отраженным в расчетных документах двух и более участников расчетов на нетто-основе, в соответствии с порядком проведения расчетов.

Расчетные системы
Системы брутто-расчетов различаются по скорости и порядку проведения расчетов. Расчеты на валовой основе могут проводиться непрерывно в течение дня (real-time), а могут осуществляться в заранее определенный период времени (batch).
Это определяет деление брутто-расчетных систем на расчеты в режиме реального времени и расчеты с периодической обработкой платежей.
Системы нетто-расчетов различаются по способу расчета нетто-позиции требований и обязательств — двухсторонний (bilateral) неттинг и многосторонний (multilateral) неттинг.

Матричные модели расчетов
Определим такие понятия, как матрица–корреспонденция и матрица–расчет (проводка)
Квадратная матрица размером m × m, у которой на пересечении строки, соответствующей участнику расчетов X, и столбца, соответствующему участнику Y, находится единица, а все остальные элементы равны нулю, называется матрицей-корреспонденцией.
Матрица-расчет — это произведение суммы расчетной операции на матрицу-корреспонденцию.
R (X, Y) = S X,Y · E(X,Y).

Матричная формула
валовых расчетов в режиме реального времени
где коэффициентами линейного разложения являются скалярные величины — суммы расчетных операций Si (i = 1, 2, …, n).
Представленная матричная формула — является информационно–технологическим образом журнала расчетных операций или системы валовых расчетов в режиме реального времени: в ней суммы операций, определенные на соответствующих корреспонденциях между участниками расчетов, представлены в хронологическом порядке.

Матричная формула валовых расчетов с периодической обработкой платежей
где коэффициентами линейного разложения будут суммы операций сводных проводок:
SX,Y (X, Y принадлежат множеству участников расчетов).
Представленная матричная формула — является информационно–технологическим образом расчетов за определенный период обработки или системы валовых расчетов с периодической обработкой платежей: в ней суммы операций — это итоговые суммы, определенные на однотипных корреспонденциях между участниками.

Матричная формула двухстороннего неттинга
Пусть R — это матрица обязательств по расчетам, R′ = (R)′ — транспонированная к ней матрица получаемых платежей или матрица исполнения обязательств,
то есть матрица, в которой строки и столбцы переставлены (инвертированы) по отношению к исходной матрице R.
Тогда сальдовая матрица ΔR будет определена
как разность:
ΔR = R - R′
Представленная матричная формула — является информационно–технологическим образом двухстороннего неттинга.

Векторно - матричная формула
многостороннего неттинга
Свертывание матриц обязательств и платежей в итоговый столбец достигается умножением справа на единичный вектор e. Преобразование r = R⋅e сворачивает R в итоговый столбец rоб (вектор обязательств), а преобразование r′ = R′⋅e в итоговый столбец rпл (вектор платежей).
Δrмн = ΔR⋅e.
Представленная векторно-матричная формула — является является информационно–технологическим образом многостороннего неттинга.

Матричные преобразования расчетных систем
Матричные преобразования, которые соответствуют переходам от одной системы расчетов к другой, можно определить следующим образом:
1) переход от системы валовых расчетов в режиме реального времени к системе валовых расчетов с периодической обработкой платежей осуществляется путем «приведения подобных» (суммированием) матриц расчетных операций за время периода обработки;
2) для перехода от системы валовых расчетов с периодической обработкой платежей к системе двухстороннего неттинга требуется из матрицы обязательств между участниками расчетов вычесть транспонированную к ней матрицу получаемых участниками платежей;
3) для перехода от системы двухстороннего неттинга к системе многостороннего неттинга необходимо сальдовую матрицу двухстороннего неттинга умножить на единичный вектор, результатом умножения являются многосторонние нетто-позиции каждого участника расчетов.

Иллюстрация матричных моделей и преобразований
в расчетных системах
Предположим, что по условиям задачи за период времени
t1 – t2 по данным двадцати трех расчетных документов, которыми обменивались пять участников расчетов (условно обозначаемых A, B, C, D, E), необходимо сформировать числовые выражения следующих моделей расчетных систем:
- валовых расчетов в режиме реального времени;
- валовых расчетов с периодической обработкой платежей;
- двухстороннего неттинга;
- многостороннего неттинга.

Иллюстрация матричных моделей и преобразований
в расчетных системах
Запишем числовое выражение формулы валовых расчетов в режиме реального времени, где суммы, указанные в расчетных документах, умножены на соответствующие матрицы-корреспонденции и записаны в хронологическом порядке в течение периода обработки (t1 – t2). Числовое выражение формулы примет следующий вид:
Rt1-t2 = 40E(А,B) + 80E(А,C) + 50E(А,D) + 30E(А,Е) + 70E(B,A) + 50E(B,C) + 40E(B,D) + 100E(B,Е) + 110E(C,A) + 40E(C,B) + 90E(C,D) + 60E(C,E) + 100E(D,A) + 120E(А,B) + 70E(D,C) + 140E(D,E) + 130E(E,A) + 20E(E,B) + 170E(E,C) + 30E(E,D) + 90E(A,B) + 190E(D,C) + 80E(B,D).
Заметим, что в течение периода обработки участник расчетов A три раза переводит средства участнику B, а участники D и B дважды передают расчетные документы соответственно участникам C и D, в то время как участник расчетов D не осуществляет переводов на участника B.

Иллюстрация матричных моделей и преобразований
в расчетных системах
Следовательно, числовое выражение формулы валовых расчетов с периодической обработкой платежей, после приведения подобных матриц расчетных операций (проводок) матрица расчетов будет иметь следующий вид:
Rt1-t2 = 250E(А,B) + 80E(А,C) + 50E(А,D) + 30E(А,Е) + 70E(B,A) + 50E(B,C) + 120E(B,D) + 100E(B,Е) + 110E(C,A) + 40E(C,B) + 90E(C,D) + 60E(C,E) + 100E(D,A) + 0E(D,B) + 260E(D,C) + 140E(D,E) + 130E(E,A) + 20E(E,B) + 170E(E,C) + 30E(E,D),

Иллюстрация матричных моделей и преобразований
в расчетных системах
или в традиционном матричном представлении:
Rt1-t2 =

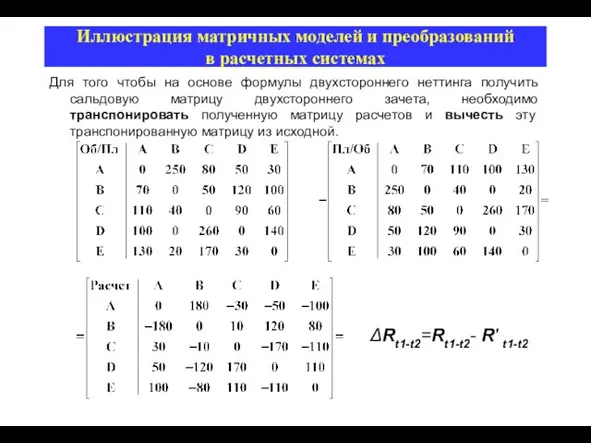
Иллюстрация матричных моделей и преобразований
в расчетных системах
Для того чтобы на основе формулы двухстороннего неттинга получить сальдовую матрицу двухстороннего зачета, необходимо транспонировать полученную матрицу расчетов и вычесть эту транспонированную матрицу из исходной.
ΔRt1-t2=Rt1-t2- R′ t1-t2

Иллюстрация матричных моделей и преобразований
в расчетных системах
На основе сальдовой матрицы двухстороннего неттинга, используя формулу многостороннего неттинга получаем числовое выражение вектора чистых позиций между участниками расчетов:
Δrt1-t2 =

Обзор задачи
Обзор приведенного примера показывает, что для осуществления расчетов валовым методом требуется значительно больше средств по сравнению с системами нетто-расчетов.
По данным нашей задачи видно, что, например, участнику расчетов А при проведении расчетов валовым способом требуются ликвидные средства в размере 410 единиц, а при проведении расчетов методом многостороннего неттинга он имеет нулевую нетто-позицию.
При осуществлении расчетов на основе двухстороннего неттинга между участниками A и B вместо 250 единиц расчетных активов участнику А требуется всего 180, а участник B вообще не затрачивает средств для осуществления двухсторонних расчетов.
Кроме этого, средства, необходимые для расчетов между всеми участниками при сравнении системы валовых расчетов и системы многостороннего неттинга расчетов, снижаются с 1900 (сумма обязательств всех участников) единиц расчетных активов до 260.

Обобщение
Рассмотрена система матричных образов и преобразований, которая позволяет методами математического моделирования проводить исследование расчетных систем. Отличительной особенностью этой системы являются компактность представления исходных данных и результатов расчетных операций, а также неалгоритмический способ преобразований расчетных систем.
Математический способ представления расчетных взаимоотношений позволяет сформировать единообразное понимание расчетных операций, которое не зависит от социальных, правовых и исторических традиций.
Изменения, происходящие в процессе развития платежных систем, являются полезными и эффективными только тогда, когда они однозначно интерпретируются людьми, которые практически реализуют принципы и концепции.

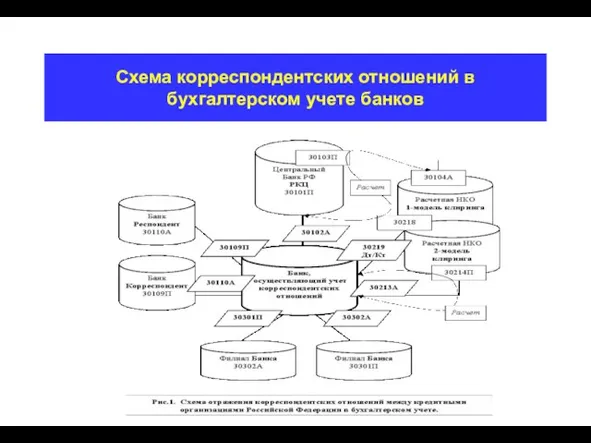
Схема корреспондентских отношений в бухгалтерском учете банков

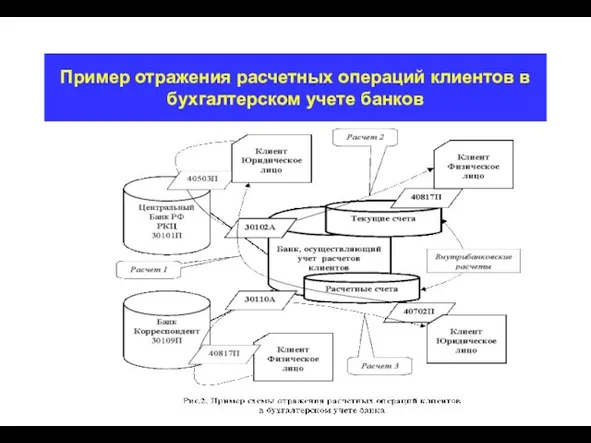
Пример отражения расчетных операций клиентов в бухгалтерском учете банков

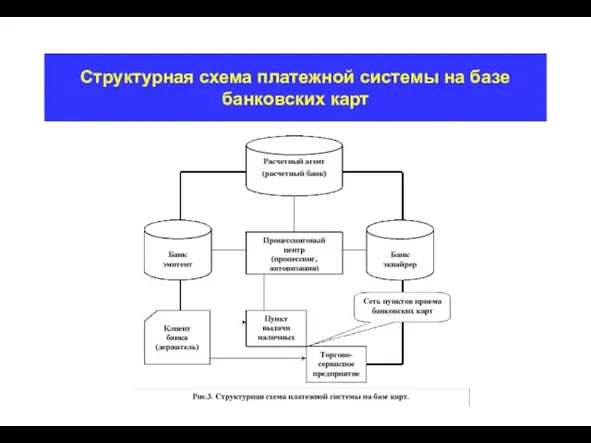
Структурная схема платежной системы на базе банковских карт

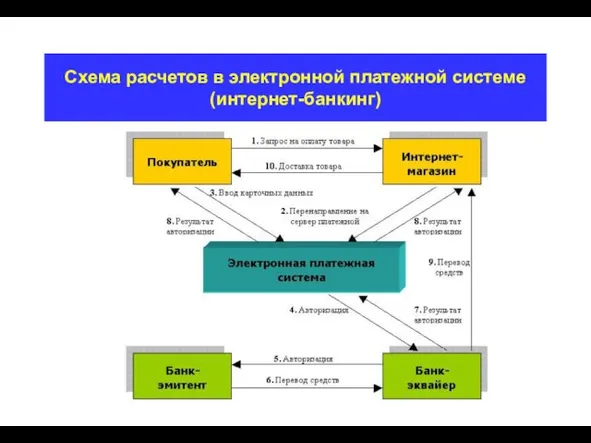
Схема расчетов в электронной платежной системе (интернет-банкинг)