Содержание
- 2. Задача о вычислении площади плоской фигуры Решим задачу о вычислении площади фигуры, ограниченной графиком функции ,
- 3. Задача о вычислении площади плоской фигуры
- 4. Задача о вычислении площади плоской фигуры
- 5. Определенный интеграл
- 6. Определенный интеграл
- 7. Определенный интеграл
- 8. Теорема о существовании определенного интеграла
- 9. Свойства определенного интеграла
- 10. Свойства определенного интеграла
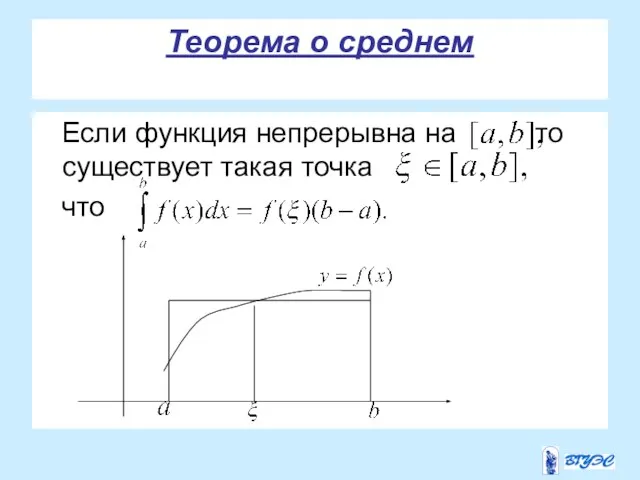
- 11. Теорема о среднем Если функция непрерывна на то существует такая точка что
- 12. Вычисление определенного интеграла
- 13. Пример Вычислить .
- 14. Вычисление интеграла
- 15. Пример
- 17. Пример
- 18. Несобственный интеграл
- 19. Пример . Вычислить несобственный интеграл (или установить его расходимость) . Этот несобственный интеграл расходится.
- 20. Пример Несобственный интеграл
- 21. Геометрические приложения определенного интеграла
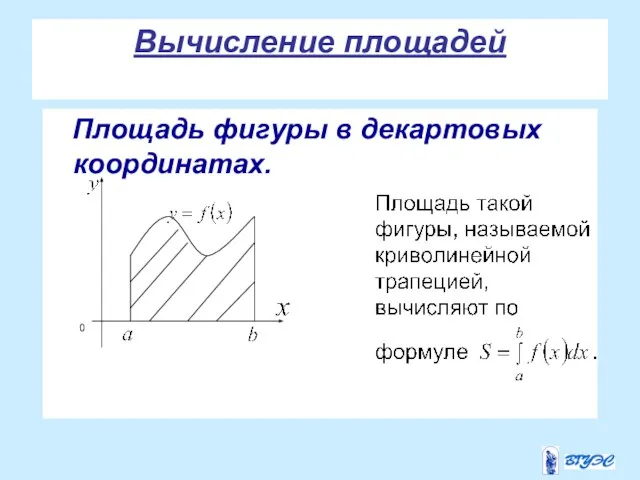
- 22. Вычисление площадей Площадь фигуры в декартовых координатах.
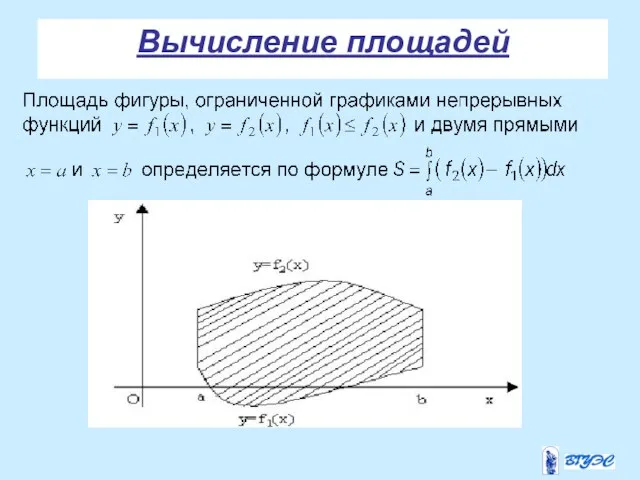
- 23. Вычисление площадей
- 24. Вычисление площадей В случае параметрического задания кривой, площадь фигуры, ограниченной прямыми , осью Ох и кривой
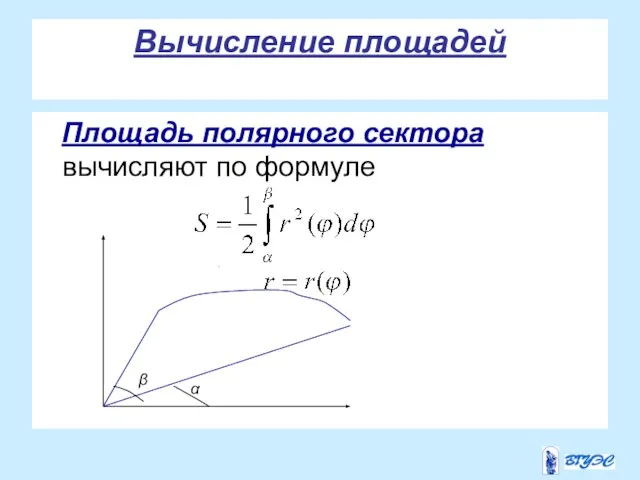
- 25. Вычисление площадей Площадь полярного сектора вычисляют по формуле . α β
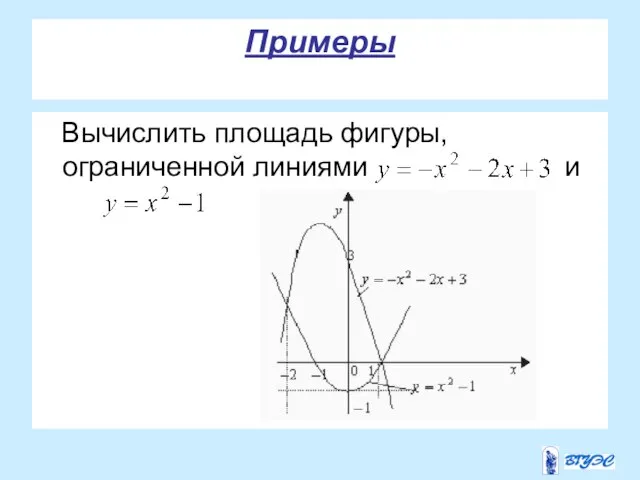
- 26. Примеры Вычислить площадь фигуры, ограниченной линиями и
- 27. Продолжение Получим
- 28. Примеры Найти площадь эллипса . Параметрические уравнения эллипса у о х
- 29. Пример Площадь фигуры, ограниченной лемнискатой Бернулли и лежащей вне круга радиуса :
- 30. Вычисление длины дуги Если кривая задана параметрическими уравнениями , , то длина ее дуги , где
- 31. Длина дуги в декартовых координатах Если кривая задана уравнением , то , где a, b–абсциссы начала
- 32. Длина дуги в полярных координатах Если кривая задана уравнением в полярных координатах , то , где
- 33. Примеры Вычислить длину дуги кривой от точки до . , тогда
- 34. Вычисление объема тела вращения. Объем тела, образованного вращением вокруг оси Ox криволинейной трапеции, ограниченной кривой ,
- 35. Вычисление объема тела вращения Объем тела, образованного вращением вокруг оси Oy фигуры, ограниченной кривой , отрезком
- 36. Вычисление объема тела вращения Искомый объем можно найти как разность объемов, полученных вращением вокруг оси Ox
- 38. Скачать презентацию






























 НазванияХимическихЭлементов
НазванияХимическихЭлементов Акты применения права. Характеристика и классификация
Акты применения права. Характеристика и классификация САМЫЕ-САМЫЕ
САМЫЕ-САМЫЕ Отчет о научно-организационной деятельности Президиума АН РБ в 2009 году
Отчет о научно-организационной деятельности Президиума АН РБ в 2009 году Невидимые нити (2 класс)
Невидимые нити (2 класс) НИКОЛАЯ ДМИТРИЕВИЧА ПАПАЛЕКСИ
НИКОЛАЯ ДМИТРИЕВИЧА ПАПАЛЕКСИ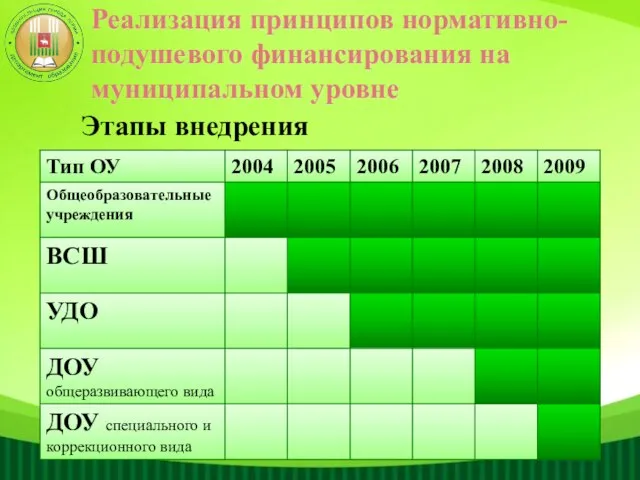 Реализация принципов нормативно-подушевого финансирования на муниципальном уровне
Реализация принципов нормативно-подушевого финансирования на муниципальном уровне Верейская по деньгам - ИТОГ
Верейская по деньгам - ИТОГ Дизайнер в отечественном ИТ бизнесе: многообразие деятельности, недооцененные компоненты профессионализма, стратегия роста Сер
Дизайнер в отечественном ИТ бизнесе: многообразие деятельности, недооцененные компоненты профессионализма, стратегия роста Сер Симметрия в архитектуре
Симметрия в архитектуре Презентация на тему Основные типы задач на проценты
Презентация на тему Основные типы задач на проценты  Вопросы внедрения национальной Интернет-адресации (IDN) .КАЗ
Вопросы внедрения национальной Интернет-адресации (IDN) .КАЗ Шаблон. Название темы
Шаблон. Название темы Презентация на тему Деревья
Презентация на тему Деревья  Учимся рисовать синичку (1)
Учимся рисовать синичку (1) Ох, уж эта функция
Ох, уж эта функция ЕДИНАЯ СИСТЕМА КЛАССИФИКАТОРОВ АНАЛИТИЧЕСКИХ ДАННЫХ
ЕДИНАЯ СИСТЕМА КЛАССИФИКАТОРОВ АНАЛИТИЧЕСКИХ ДАННЫХ Основы программирования промышленных роботов
Основы программирования промышленных роботов Образ матери в искусстве
Образ матери в искусстве Исследование опорно-двигательного аппарата учащихся Кугультинской средней школы
Исследование опорно-двигательного аппарата учащихся Кугультинской средней школы Шар ( сфера )
Шар ( сфера ) Школа нумерологии Светланы Сорокиной. Основы нумерологии. Базовый курс. Урок 2
Школа нумерологии Светланы Сорокиной. Основы нумерологии. Базовый курс. Урок 2 С Новым годом поздравляю
С Новым годом поздравляю Презентация на тему Книжная миниатюра Востока
Презентация на тему Книжная миниатюра Востока  О ДОЛГОСРОЧНОМ РЕГУЛИРОВАНИИ ТАРИФОВ НА УСЛУГИ ПО ПЕРЕДАЧЕ ТЕПЛОВОЙ ЭНЕРГИИ ООО «СВЕРДЛОВСКАЯ ТЕПЛОСНАБЖАЮЩАЯ КОМПАНИЯ»
О ДОЛГОСРОЧНОМ РЕГУЛИРОВАНИИ ТАРИФОВ НА УСЛУГИ ПО ПЕРЕДАЧЕ ТЕПЛОВОЙ ЭНЕРГИИ ООО «СВЕРДЛОВСКАЯ ТЕПЛОСНАБЖАЮЩАЯ КОМПАНИЯ» Начало Второй Мировой Войны
Начало Второй Мировой Войны Понятие психологии
Понятие психологии Страховые фонды Понятие, сущность, основные формы
Страховые фонды Понятие, сущность, основные формы