Презентация на тему Основные понятия и аксиомы стереометрии. Параллельность прямых и плоскостей

Начнём по порядку . что же такое стереометрия?
Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве.
Слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять.

Простейшие фигуры в пространстве: точка, прямая, плоскость.
Плоскость.
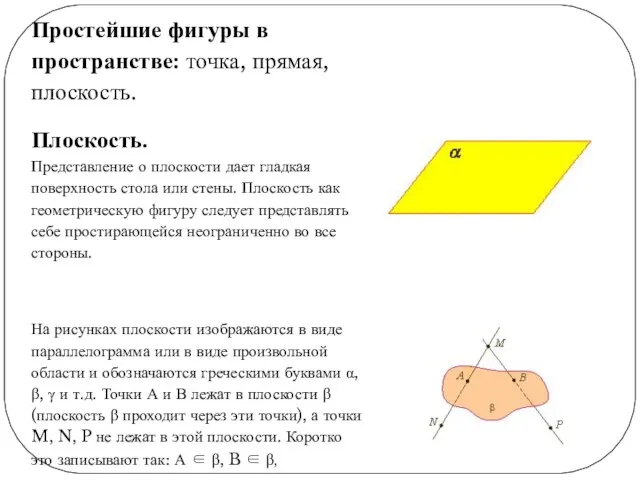
Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.
На рисунках плоскости изображаются в виде параллелограмма или в виде произвольной области и обозначаются греческими буквами α, β, γ и т.д. Точки А и В лежат в плоскости β (плоскость β проходит через эти точки), а точки M, N, P не лежат в этой плоскости. Коротко это записывают так: А ∈ β, B ∈ β,

Аксиомы стереометрии и их следствия , проверим себя . Аксиома 1
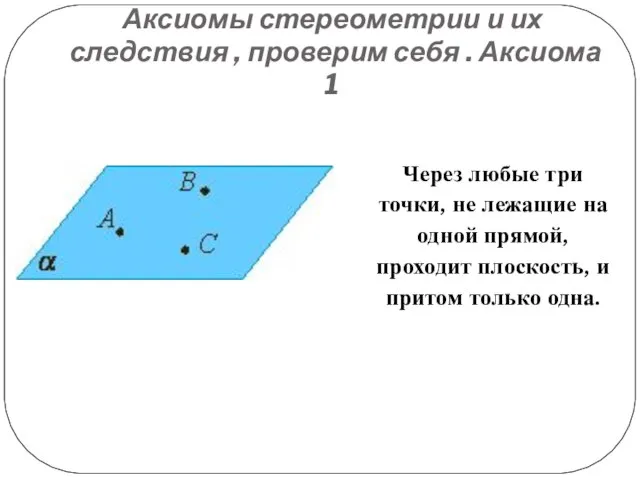
Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Аксиома 2
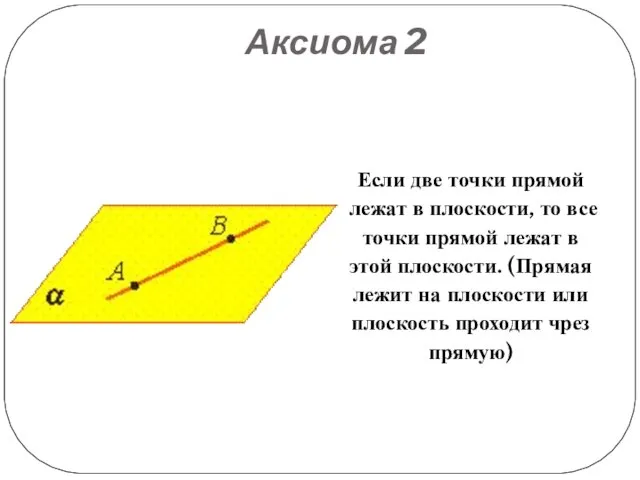
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. (Прямая лежит на плоскости или плоскость проходит чрез прямую)‏

Аксиома 3
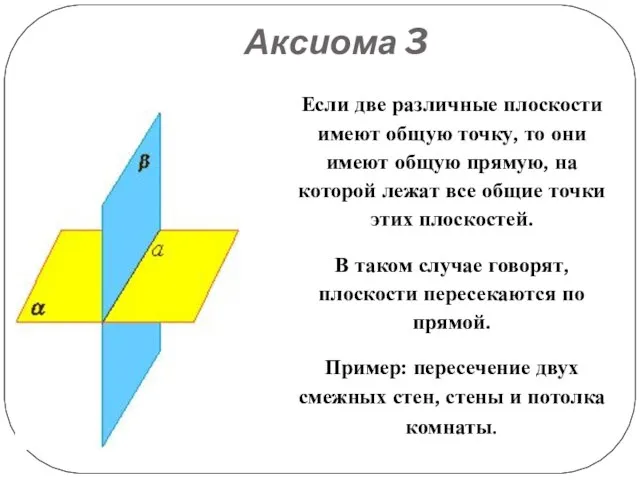
Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
В таком случае говорят, плоскости пересекаются по прямой.
Пример: пересечение двух смежных стен, стены и потолка комнаты.

Некоторые следствия из аксиом
Теорема 1.
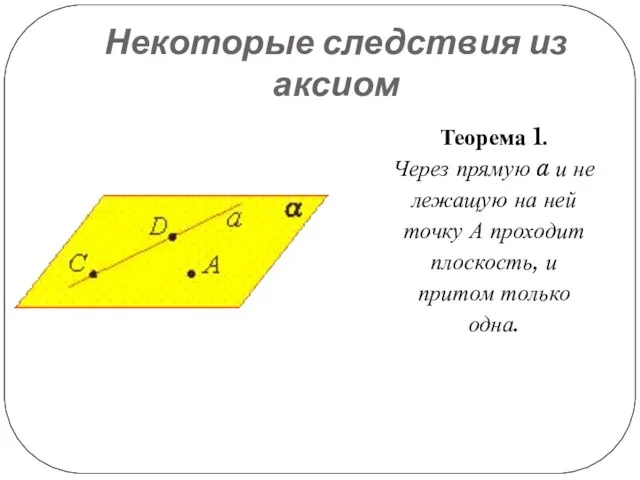
Через прямую a и не лежащую на ней точку А проходит плоскость, и притом только одна.

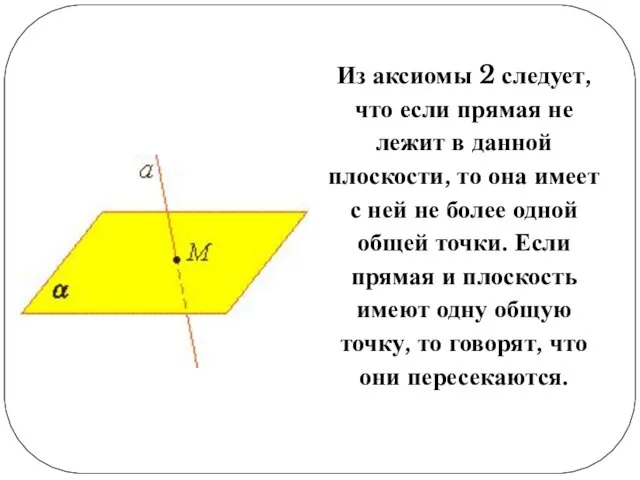
Из аксиомы 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются.

Теорема 3.
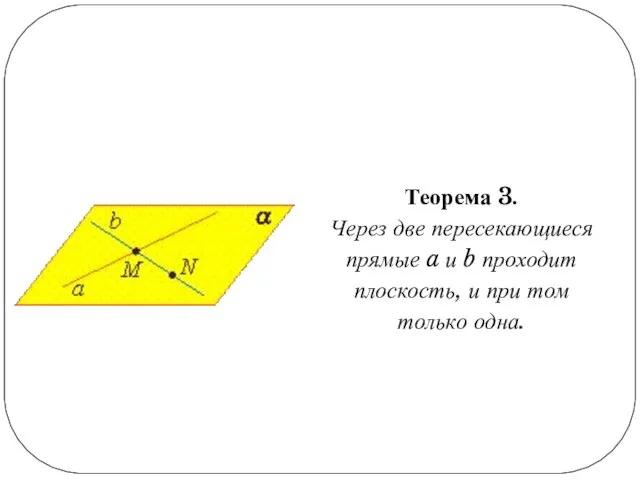
Через две пересекающиеся прямые a и b проходит плоскость, и при том только одна.

Параллельные прямые в пространстве .Введём понятие что называют параллельные прямые в пространстве
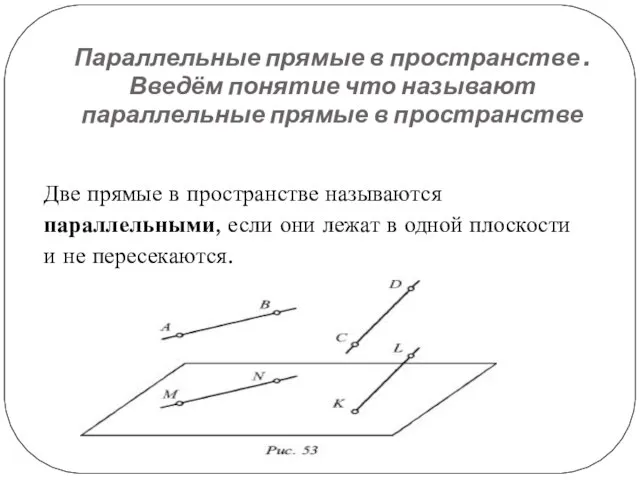
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Теорема о параллельных прямых.
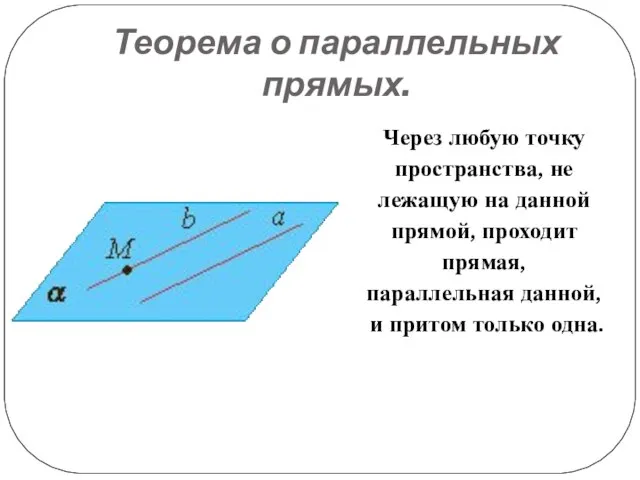
Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

Лемма о пересечении плоскости параллельными прямыми.
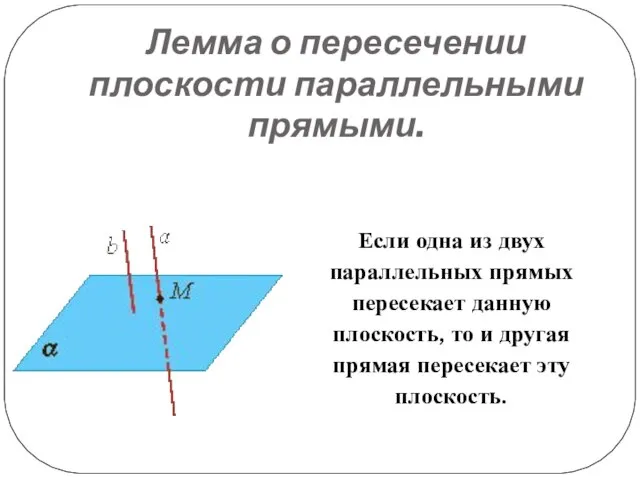
Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

Теорема о трех прямых в пространстве.
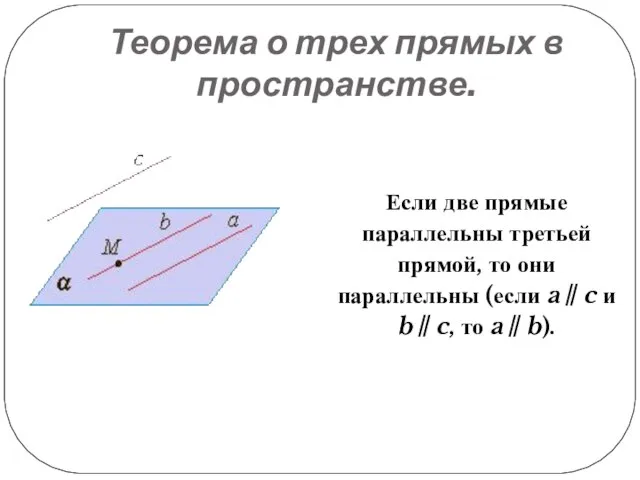
Если две прямые параллельны третьей прямой, то они параллельны (если a∥c и b∥c, то a∥b).