Слайд 2Решите уравнение:
4(х - 3) - 18 = 5(х - 5)
4х -

12 - 18 = 5х - 25
4х - 5х = 30 - 25
- х = 5
х = -5
Слайд 3Решите устно рациональным способом:
0,3 (-0,6) - (-0,7) (-0,6)
0
17
-0,6

Слайд 4Что общего в этих уравнениях?
Чем отличаются эти уравнения?

Слайд 5Разделите уравнения на группы.
По какому принципу можно разделить уравнения?

Слайд 6Повторим определение модуля.
Продолжите фразу:
Модулем положительного числа…
Модулем отрицательного числа…
Модулем нуля…

Слайд 7Заполните пропуски:
| ... | = 3
| ... | = 0
|
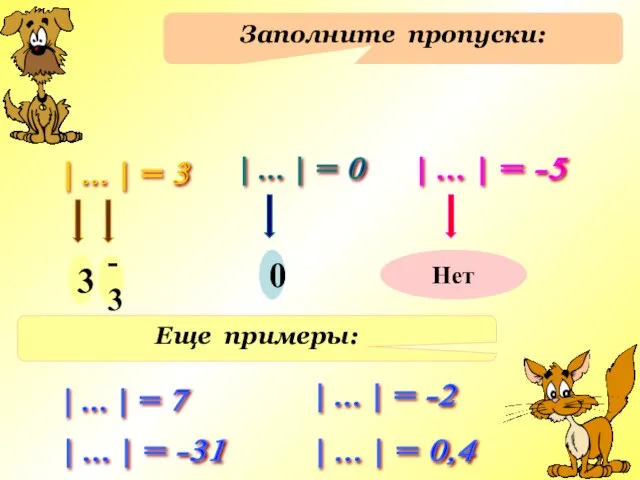
... | = -5
3
-3
0
Нет
Еще примеры:
| ... | = 7
| ... | = -2
| ... | = 0,4
| ... | = -31
Слайд 8Уравнения с переменной под знаком модуля решаются так:
I
| t | = a;

a > 0
t = a
t = -a
| x - 6 | = 3
Пример:
x - 6 = 3
x - 6 = -3
или
x = 9
x = 3
Ответ:
3; 9.
Слайд 9Решите уравнения:
| 2 + x | = 4
| 4 + x

| = 12
| 4x + 1 | = 3
| 2x - 4 | = 3
-6; 2
-16; 8
-1; 0,5
0,5; 3,5
Слайд 10Уравнения с переменной под знаком модуля решаются так:
II
| t | = 0

t = 0
| 2 + x | = 0
Пример:
2 + x = 0
x = -2
Ответ:
-2
Слайд 11Решите уравнения:
| 1 - 2x | = 0
| 7 + 2x

| = 0
| x + 4 | = 0
| 8x - 3 | = 0
0,5
-3,5
-4
0,375
Слайд 12Уравнения с переменной под знаком модуля решаются так:
III
| t | = a;

Нет корней
| 6 - x | = -5
Пример:
a < 0
Нет корней











 Курс Смешанная философия. Уральский гуманитарный институт
Курс Смешанная философия. Уральский гуманитарный институт Первая украинская горная экспедиция в Иран Сложные экспедиции в малодоступные уголки планеты
Первая украинская горная экспедиция в Иран Сложные экспедиции в малодоступные уголки планеты Новинки в ИКТ расширяют горизонты!
Новинки в ИКТ расширяют горизонты! История России 9 класс
История России 9 класс Петербург Достоевского
Петербург Достоевского жансултан презентация вена
жансултан презентация вена Презентация на тему Что мы знаем о своей стране и своём городе
Презентация на тему Что мы знаем о своей стране и своём городе Личностно-ориентированное консультирование (человеко/клиент-центрированный подход )
Личностно-ориентированное консультирование (человеко/клиент-центрированный подход ) Нарушение эмоций при поражении височных отделов мозга
Нарушение эмоций при поражении височных отделов мозга B1
B1 Проект благоустройства территории музея боевой техники под открытым небом
Проект благоустройства территории музея боевой техники под открытым небом ARKAN - Федеральный оператор безопасности
ARKAN - Федеральный оператор безопасности Презентация на тему город Чита
Презентация на тему город Чита  Плюрализм политической идеологии 19 века
Плюрализм политической идеологии 19 века Презентация на тему Царства Животные
Презентация на тему Царства Животные Искусственный свет. Искусственное освещение
Искусственный свет. Искусственное освещение «танграм» означает китайская головоломка
«танграм» означает китайская головоломка Сompetition
Сompetition Из истории Троице-Сергиева монастыря г. Великие Луки. Страницы жизни игумена Аркадия (Чанк)
Из истории Троице-Сергиева монастыря г. Великие Луки. Страницы жизни игумена Аркадия (Чанк) Рекомендации по исправлению визуализации продукции бренда Четвероногий гурман на сайте интернет-магазина Старая Ферма
Рекомендации по исправлению визуализации продукции бренда Четвероногий гурман на сайте интернет-магазина Старая Ферма 20141031_proektnaya_deyatelnost_na_urokakh_geografii_v_5_klasse_iz_opyta_raboty
20141031_proektnaya_deyatelnost_na_urokakh_geografii_v_5_klasse_iz_opyta_raboty Компания ДОМАСТЕР
Компания ДОМАСТЕР Проект для сотрудников (шаблон)
Проект для сотрудников (шаблон) Победа!
Победа! Отряд Куриные
Отряд Куриные Программа создания общероссийской сети центров публичного доступа к социально значимой информации (Программа ПЦПИ)
Программа создания общероссийской сети центров публичного доступа к социально значимой информации (Программа ПЦПИ) Формирование метапредметных компетенций школьников в урочной и внеурочной деятельности
Формирование метапредметных компетенций школьников в урочной и внеурочной деятельности ФИЗИКО-ХИМИЧЕСКИЕ ОСНОВЫ НАНОТЕХНОЛОГИИ
ФИЗИКО-ХИМИЧЕСКИЕ ОСНОВЫ НАНОТЕХНОЛОГИИ