Слайд 2Решите уравнение:
4(х - 3) - 18 = 5(х - 5)
4х -

12 - 18 = 5х - 25
4х - 5х = 30 - 25
- х = 5
х = -5
Слайд 3Решите устно рациональным способом:
0,3 (-0,6) - (-0,7) (-0,6)
0
17
-0,6

Слайд 4Что общего в этих уравнениях?
Чем отличаются эти уравнения?

Слайд 5Разделите уравнения на группы.
По какому принципу можно разделить уравнения?

Слайд 6Повторим определение модуля.
Продолжите фразу:
Модулем положительного числа…
Модулем отрицательного числа…
Модулем нуля…

Слайд 7Заполните пропуски:
| ... | = 3
| ... | = 0
|
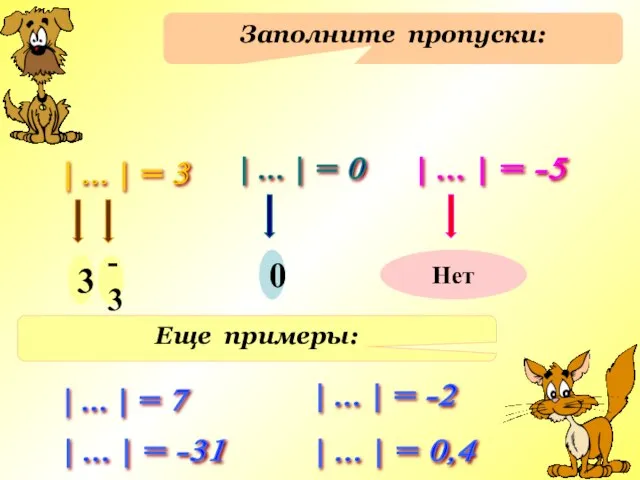
... | = -5
3
-3
0
Нет
Еще примеры:
| ... | = 7
| ... | = -2
| ... | = 0,4
| ... | = -31
Слайд 8Уравнения с переменной под знаком модуля решаются так:
I
| t | = a;

a > 0
t = a
t = -a
| x - 6 | = 3
Пример:
x - 6 = 3
x - 6 = -3
или
x = 9
x = 3
Ответ:
3; 9.
Слайд 9Решите уравнения:
| 2 + x | = 4
| 4 + x

| = 12
| 4x + 1 | = 3
| 2x - 4 | = 3
-6; 2
-16; 8
-1; 0,5
0,5; 3,5
Слайд 10Уравнения с переменной под знаком модуля решаются так:
II
| t | = 0

t = 0
| 2 + x | = 0
Пример:
2 + x = 0
x = -2
Ответ:
-2
Слайд 11Решите уравнения:
| 1 - 2x | = 0
| 7 + 2x

| = 0
| x + 4 | = 0
| 8x - 3 | = 0
0,5
-3,5
-4
0,375
Слайд 12Уравнения с переменной под знаком модуля решаются так:
III
| t | = a;

Нет корней
| 6 - x | = -5
Пример:
a < 0
Нет корней











 Презентация на тему Задачи на смеси и сплавы (9 класс)
Презентация на тему Задачи на смеси и сплавы (9 класс) Русская литература XX века: общая характеристика
Русская литература XX века: общая характеристика Денежные единицы мира
Денежные единицы мира Презентация на тему Золотой век Екатерины II
Презентация на тему Золотой век Екатерины II  Доходный подход к оценке
Доходный подход к оценке Музей Конфлуанс
Музей Конфлуанс Гендерные аспекты семейной политики Жанна Чернова НИУ-ВШЭ
Гендерные аспекты семейной политики Жанна Чернова НИУ-ВШЭ Презентация на тему Технология обработки древесины
Презентация на тему Технология обработки древесины Статистический анализ массовых наблюдений НЛО в восточном Оренбуржье
Статистический анализ массовых наблюдений НЛО в восточном Оренбуржье Поняття ЕТ Excel
Поняття ЕТ Excel Налоги: сущность и виды. Классификация
Налоги: сущность и виды. Классификация Внутреняя энергия
Внутреняя энергия В стране правовых знаний
В стране правовых знаний Убранство русской избы
Убранство русской избы Политико-правовая теория Монтескье
Политико-правовая теория Монтескье 169601
169601 Отделение восстановительного леченияреабилитация* неврологические больные (22,1%)* кардиологические больные (20,2%)* * травматол
Отделение восстановительного леченияреабилитация* неврологические больные (22,1%)* кардиологические больные (20,2%)* * травматол Франсуа Виет и его теорема (8 класс)
Франсуа Виет и его теорема (8 класс) Может ли природа жить без человека?
Может ли природа жить без человека? Юридическая ответственность и её виды
Юридическая ответственность и её виды Осенняя одежда
Осенняя одежда Банк внешней торговли (Внешторгбанк)
Банк внешней торговли (Внешторгбанк)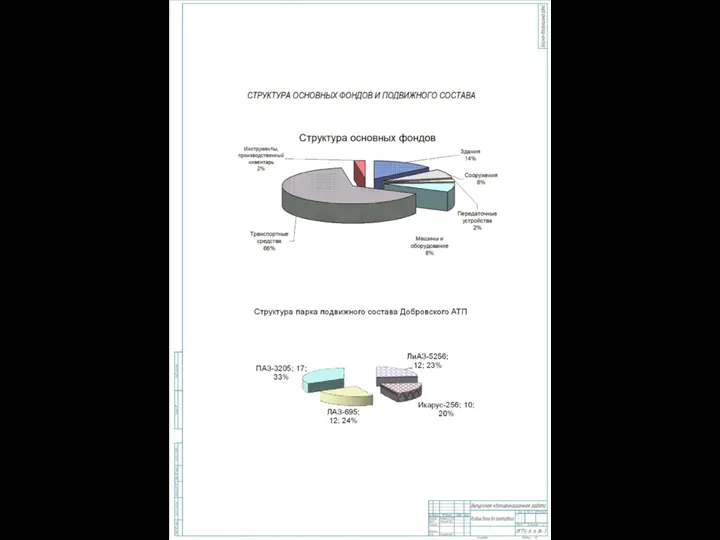 Структура основных фондов и подвижного состава
Структура основных фондов и подвижного состава Saint Isaac’s Square
Saint Isaac’s Square Агентство «Инсайт Маркетинг» решает задачи привлечения клиентов и повышения продаж при помощи инструментов интернет-маркетинга.
Агентство «Инсайт Маркетинг» решает задачи привлечения клиентов и повышения продаж при помощи инструментов интернет-маркетинга.  Педагогический совет
Педагогический совет Виды Смоленска
Виды Смоленска НАСС
НАСС