Презентация на тему Теорема о трех перпендикулярах

Цель урока:
Изучить теорему «О трех перпендикулярах».
Научиться применять её при решении задач.

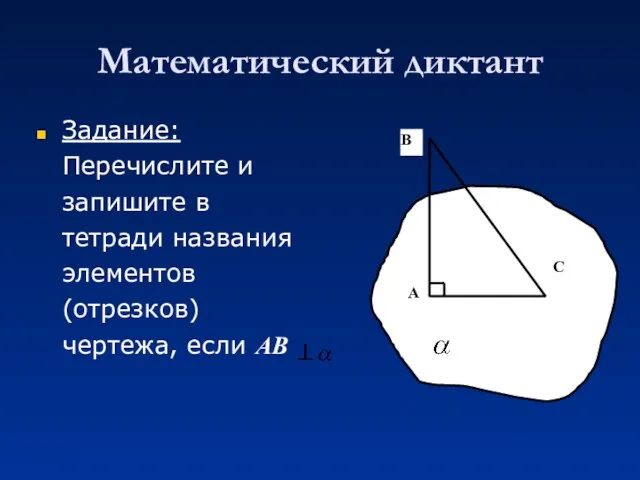
Математический диктант
Задание: Перечислите и запишите в тетради названия элементов (отрезков) чертежа, если АВ

Ответ:
АВ – перпендикуляр
ВС – наклонная
АС – проекция

Дополнительные вопросы:
Какой формулой связанны между собой перечисленные отрезки?
Чему равно ВС, если АВ = 3 см, АС = 4 см.?

Постановка проблемы
Через конец А отрезка АВ длины b, проведена плоскость, перпендикулярная отрезку. И в этой же плоскости проведена прямая с. Найти расстояние от точки В до прямой, если расстояние от точки А до прямой с равно а.

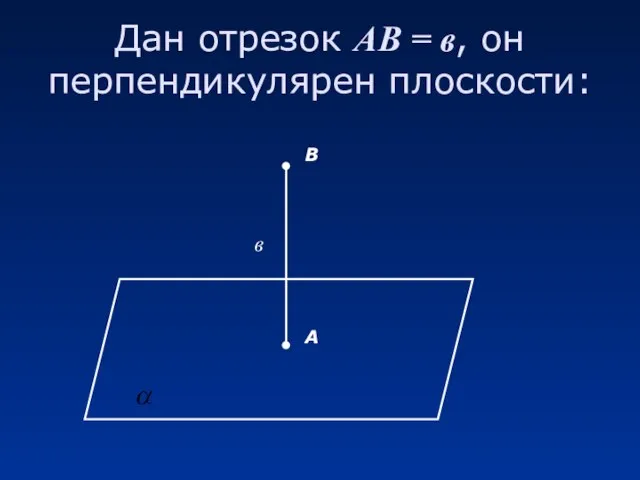
Дан отрезок АВ = в, он перпендикулярен плоскости:
А
В
в

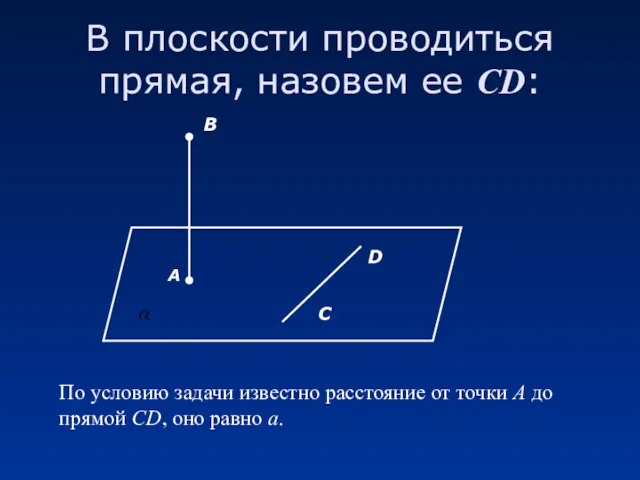
В плоскости проводиться прямая, назовем ее СD:
По условию задачи известно расстояние от точки А до прямой СD, оно равно а.

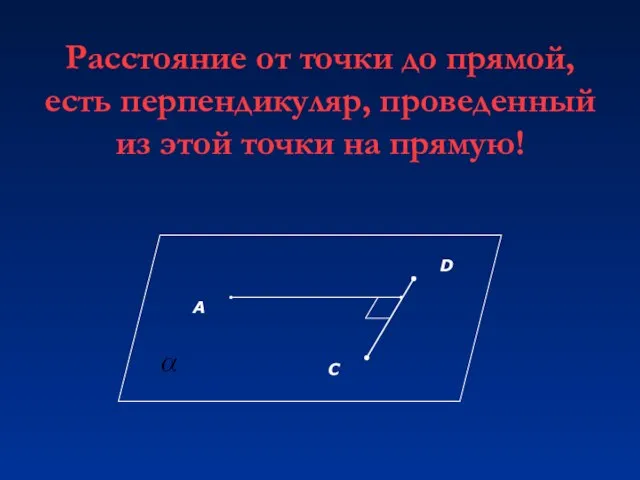
Расстояние от точки до прямой, есть перпендикуляр, проведенный из этой точки на прямую!

Теперь нужно выяснить, сколько перпендикуляров на чертеже и чему ровно АА1?
В
А
D
С
b
а
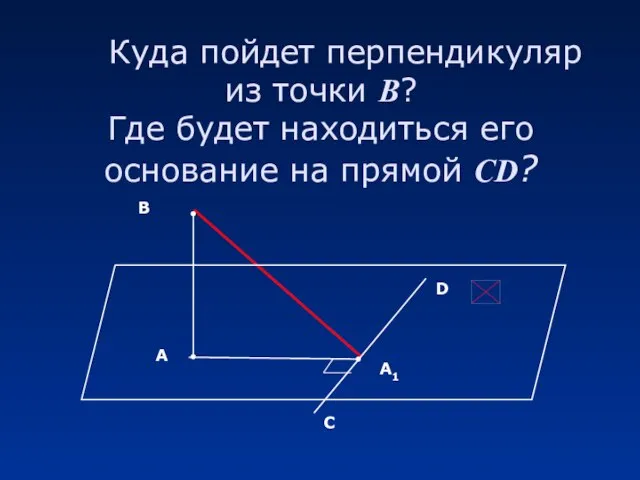
A1

Куда пойдет перпендикуляр из точки В?
Где будет находиться его основание на прямой CD?

Первый выступающий

Прямая, проведенная на плоскости через основание наклонной перпендикулярно ее проекции, перпендикулярна и самой наклонной.
А
В
А1
с
С
Дано: ; ,АС – наклонная,
ВС – проекция. ВС , АВ .
Доказать: АС

Второй выступающий

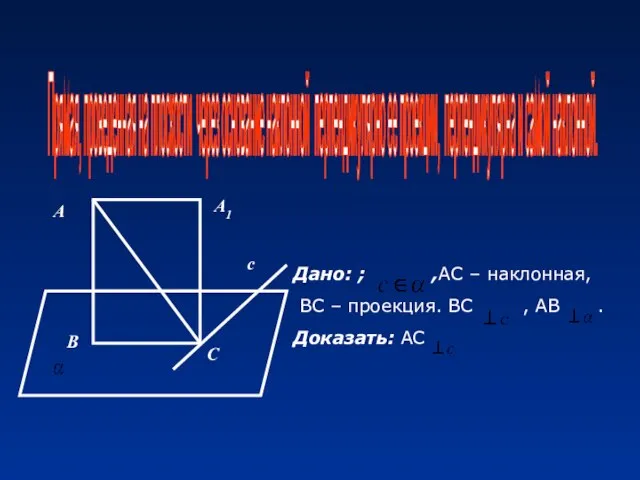
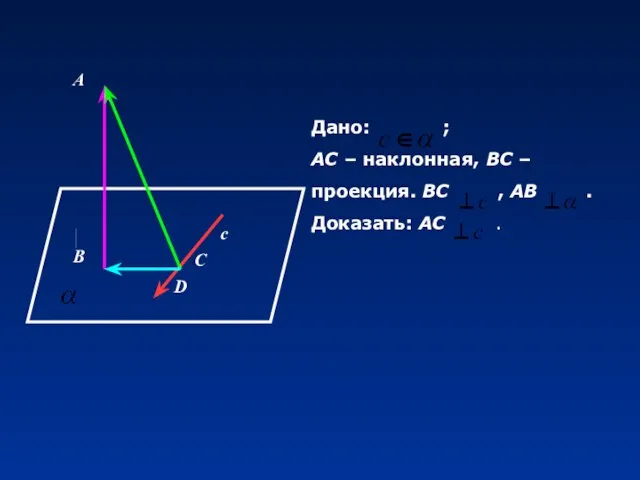
А
В
с
D
С
Дано: ;
АС – наклонная, ВС – проекция. ВС , АВ .
Доказать: АС .

Третий выступающий

*
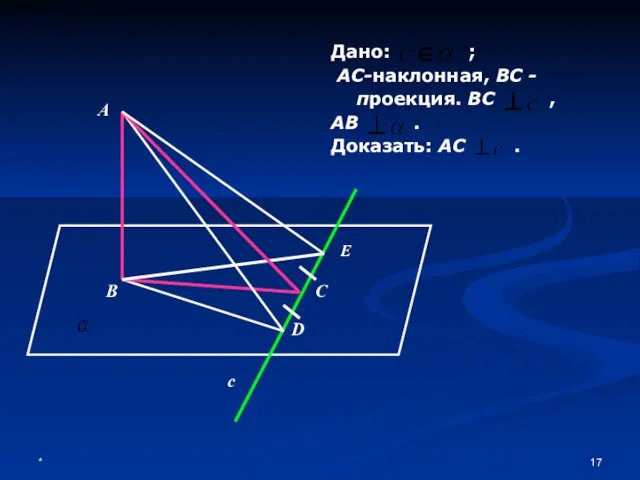
А
В
D
C
E
c
Дано: ;
АС-наклонная, ВС -проекция. ВС ,
АВ .
Доказать: АС .

Продолжим решение предложенной в начале урока задачи

*
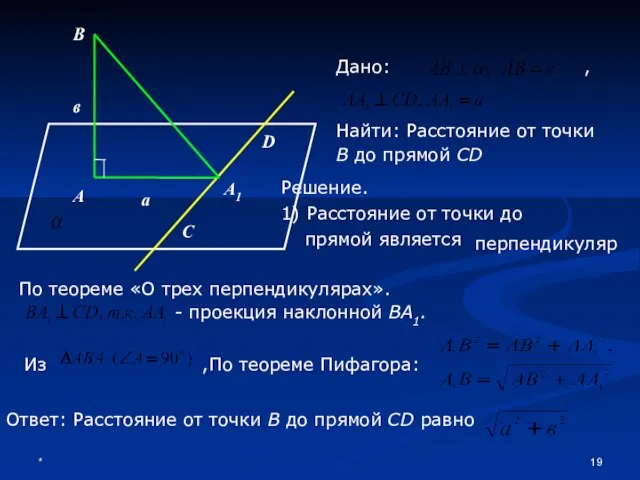
В
D
А
А1
в
а
С
Дано: ,
Найти: Расстояние от точки В до прямой CD
Решение.
1) Расстояние от точки до прямой является
перпендикуляр

Практическое применение теоремы о трех перпендикулярах

*
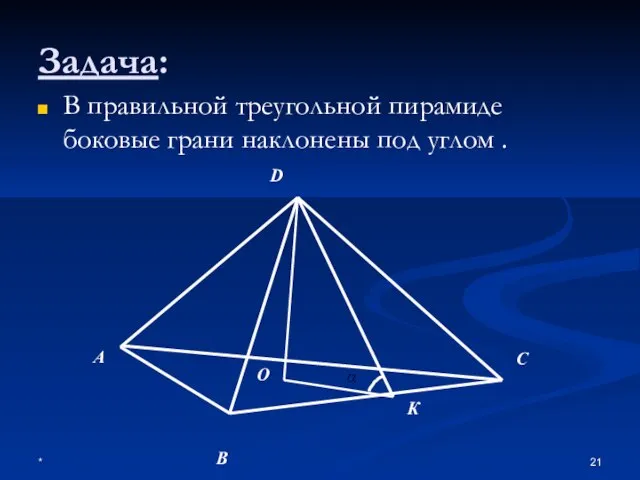
Задача:
В правильной треугольной пирамиде боковые грани наклонены под углом .
А
О
В
К
С
D

*
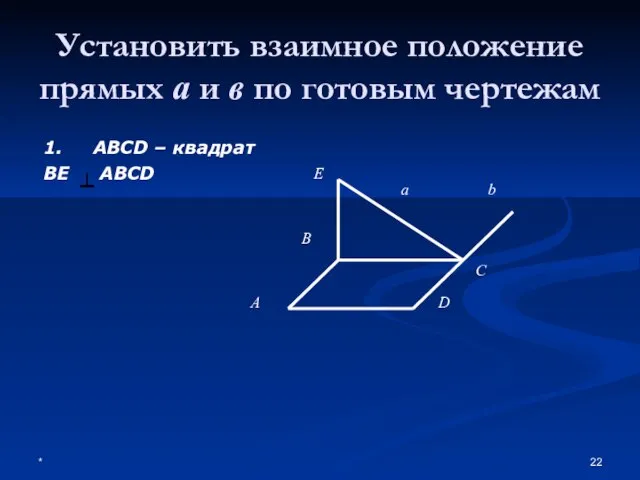
Установить взаимное положение прямых а и в по готовым чертежам
1. ABCD – квадрат
BE ABCD
A
b
a
C
B
D
E

*
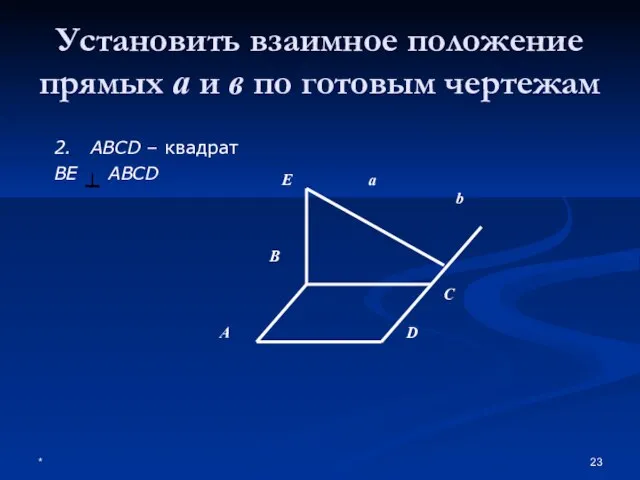
Установить взаимное положение прямых а и в по готовым чертежам
2. ABCD – квадрат
BE ABCD
A
b
a
C
B
D
E

*
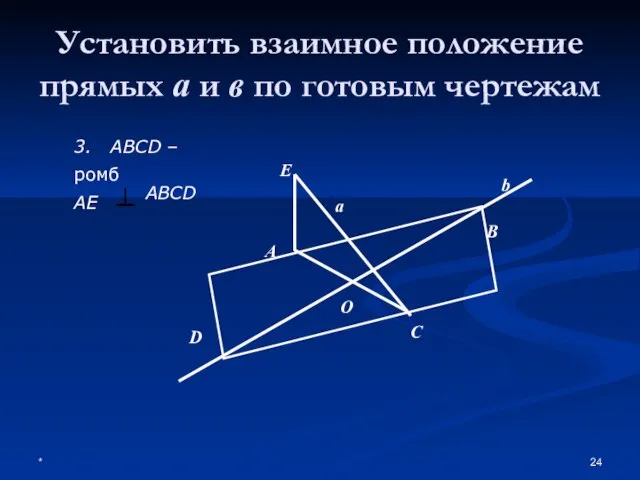
Установить взаимное положение прямых а и в по готовым чертежам
А
D
E
C
b
B
a
O

*
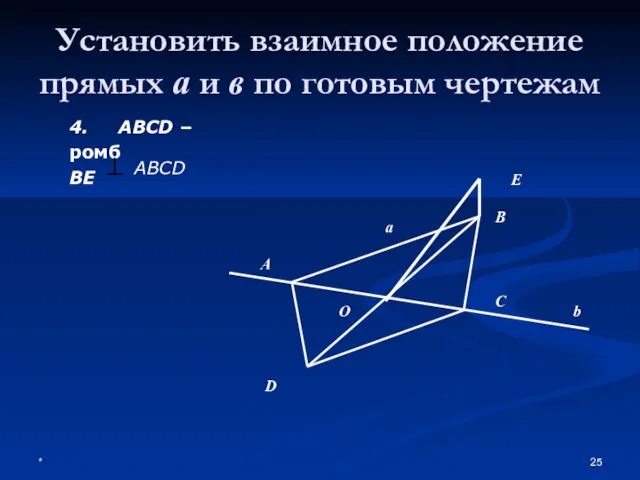
Установить взаимное положение прямых а и в по готовым чертежам
4. ABCD – ромб
BE
ABCD
А
D
E
C
b
B
a
O

*
Самостоятельная работа
На оценку 3: Решить 3 задачи из уровня А
На оценку 4: Решить по одной задачи из уровня А и В (на выбор любые).
На оценку 5: Решить по одной задачи из уровня А, В и С ( на выбор любые).