Содержание
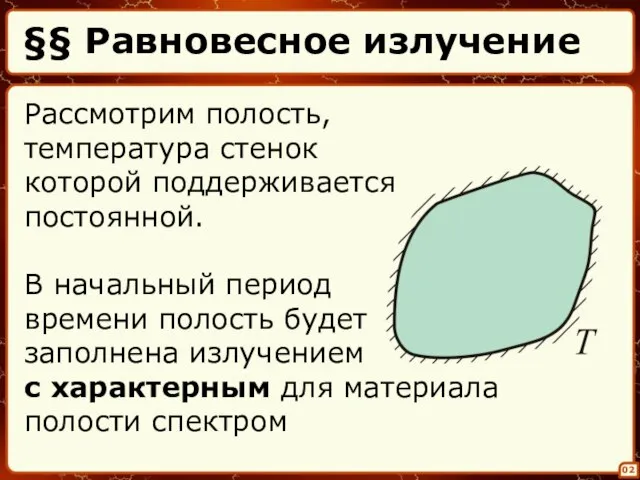
- 2. §§ Равновесное излучение 02 Рассмотрим полость, температура стенок которой поддерживается постоянной. В начальный период времени полость
- 3. 03 За счет частичного поглощения, за счет хаотического теплового движения, атомы полости переходят в возбужденное состояние
- 4. 04 Оно однородно, изотропно и деполяризовано. Спектральный состав и другие характе- ристики не зависят от свойств
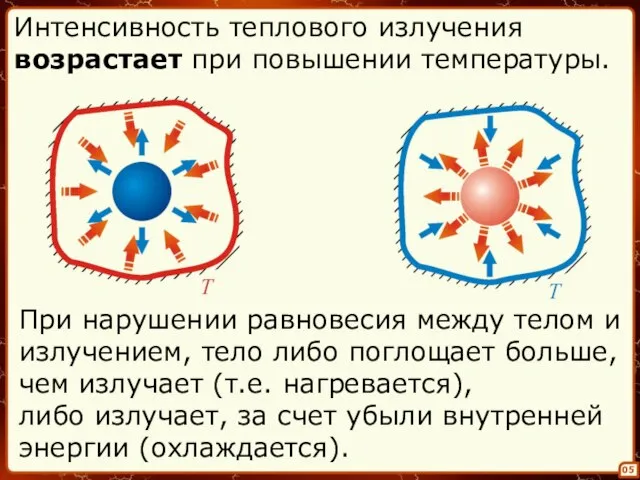
- 5. 05 При нарушении равновесия между телом и излучением, тело либо поглощает больше, чем излучает (т.е. нагревается),
- 6. §§ Характеристики излучения 06 Потоком (мощностью) излучения называется количество энергии, переносимой ЭМ волнами, за единицу времени
- 7. – распределение энергии по частотам (по длинам волн) 07 Энергетической светимостью называется величина, равная мощности теплового
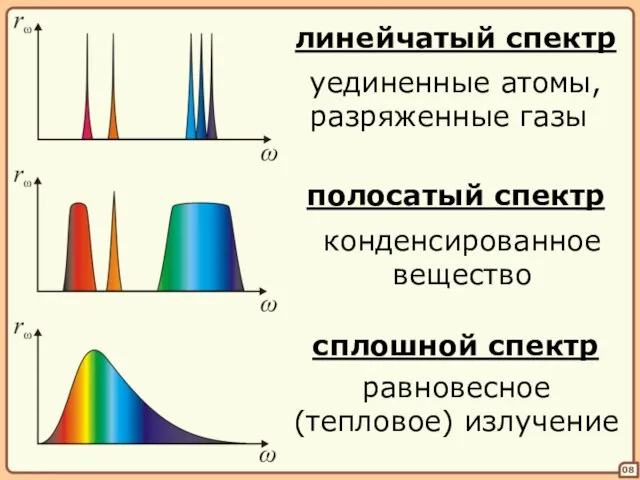
- 8. 08 линейчатый спектр уединенные атомы, разряженные газы полосатый спектр конденсированное вещество сплошной спектр равновесное (тепловое) излучение
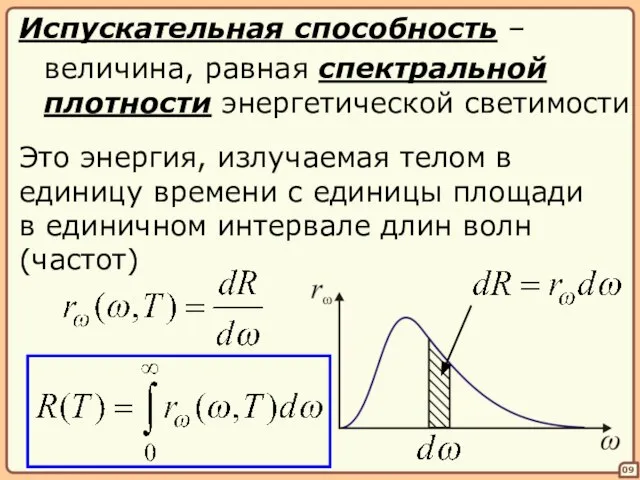
- 9. 09 Испускательная способность – величина, равная спектральной плотности энергетической светимости Это энергия, излучаемая телом в единицу
- 10. §§ Поглощательная способность 10 Рассмотрим элементарную площадку и интервал частот излучения [ω, ω + dω] Пусть
- 11. 11 Для абсолютно черного тела (АЧТ) Эта величина зависит от природы тела, частоты падающего излучения. температуры,
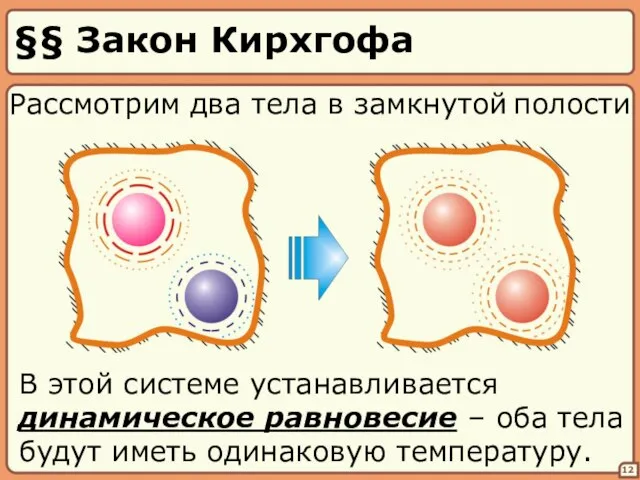
- 12. §§ Закон Кирхгофа 12 Рассмотрим два тела в замкнутой полости В этой системе устанавливается динамическое равновесие
- 13. – универсальная функция Кирхгофа 13 Если тело обладает большей излучательной способностью, то оно теряет на излучение
- 14. §§ Закон Стефана-Больцмана 14 Стефан, 1879, опытные данные – для любого тела Больцман, 1884, теоретический расчет
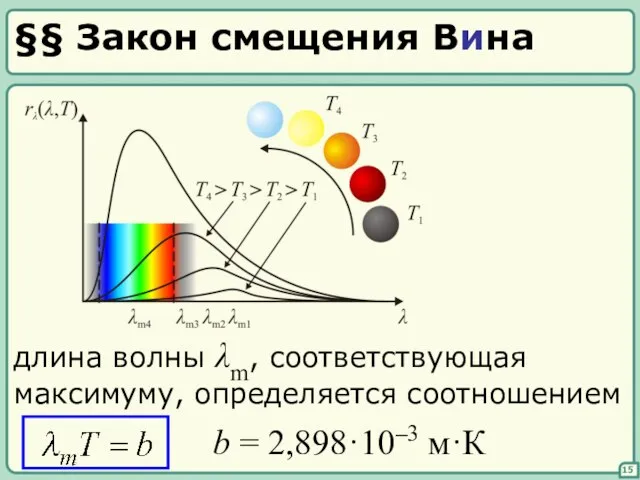
- 15. §§ Закон смещения Вина 15 длина волны λm, соответствующая максимуму, определяется соотношением b = 2,898·10–3 м·К
- 16. §§ Формула Рэлея–Джинса 16 Рассмотрим, следуя Рэлею (1900) и Джинсу (1905), вывод выражения для спектральной плотности
- 17. – энергия, приходящаяся на интервал частот [ω, ω + dω] 17 Энергия ЭМВ распределена по частотам
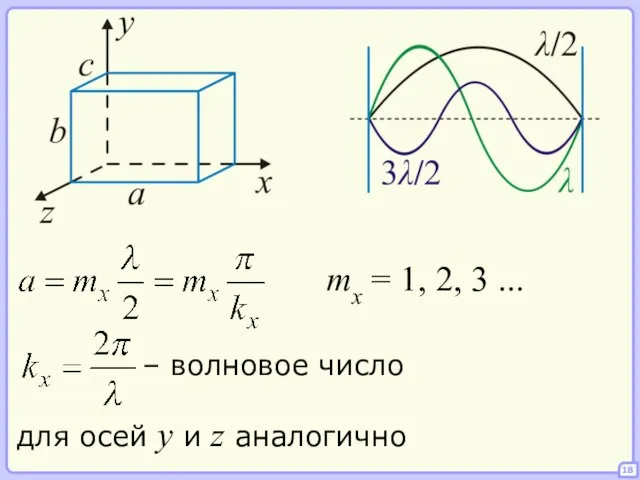
- 18. 18 mx = 1, 2, 3 ... для осей y и z аналогично
- 19. 19 – волновой вектор для встречных волн: Модуль волнового вектора:
- 20. 20 Вычислим приблизительное число таких волн N в зависимости от k. – объем, занимаемый всеми состояниями
- 21. 21 Число состояний следовательно, число волн в интервале [ω, ω + dω] равно Учтем независимость двух
- 22. 17 энергия, приходящаяся на интервал частот [ω, ω + dω] Из закона Больцмана следует, что на
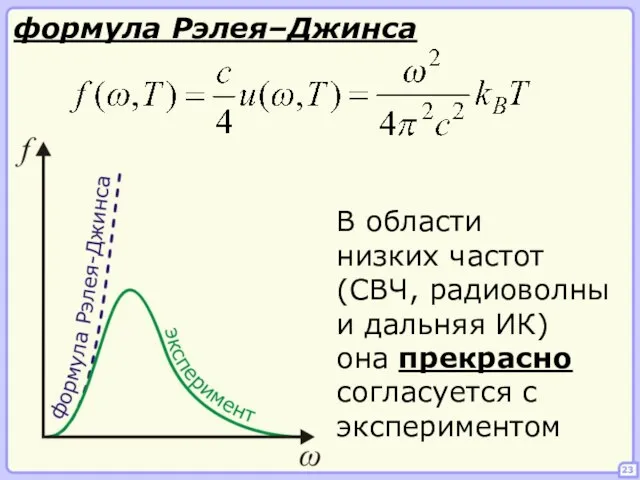
- 23. 23 формула Рэлея–Джинса В области низких частот (СВЧ, радиоволны и дальняя ИК) она прекрасно согласуется с
- 24. 24 Однако, и полученное выражение не описывает 1) равновесие между телом и излучением 2) уменьшение спектральной
- 25. §§ Формула Планка Спектральная плотность энергетической светимости (в данном случае – на одно колебание) 25
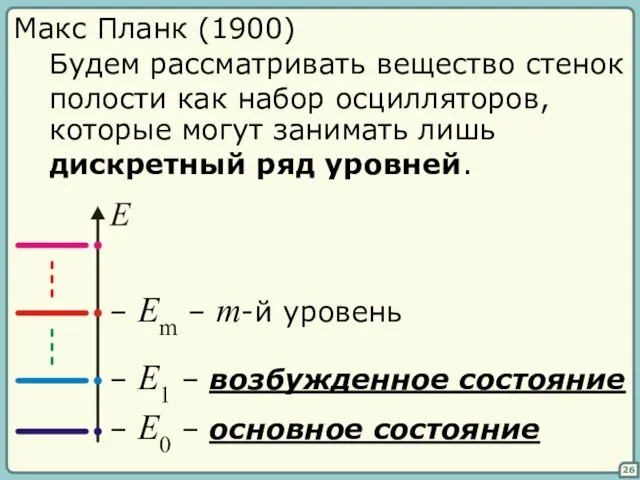
- 26. 26 Макс Планк (1900) Будем рассматривать вещество стенок полости как набор осцилляторов, которые могут занимать лишь
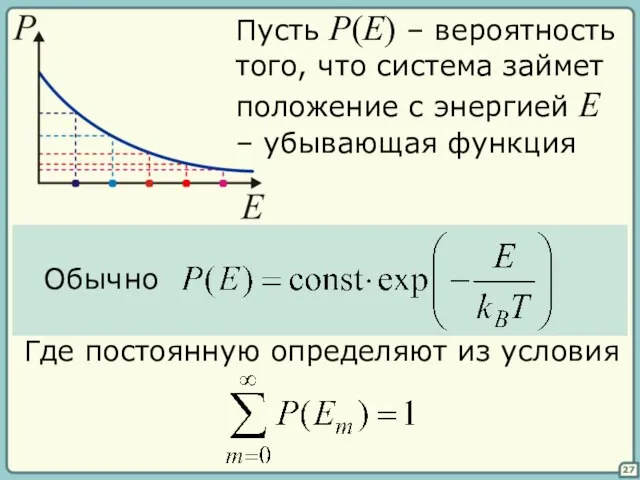
- 27. 27 Пусть P(E) – вероятность того, что система займет положение с энергией E – убывающая функция
- 28. 28 получаем или Средняя энергия:
- 29. 29 Пусть уровни – «равноотстоящие», т.е. тогда Вычислим сумму
- 30. 30 Следовательно
- 31. 31 классический предельный случай Планк предположил, что E0 ≠ 0 и определяется только свойствами излучения Пусть
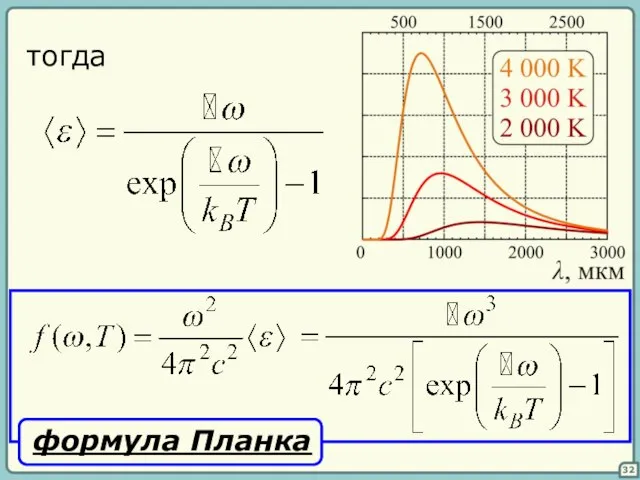
- 32. 32 тогда формула Планка
- 33. 33 Формула Планка дает исчерпывающее описание свойств теплового излучения. Она содержит: 1) закон Стефана–Больцмана 2) закон
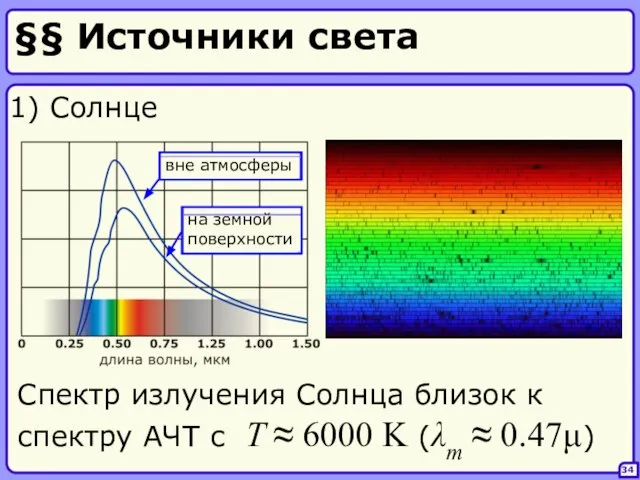
- 34. §§ Источники света 34 1) Солнце Спектр излучения Солнца близок к спектру АЧТ с T ≈
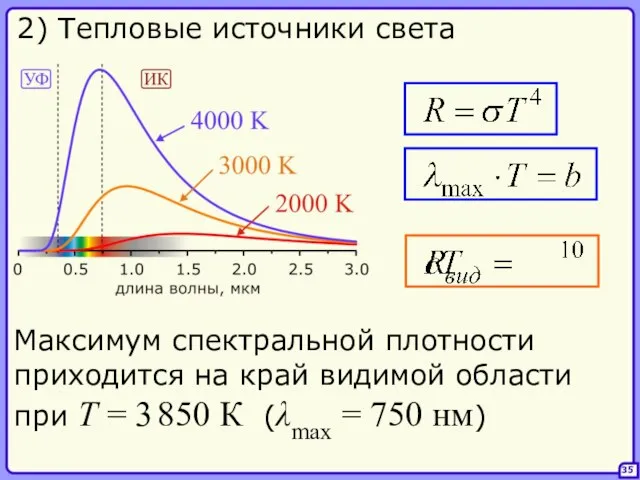
- 35. 35 2) Тепловые источники света Максимум спектральной плотности приходится на край видимой области при T =
- 36. 36 Дейви (Davy, 1778-1829) в начале 19 в. изобрел дуговую лампу Лодыгин, 1872 T ~ 2200
- 37. 37 1973 г., люминисцентные лампы Пары ртути в инертном газе (аргон, неон) испускают ультрафиолет, который вызывает
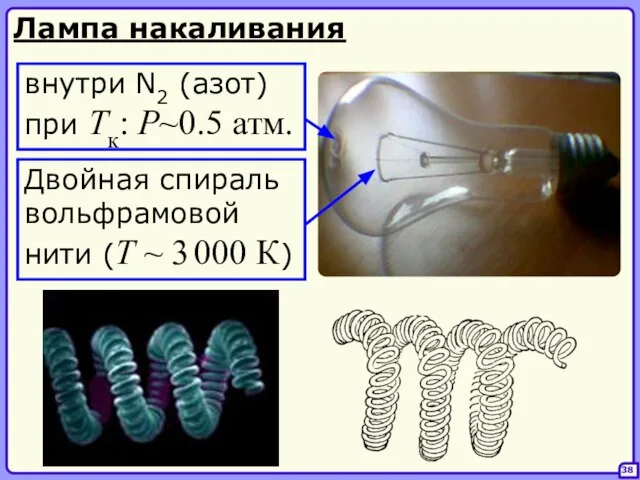
- 38. 38 Двойная спираль вольфрамовой нити (T ~ 3 000 К) внутри N2 (азот) при Tк: P~0.5
- 39. 39 Излучение вольфрама не соответствует излучению АЧТ, что приводит к большей светоотдаче. срок службы: 500-1500 ч.
- 40. – газоразрядные источники света 40 «Ксеноновые» лампы англ.: HID (High Intensity Discharge) источником света является электрическая
- 41. §§ Применение законов ТИ 1) ИК-сушка, нагрев 36 2) освещение (при T ~ 6700 K ηmax
- 43. Скачать презентацию









![– энергия, приходящаяся на интервал частот [ω, ω + dω] 17 Энергия](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/278859/slide-16.jpg)


![21 Число состояний следовательно, число волн в интервале [ω, ω + dω]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/278859/slide-20.jpg)
![17 энергия, приходящаяся на интервал частот [ω, ω + dω] Из закона](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/278859/slide-21.jpg)




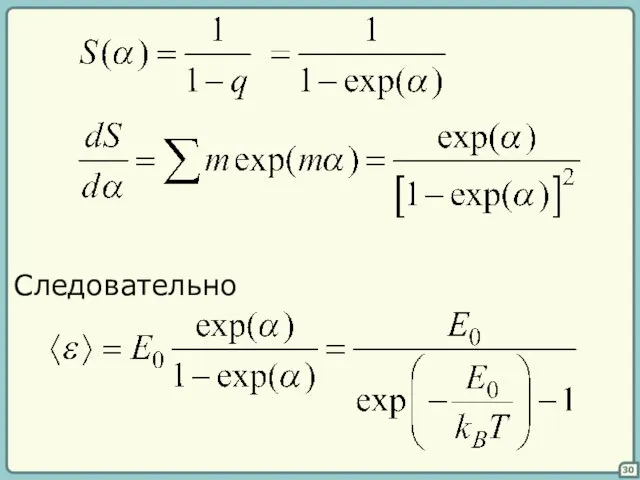







 Реализация проекта. План проекта мебель-трансформер
Реализация проекта. План проекта мебель-трансформер Урок презентация на тему Храм Василия Блаженного
Урок презентация на тему Храм Василия Блаженного  EISBERG MODELL
EISBERG MODELL «Преобразование транспортно-коммуникационных пространств городов. Санкт-Петербург. Площадь Балтийского вокзала»
«Преобразование транспортно-коммуникационных пространств городов. Санкт-Петербург. Площадь Балтийского вокзала» История одного города
История одного города Опыт использования учебников «Органическая химия» и «Общая химия» для обучения школьников на профильном уровне
Опыт использования учебников «Органическая химия» и «Общая химия» для обучения школьников на профильном уровне Презентация на тему Секреты долголетия
Презентация на тему Секреты долголетия Профсоюзы
Профсоюзы Налоговая реформа княгини Ольги
Налоговая реформа княгини Ольги Здоровьесберегающие образовательные технологии в педиатрии
Здоровьесберегающие образовательные технологии в педиатрии  Управление качеством образования на основе совершенствования научно-методической работы
Управление качеством образования на основе совершенствования научно-методической работы Практика стратегического анализа в российских городах
Практика стратегического анализа в российских городах МИСПИ(1)
МИСПИ(1) Анна Ахматова
Анна Ахматова Ребёнок один в машине
Ребёнок один в машине Китайские картины
Китайские картины Презентация на тему Требования к оформлению презентации
Презентация на тему Требования к оформлению презентации Требования к курсовой работе
Требования к курсовой работе Быстрая настройка рекламы в свадебной сфере!
Быстрая настройка рекламы в свадебной сфере! Калькулювання виробничой собівартості продукціи (робіт, послуг)
Калькулювання виробничой собівартості продукціи (робіт, послуг) СКОРО В ПРОДАЖЕ Артикул: 116012 Размер: 56,62 Лот 8 шт. Цвет: желтый, розовый, голубой, белый Полотно: капитон Примечания: застежка – кнопки
СКОРО В ПРОДАЖЕ Артикул: 116012 Размер: 56,62 Лот 8 шт. Цвет: желтый, розовый, голубой, белый Полотно: капитон Примечания: застежка – кнопки Street-Art et immeubles peints
Street-Art et immeubles peints Выбор ниши
Выбор ниши Презентация на тему Детство Пушкина (9 класс)
Презентация на тему Детство Пушкина (9 класс)  Полевые транзисторы. Самостоятельная работа
Полевые транзисторы. Самостоятельная работа Презентация на тему Жизнь и творчество А.Т. Твардовского
Презентация на тему Жизнь и творчество А.Т. Твардовского  Модерн в природе
Модерн в природе Закономерности эволюции
Закономерности эволюции