Содержание
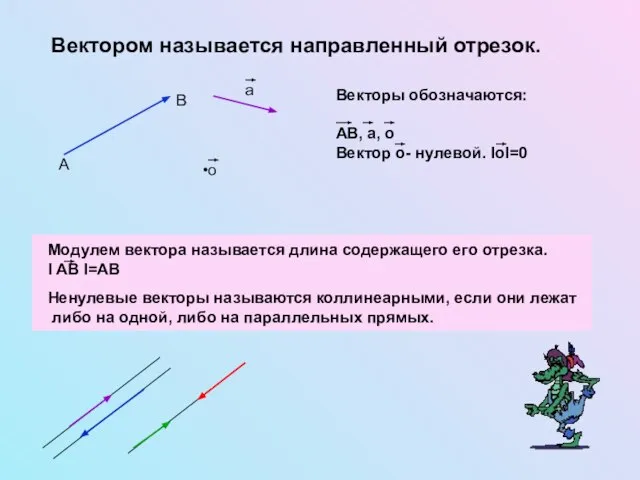
- 2. Вектором называется направленный отрезок. Модулем вектора называется длина содержащего его отрезка. l AB l=AB Ненулевые векторы
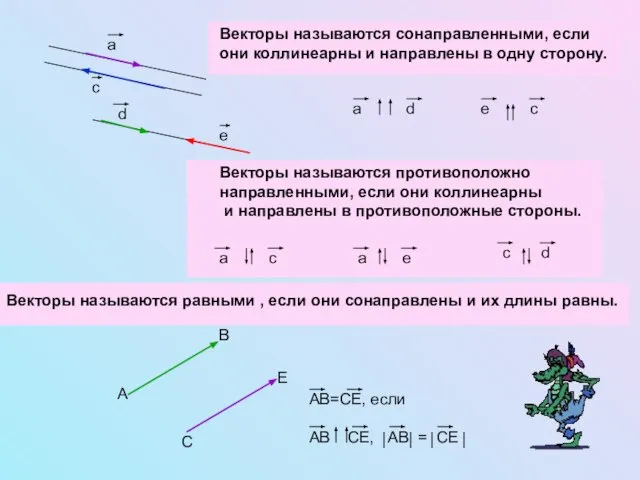
- 3. Векторы называются сонаправленными, если они коллинеарны и направлены в одну сторону. Векторы называются противоположно направленными, если
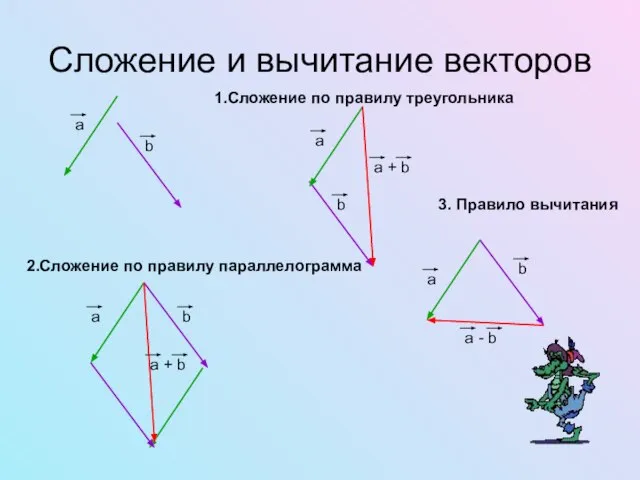
- 4. Сложение и вычитание векторов 1.Сложение по правилу треугольника 2.Сложение по правилу параллелограмма 3. Правило вычитания
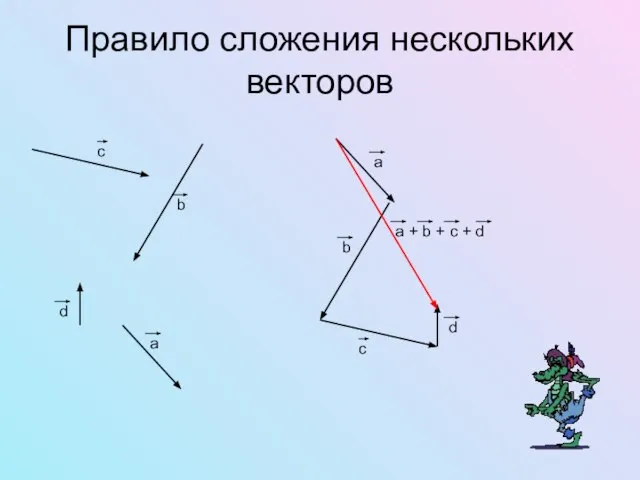
- 5. Правило сложения нескольких векторов
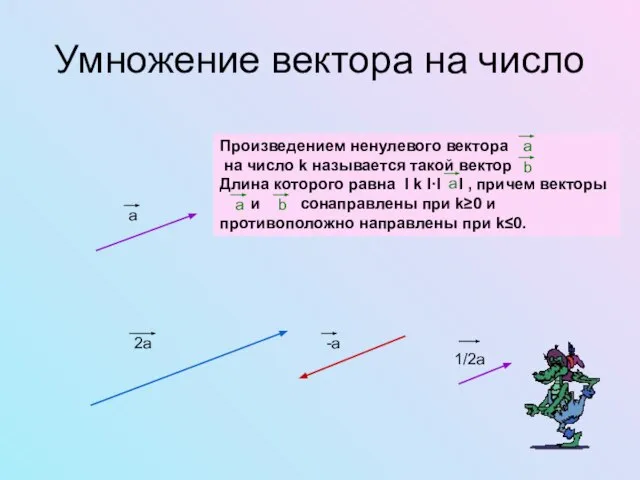
- 6. Умножение вектора на число Произведением ненулевого вектора на число k называется такой вектор Длина которого равна
- 7. Порешаем! Дано: ABCDA1B1C1D1 - параллелепипед. Упростите выражение: C1D-DA+CD+D1A1+AB1+CC1
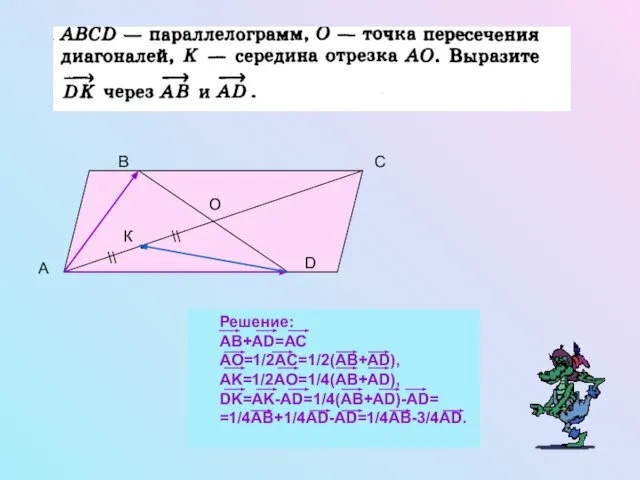
- 8. A B C D О К • \\ \\
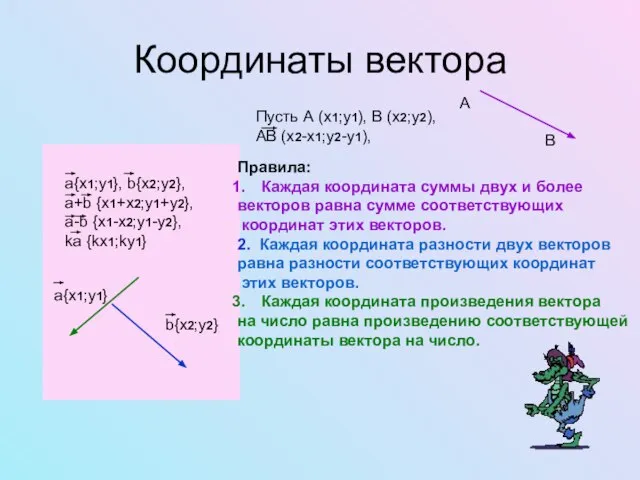
- 9. Координаты вектора А В Правила: Каждая координата суммы двух и более векторов равна сумме соответствующих координат
- 10. Порешаем! 1)Коллинеарны ли векторы а{4,8,12} и в{8,16,36}? Т.к. 8/4=2,16/8=2,36/12=3, то векторы не коллинеарны. 2)Найти координаты вектора
- 11. Формулы в координатах. • • 2.Расстояние между двумя точками А(х1;у1) В(х2;у2) 3.Вычисление длины вектора
- 12. Скалярное произведение векторов. Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
- 13. следствия Ненулевые векторы а{x1;y1} и b{x2;y2} перпендикулярны тогда и только тогда, когда их скалярное произведение равно
- 14. Порешаем! 1.Найдите площадь треугольника, вершины которого имеют координаты А(2;2),В(8;10),С(8;8) Ответ: 6
- 15. Порешаем! 2.Даны векторы а=mi+3j+4k и в=4i+mj-7k. При каком значении m векторы а и в перпендикулярны? Ответ:
- 16. Порешаем! 3.Дан треугольник АВС. А(-6;1)В(2;4)С(2;-2) Доказать:1)треугольник АВС равнобедренный 2)найти высоту треугольника, проведенную из вершины А Ответ:8
- 17. Порешаем! 4.При каком значении t вектор 2a+tb перпендикулярен вектору b-a, если a{2;-1}, b{4;3}? Ответ: 0
- 18. Порешаем! С А В 8 17 15 Ответ: а) 225,64,0 б)17П
- 21. Скачать презентацию











 Материаловедение
Материаловедение Презентация на тему Мода-2014
Презентация на тему Мода-2014 Жестокое обращение с детьми
Жестокое обращение с детьми Питание -
Питание - хаки
хаки Analyse de la zone d ’intervention du chef de groupe
Analyse de la zone d ’intervention du chef de groupe Кострома
Кострома Анализ положения тела при команде Внимание
Анализ положения тела при команде Внимание 1. Долиною плача и скорби иду я, Изранены ноги, нет силы идти; Хоть трудно, но все же шагаю, минуя Соблазны и бездны греха на пути.
1. Долиною плача и скорби иду я, Изранены ноги, нет силы идти; Хоть трудно, но все же шагаю, минуя Соблазны и бездны греха на пути. Историческая типология культуры (заключение)
Историческая типология культуры (заключение) Взрыв и взрывчатые вещества
Взрыв и взрывчатые вещества УНИВЕРСИТЕТСКАЯ БИБЛИОТЕКА В ИНФОРМАЦИОННО-ОБРАЗОВАТЕЛЬНОЙ СРЕДЕ Опарина О. Д., г. Екатеринбург, Уральский государственный униве
УНИВЕРСИТЕТСКАЯ БИБЛИОТЕКА В ИНФОРМАЦИОННО-ОБРАЗОВАТЕЛЬНОЙ СРЕДЕ Опарина О. Д., г. Екатеринбург, Уральский государственный униве Презентация на тему Александр Сергеевич Пушкин
Презентация на тему Александр Сергеевич Пушкин  Парные согласные звуки
Парные согласные звуки Art-terapy. Дудлинг. Зентангл
Art-terapy. Дудлинг. Зентангл Экскурсия в галерею искусств на Пушкинской. Тематическая выставка
Экскурсия в галерею искусств на Пушкинской. Тематическая выставка Достопримечательости д. Грузины
Достопримечательости д. Грузины Тема 5
Тема 5 Человек в религиозных традициях мира
Человек в религиозных традициях мира Система бухгалтерских счетов и двойная запись
Система бухгалтерских счетов и двойная запись Беседа – как метод работы с отдельными детьми
Беседа – как метод работы с отдельными детьми 20171215_ispolzovanie_vody_v_hozyaystve
20171215_ispolzovanie_vody_v_hozyaystve LEKTsIYa_LOGIChESKIE_OSNOVY_EVM
LEKTsIYa_LOGIChESKIE_OSNOVY_EVM Презентация на тему Спасская башня Московского Кремля (3 класс)
Презентация на тему Спасская башня Московского Кремля (3 класс) Питательные вещества и пищевые продукты
Питательные вещества и пищевые продукты Республика Саха-Якутия
Республика Саха-Якутия Что я знаю об этом ?
Что я знаю об этом ? Презентация на тему Осторожно, тонкий лед
Презентация на тему Осторожно, тонкий лед