Презентация на тему Задания с параметром ЕГЭ C5

№1. Найдите все значения a, при каждом из которых
система не имеет решений.
Решение: Рассмотрим второе неравенство системы
Произведение должно быть положительным.
Если а = 1, то неравенство, а значит и система не имеет решений. (0 > 8)
Если а < 1, то решение неравенства – луч
Если а > 1, то решение неравенства – луч

При а  1 первое неравенство системы
принимает вид:
Или при условии

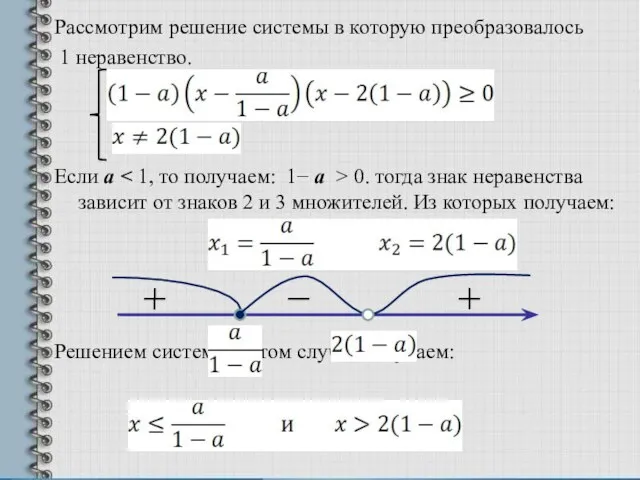
Рассмотрим решение системы в которую преобразовалось
1 неравенство.
Если а < 1, то получаем: 1 а > 0. тогда знак неравенства зависит от знаков 2 и 3 множителей. Из которых получаем:
Решением системы в этом случае получаем:

Если а > 1, то получаем: 1  а < 0, значит произведение 2 и 3 множителей должно быть отрицательным.
Решение в этом случае – полуинтервал :
Отметим, что .

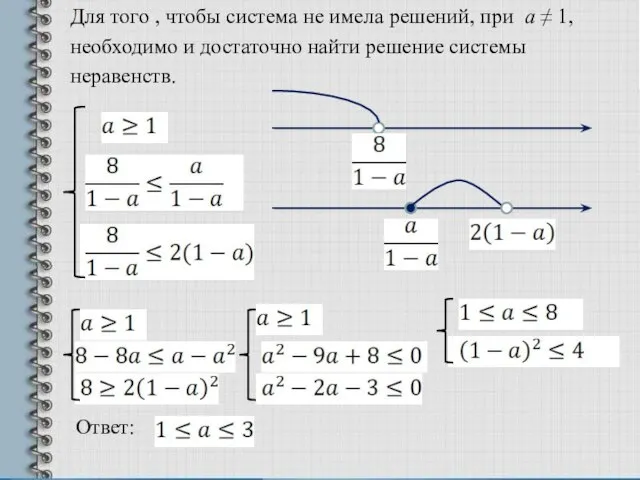
Для того , чтобы система не имела решений, при а  1,
необходимо и достаточно найти решение системы
неравенств.
Ответ:

№ 2. Найти все значения а, при каждом из которых график
функции пересекает ось абсцисс более чем в двух различных
точках.
Решение.
Рассмотрим вспомогательную функцию
.
График функции f(x) пересекает ось абсцисс в трёх или
более точках, если уравнение g(x) = а имеет более двух
различных корней.
Построим график функции g(x) .

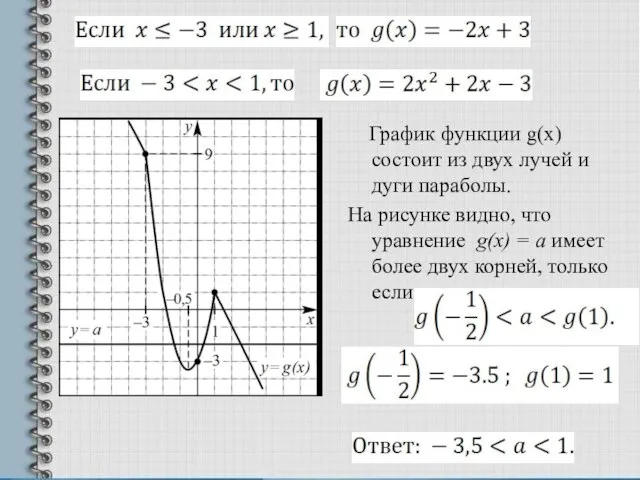
График функции g(x) состоит из двух лучей и дуги параболы.
На рисунке видно, что уравнение g(x) = а имеет более двух корней, только если:

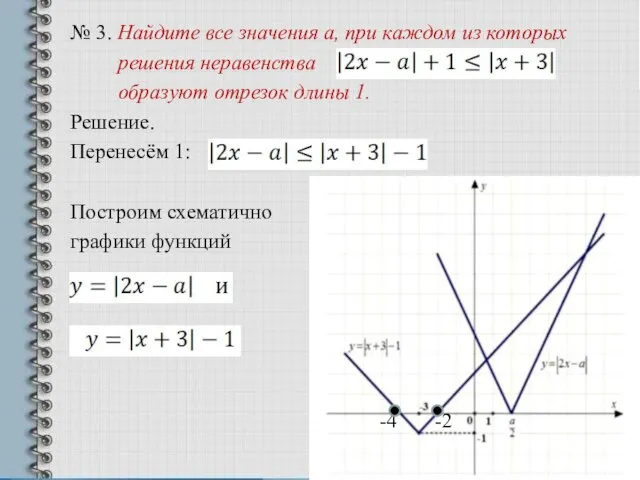
№ 3. Найдите все значения а, при каждом из которых
решения неравенства
образуют отрезок длины 1.
Решение.
Перенесём 1:
Построим схематично
графики функций
-4 -2

На рисунке видно, что неравенство
имеет решения только при .
1 случай
Решения образуют отрезок длины 1, если