Слайд 2Сфери застосування алгоритмів пошуку найкоротших шляхів
Пошук шляхів на мапах міст та країн
Пошук

маршрутів для передачі даних у мережах
Пошук маршрутів у інших задачах, де доцільно використовувати графи
Слайд 3Види алгоритмів пошуку найкоротших шляхів
Пошук шляху із однієї заданої точки в іншу

(алгоритм A*, etc)
Пошук шляхів із однієї заданої точки до усіх інших (алгоритм Дейкстри, алгоритм Белмана-Форда, etc)
Пошук шляхів між усіма парами точок на графі(алгоритм Флойда-Уоршала, алгоритм Джонсона, etc)
Слайд 4Постановка завдання
Розробити алгоритм пошуку найкоротших шляхів для кожної пари точок на графі

із кластерною топологією
Розроблений алгоритм повинен мати меншу за
складність на графі із кластерною топологією
Слайд 5Алгоритм Флойда-Уоршала
Базується на переборі усіх вершин i, j, k та перевірці умови:
Якщо

найкоротший шлях між i та j проходить через вершину k, то відстані від i до k та від j до k додаються
Інакше обирається інша k та продовжується пошук
Пункти 1 та 2 повторюються у циклі по усьому графу
Слайд 6Існуючі спроби рішень
Паралелізація алгоритму на декількох процесорах
Модифікації алгоритму
Рекурсивне обрання підматриць, відновлення

результату через FMM
Слайд 7Кластерна топологія графів
У звичайному графі вершини
зв'язані одна з одною як завгодно,
без

строгого порядку.
Під кластерною топологією будемо
розуміти існування угруповання
вершин на графі, зв’язаних одна з
одною значно більшою кількістю
ребер, ніж із іншими такими
угрупованнями.
Слайд 8Ідея алгоритму
Алгоритм базується на принципі divide and conquer - розділяй та володарюй.
Розіб’ємо

задачу на підзадачи, що будуть мати меншу розмірність, а потім проведемо певні дії для одержання суцільного результату
Слайд 9Зовнішній каркас графа
За умовою наявності кластерної топології, лише через малу кількість вершин
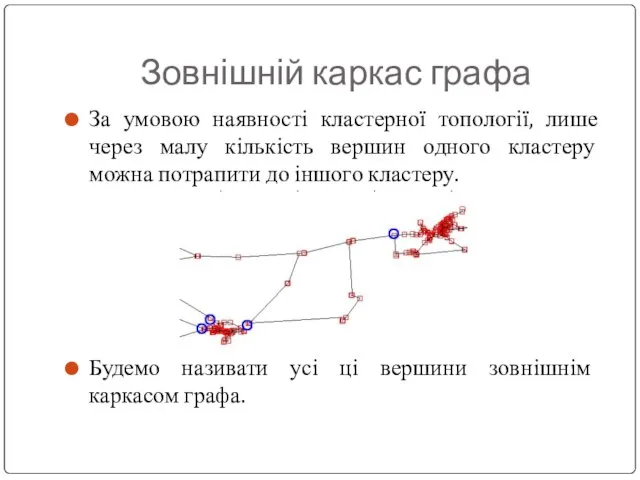
одного кластеру можна потрапити до іншого кластеру.
Будемо називати усі ці вершини зовнішнім каркасом графа.
Слайд 10Опис алгоритму
Знаходження усіх найкоротших шляхів всередині кожного з кластерів
Знаходження усіх найкоротших шляхів

на зовнішньому каркасі графа
Знаходження усіх найкоротших шляхів між точками з одного кластеру до точок з кожного іншого кластеру
Слайд 11Математична оцінка складності алгоритму
Позначення:
Кількість вершин у всьому графі – N
Кількість кластерів –

К
Кількість вершин у i-тому кластері графа –
(де i = 1..K )
Кількість зовнішніх точок – op
Кількість зовнішніх шляхів – ops
Слайд 12Математична оцінка складності алгоритму
Для кожного кластера застосувати алгоритм Флойда-Уоршала –
Для зовнішніх точок

застосувати алгоритм Флойда-Уоршала –
Пошук шляхів між кластерами –
Результуюча формула:
Слайд 13Аналіз моделі
Спрощена оцінка при гіпотезі рівновеликих кластерів:
Підвищення ефективної кількості зовнішніх точок
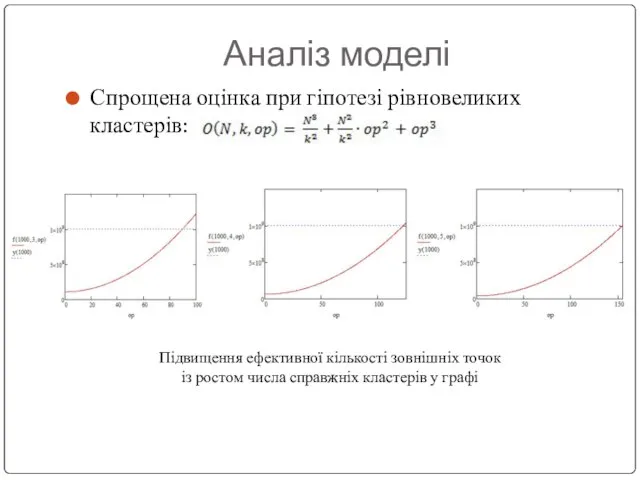
із ростом числа справжніх кластерів у графі
Слайд 14Аналіз моделі
Зменшення долі ефективної кількості зовнішніх вершин у графі залежно від кількості
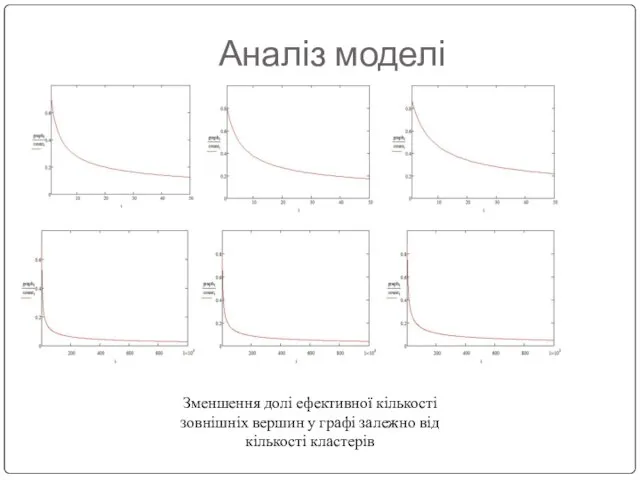
кластерів
Слайд 15Вибір мови програмування
Враховуючи основну вимогу до алгоритму – швидкодію, для реалізації було

вирішено обрати мову С++
Переваги С++:
Відсутність віртуального середовища обробки
Прямі операції з пам'яттю на рівні мови
Наявність допоміжних алгоритмів STL
Слайд 16Результати роботи програми
На вхід було запропоновано:
Граф із більш ніж 1800 точок мапи

України
Автоматично згенеровані графи
На виході було отримано:
Однакові матриці шляхів за звичайним алгоритмом Флойда-Уоршала та розробленою модифікацією
Час виконання модифікованого алгоритму виявився меншим при вдало обраних кластерах
Слайд 17Фрагмент таблиці тестувань часу роботи
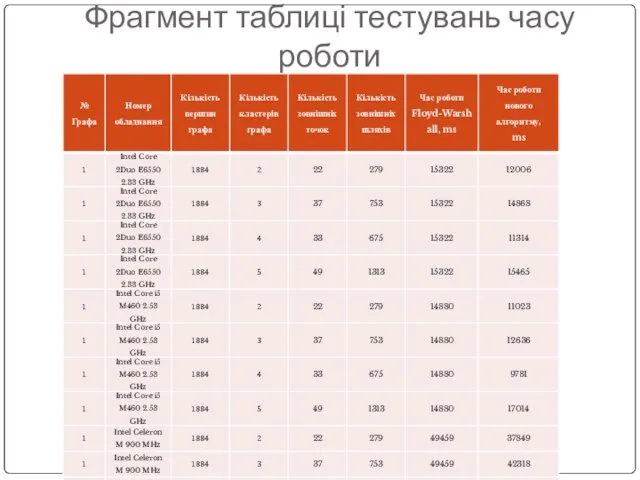
Слайд 18Висновки
Реалізовано алгоритм пошуку найкоротших шляхів між усіма парами точок на графі із

кластерною топологією.
Проведено тестування, в ході якого виявлено зменшення часу виконання у модифікованому алгоритмі.
Приведено повну та спрощену оцінки складності алгоритму, на базі спрощеної проведено аналіз алгоритму.
Результати роботи можуть бути використані у будь-якій сфері, де встає необхідність пошуку найкоротших шляхів на графі, якщо його топологія кластерна.
Слайд 21Недоліки автоматичних алгоритмів кластеризації у розглянутій задачі
Невідома кількість кроків => обчислювальна складність

(k-means, forel, etc)
Невідповідність початковим припущенням алгоритмів реальних графів (EM, SEM, etc)
Відома занадто велика складність алгоритмів (KRAB, etc)
Невідповідність визначенню кластерної топології(найкоротший незамкнений шлях)



















 Возрождение
Возрождение Презентация на тему Моя семья
Презентация на тему Моя семья Я тінь Анни Кареніної. Невід'ємна частинка її життя та смерті
Я тінь Анни Кареніної. Невід'ємна частинка її життя та смерті Изобразительное искусство
Изобразительное искусство Требования к степени очистки сточных вод при их отведении в поверхностные водные объекты
Требования к степени очистки сточных вод при их отведении в поверхностные водные объекты Бочки
Бочки 20170929_trebovaniya_k_kimam_-_kopiya
20170929_trebovaniya_k_kimam_-_kopiya Специальные конструкционные стали
Специальные конструкционные стали Фердинанд де Соссюр
Фердинанд де Соссюр Информационные процессы
Информационные процессы Факторы размещения предприятий черной и цветной металлургии
Факторы размещения предприятий черной и цветной металлургии Бытие как тема философии
Бытие как тема философии Авторское право и смежные права
Авторское право и смежные права Summer Dreams
Summer Dreams  Экскурсия на ТЭЦ-1 г. Казани
Экскурсия на ТЭЦ-1 г. Казани Нашествие с Востока Почему монголо – татары победили русских князей?
Нашествие с Востока Почему монголо – татары победили русских князей? Пример организации контроля доступа на территорию ЖК Триумф Палас
Пример организации контроля доступа на территорию ЖК Триумф Палас ОБЩЕУЧЕБНЫЕ УМЕНИЯ И НАВЫКИ КАК ЭЛЕМЕНТЫ ОЦЕНИВАНИЯ В НОВЫХ СТАНДАРТАХ ОБРАЗОВАНИЯ
ОБЩЕУЧЕБНЫЕ УМЕНИЯ И НАВЫКИ КАК ЭЛЕМЕНТЫ ОЦЕНИВАНИЯ В НОВЫХ СТАНДАРТАХ ОБРАЗОВАНИЯ Презентация на тему Грамматика со Смешариками
Презентация на тему Грамматика со Смешариками Применение нитратов
Применение нитратов Осударственный информационный ресурс бухгалтерской (финансовой) отчетности
Осударственный информационный ресурс бухгалтерской (финансовой) отчетности Консультирование истеричных личностей
Консультирование истеричных личностей Презентация Ветер
Презентация Ветер Деепричастный оборот
Деепричастный оборот Нормативно-правовое обеспечение ВФСК ГТО
Нормативно-правовое обеспечение ВФСК ГТО Презентация на тему Предмет философии
Презентация на тему Предмет философии Афганистан
Афганистан конструирование моделирование
конструирование моделирование