Презентация на тему Замечательные точки треугольника Свойство биссектрисы угла

Цели урока:
Рассмотреть теорему о свойстве биссектрисы угла и её следствие.
Учить применять данные теоремы и следствие при решении задач.
Формировать умения применять известные знания в незнакомой ситуации, сравнивать, анализировать, обобщать.
Продолжать развивать познавательную активность, умение формулировать свои выводы и доказывать их.
Воспитывать уверенность в себе, познавательный интерес.

Исторически геометрия начиналась с треугольника, поэтому вот уже два с половиной тысячелетия треугольник является символом геометрии.
Удивительно, но треугольник, несмотря на свою кажущуюся простоту, является неисчерпаемым объектом изучения - никто даже в наше время не осмелится сказать, что изучил и знает все свойства треугольника.

А какие треугольники знаете вы?
Остроугольный, прямоугольный, равнобедренный, равносторонний…
треугольник египетский,
треугольник Паскаля,
треугольник Рёло,
Бермудский треугольник
треугольник Пенроуза,

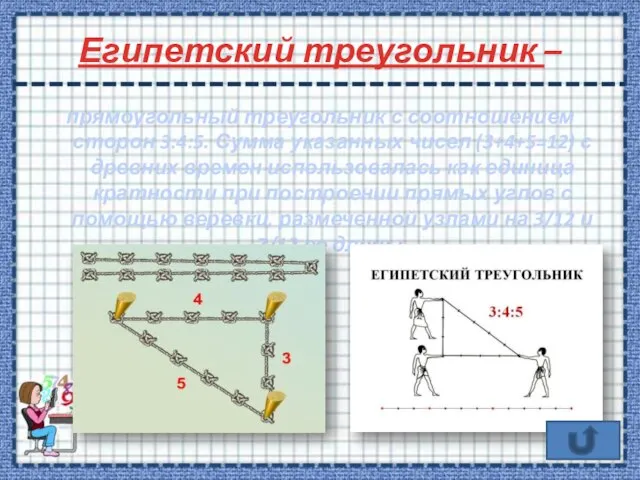
Египетский треугольник –
прямоугольный треугольник с соотношением сторон 3:4:5. Сумма указанных чисел (3+4+5=12) с древних времен использовалась как единица кратности при построении прямых углов с помощью веревки, размеченной узлами на 3/12 и 7/12 ее длины.

Треугольник Паскаля
В этом треугольнике на вершине и по бокам стоят единицы.
Каждое число, которое находится внутри этого треугольника,
равно сумме двух
расположенных
над ним чисел.

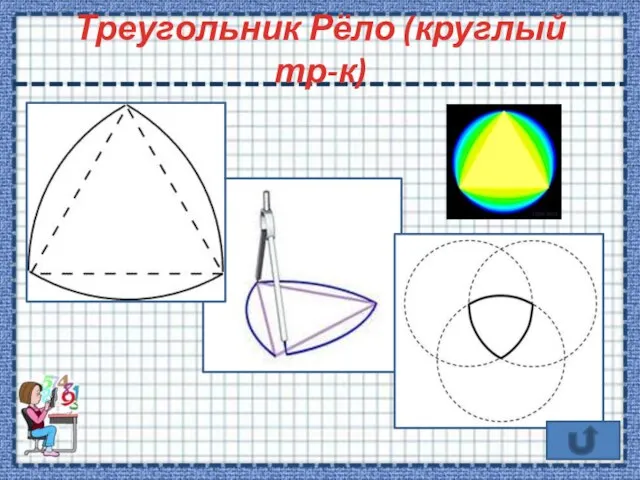
Треугольник Рёло (круглый тр-к)

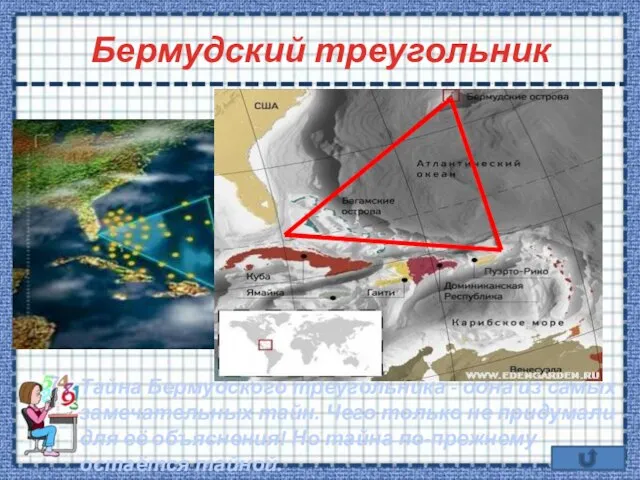
Бермудский треугольник
Тайна Бермудского треугольника - одна из самых замечательных тайн. Чего только не придумали для её объяснения! Но тайна по-прежнему остаётся тайной.

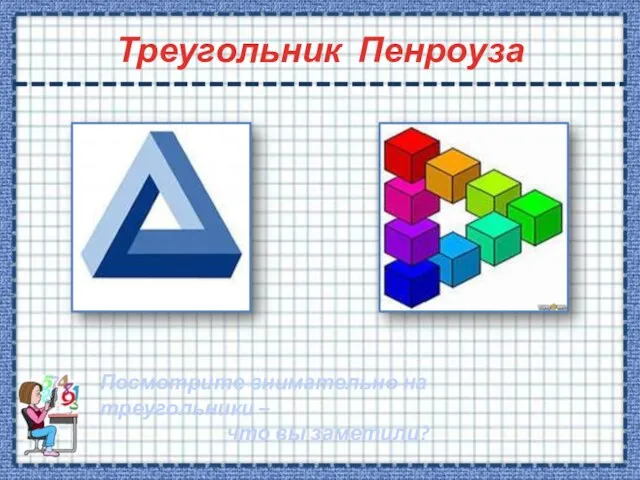
Треугольник Пенроуза
Посмотрите внимательно на треугольники –
что вы заметили?

Интересно!
13-метровую скульптуру
треугольника Пенроуза
(невозможного треугольника)
воздвигли в 1999 году в городе
Перт (Австралия).
Но это только вид с этой стороны!
В действительности
"скульптура" выглядит
вот так:

C каждым треугольником связаны четыре точки:
• точка пересечения медиан;
• точка пересечения биссектрис;
• точка пересечения серединных перпендикуляров;
• точка пересечения высот.
Эти четыре точки называют
замечательными точками треугольника.
Почему они «Замечательные»?
Это нам и предстоит узнать на ближайших уроках.

Свойство биссектрисы
Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон.
Обратно:
Каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе.

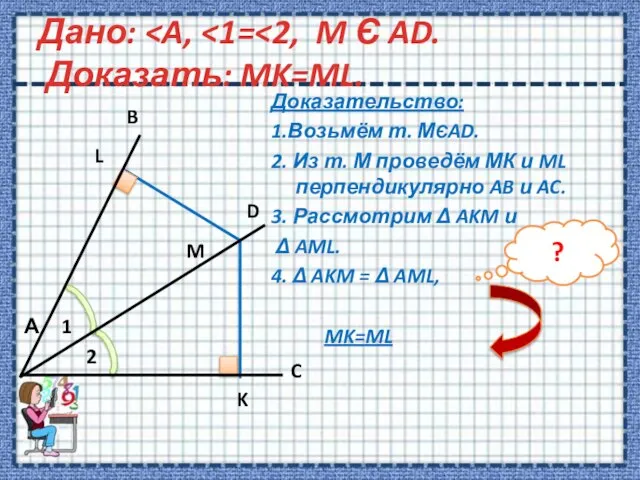
Дано:
Доказательство:
1.Возьмём т. МЄAD.
2. Из т. М проведём МК и ML перпендикулярно AB и AC.
3. Рассмотрим Δ AKM и
Δ AML.
4. Δ AKM = Δ AML,
MK=ML
?
А
2
1

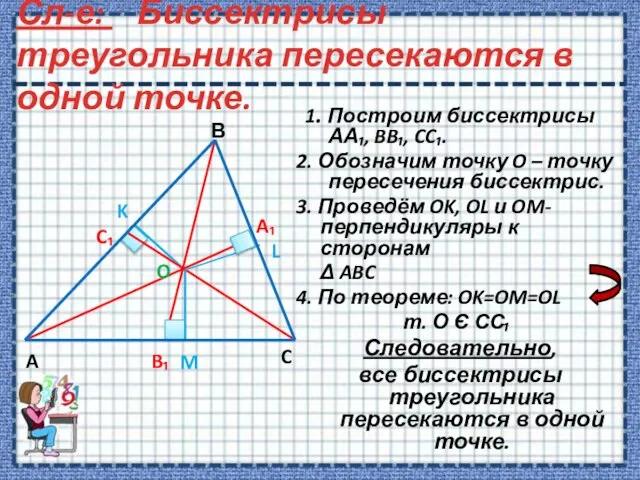
Сл-е: Биссектрисы треугольника пересекаются в одной точке.
1. Построим биссектрисы АА₁, BB₁, CC₁.
2. Обозначим точку O – точку пересечения биссектрис.
3. Проведём OK, OL и OM-перпендикуляры к сторонам
Δ ABC
4. По теореме: OK=OM=OL
т. О Є СС₁
Следовательно,
все биссектрисы треугольника пересекаются в одной точке.
O

№ 676 б
Cтороны угла А, равного 90°, касаются окружности
с центром О и радиусом r, ОА = 14 дм.
Найдите r.

Решение:
Проведём радиусы OP и OH из центра окружности в точки касания.
OP и AP, OH и AH
перпендикулярны
3. AO – биссектриса угла
4. Δ AOP – прямоугольный.
По теореме Пифагора:
AO²=OP²+AP²
AO²=r²+r²,
2r²=14², r=7√2.
Ответ: r=7√2дм.
№ 676 б

№678 а- самопроверка
Дано: ∆АВС, АА1 и ВВ1 биссектрисы углов А и В . < АМВ = 136° .
Найти: < АСМ, < ВСМ.
Решение:
Ответ: 46°.
№678 а- самостоятельно

Что нового я узнал
сегодня на уроке?
Что было особенно интересным
и познавательным?

Домашнее задание:
Вопросы 15, 16, с. 187; №№ 676 (а), 678 (б).

Использованные ресурсы:
Учебник «Геометрия 7-9»; авт: Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина. М., Просвещение, 2007г.
Рисунки треугольников:
Треугольник Рёло:
http://upload.wikimedia.org/wikipedia/commons/c/cf/ReuleauxTriangle.png
http://haritonenko.okis.ru/img/haritonenko/622_4413_1296341088.jpg
http://sibac.info/files/2013_05_07_SchoolNatur/2_Artyushkin.files/image001.jpg
http://commons.wikimedia.org/wiki/File:Mod_Itten_Reuleaux_Triangle_LSSA_256col.gif?uselang=ru
Треугольник Пенроуза:
http://eti.ru/uploads/posts/2011-08/1312994233_glaza11.jpg
http://areeweb.polito.it/didattica/polymath/htmlS/argoment/ParoleMate/Nov_07/Img/Rettangolo.jpg
http://illjuzija.ru/wp-content/uploads/2010/10/skulptura-tryeugolnik-penrouza.jpg
http://illjuzija.ru/wp-content/uploads/2010/10/s-storony-skulptura-tryeugolnik-penrouza-2-e1287403846663.jpg
Треугольник Паскаля:
http://sbirgells.files.wordpress.com/2010/07/pascals_triangle.gif?w=252&h=253
Египетский: http://lib.convdocs.org/pars_docs/refs/252/251618/251618_html_m37e3f8ae.jpg
http://festival.1september.ru/articles/503174/img10.jpg

Использованные ресурсы:
Бермудский треугольник:
http://sobaka.com.ua/c/olds/sobaka/1276506089_0.jpg
http://pirates-life.ru/_fr/9/2824012.jpg
Раскрытая книга:
http://images.funadvice.com/photo/49/photo-book_published_large.jpg
Учебник геометрии: http://www.pomogala.ru/matematika_images/geometry_7_9_atanasyan.JPG
Рисунок треугольника:
http://domsnov.ru/foto/treugolnik.jpg
http://www.clker.com/cliparts/9/a/c/3/11971494591216069200nlyl_orange_triangle.svg.hi.png
Картинка слайда рефлексии:
http://forum.touki.ru/gallery/4d170b90f1d04.png
Тетради:
http://www.orshanka.by/wp-content/uploads/2010/08/Colorful-notebooks-and-pen.jpg
Школьные принадлежности:
http://detsad38.info/metod/img/izonit7.jpg
Знаки вопроса:
http://i.stupenki-studio.ru/u/28/55d73e9aac11e2b7018737826c674f/-/лог2.jpg