Презентация по геометрии на тему: «Зеркальная симметрия» Учеников 11 «А» класса Амбарцумян Карины Качановой С

Определение: Зеркальной симметрией называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей относительно плоскости α точку М1.
Движение-это отображение плоскости на себя, сохраняющее расстояние между точками.
М
М1
α
Примеры: шар(сфера) шар(сфера) - центром симметрии является центр шара; прямая призма обладает зеркальной симметрией - плоскость симметрии параллельна её основаниям и расположена на одинаковом расстоянии между ними.
α

Теорема: Зеркальная симметрия является движением.
М
М1
y
z
x
Дано: М(x,y,z)=А(x,y,z)
M1(x1,y1,z1)=A1(x1,y1,z1),
B(x2,y2,z2).
M симметр. М1
Т. М не лежит в пл.Oxy
Доказать: МB=М1B1
Док-во: по фор-ле коорд.серед. отрезка (z+z1)/2=0, z1= - z.
ММ1 ║ Oz => x1=x, y1=y.
Рассмотрим 2 точки: А(x1,y1,z1) и B(x2,y2,z2)
По фор-ле расст. между 2 точками: AB=√ (x2-x1)2+(y2-y1)2+(z2-z1)2
A1B1= √ (x2-x1)2+(y2-y1)2+(-z2+z1)2 =>AB=A1B1
B
B1

Задача: При зеркальной симметрии прямая а отображается на прямую а1.
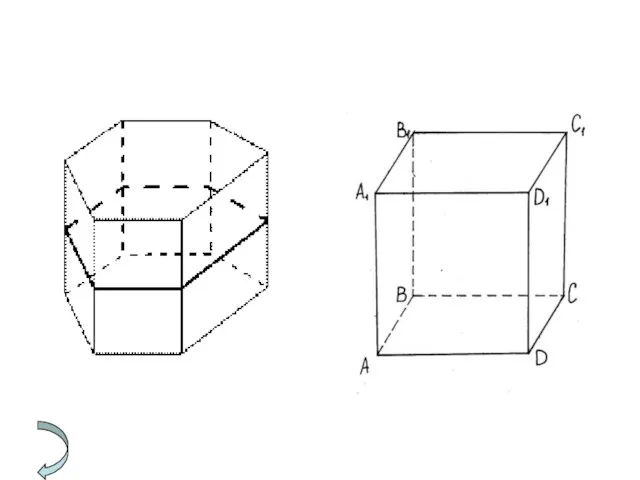
Докажите, что прямые а и а1 лежат в одной плоскости.
а1
а
x
z
y
L
K
A
B
M
N
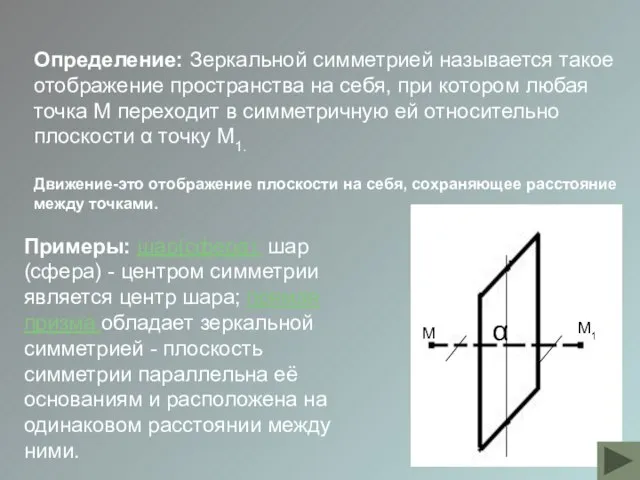
Дано: f(α)- зерк.симметрия
Док-ть: а1,а принадл. α
Док-во: пусть а ║ Oxy. Точки M и L, N и K симметр. MA=AL,NB=BK. Если а ║ Oxy, то
MA=AL=NB=BK. Т.к. две прямые, перпенд. плоскости, между собой ║,то ML ║NK.
ML=NK и MNKL – прямоугольник, => LK ║ MN
Или а ║а1. А ║ прямые лежат в одной плоскости.
Если а ║ Oxy,то она ∩ ее в т. P. При симметрии т. P переходит в себя(т.к. она лежит а пл. Oxy. Значит,p принадлежит
а1. Т.е. прямые а и а1 имеют общ.точку и лежат в одной плоскости.

ПРИМЕРЫ.