Презентация выступления на научной конференции по теме «Формирование комбинаторного мышления школьников V – VII классов»

Проблемная задача № 1: Сколькими способами шашка, стоящая в левом нижнем углу может пройти в дамки?
Вводные задачи: 1) Из точки А надо попасть в точку В, двигаясь только вправо и вверх. Сколькими способами можно это сделать?
А
В
А
В

Вводные задачи: 2)Сколькими способами можно прочитать слово «МАРШРУТ»?

Решение вводных задач №2

Обобщение первой проблемной задачи
Какую букву надо вырезать, чтобы число способов прочтения слова «МАРШРУТ» было равным 171?
Придумайте авторскую задачу.

Решение обобщенной задачи: 267-8·12=171
1
5
2
35
13
267
96
3
1
22
8
у171
61
1
1
75
26
9
3
1
27
9
3
1
3
1
9
3

Решение проблемной задачи №1

Проблемная задача №2
На столе лежит 2001 монета. Двое играют в следующую игру: ходят по очереди, за ход первый может взять со стола любое нечетное число монетот1 до 99, второй – любое четное от 2 до 100. Проигрывает тот, ко не может сделать ход. Кто выиграет при правильной игре? (Из городской олимпиады 2001-2002 учебного года, 9 класс).

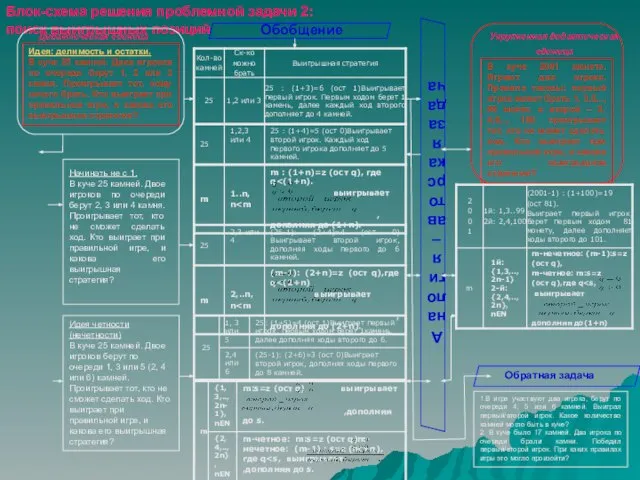
Блок-схема решения проблемной задачи 2: поиск выигрышных позиций
Идея четности (нечетности)
В куче 25 камней. Двое игроков берут по очереди 1, 3 или 5 (2, 4 или 6) камней. Проигрывает тот, кто не сможет сделать ход. Кто выиграет при правильной игре, и какова его выигрышная стратегия?
1.В игре участвуют два игрока, берут по очереди 4, 5 или 6 камней. Выиграл первый/второй игрок. Какое количество камней могло быть в куче?
2. В куче было 17 камней. Два игрока по очереди брали камни. Победил первый/второй игрок. При каких правилах игры это могло произойти?

Проблемная задача № 3: Магические квадраты
Магические квадраты 3 порядка:
1) 45/3=15
2) составляем тройки (всего 8):
1, 5, 9 2, 6, 7
1, 6, 8 3, 4, 8
2, 4, 9 3, 5, 7
2, 5, 8 4, 5, 6

Технология составления магических квадратов нечетного порядка

Технология составления магического квадрата четвертого порядка

Комбинаторика на шахматной доске
1) Сколькими способами шашка, стоящая в левом нижнем углу может пройти в дамки?
2) Какое наибольшее количество ферзей можно поставить на шах матную доску так, чтобы они не били друг друга? Покажите один из способов такой расстановки. Сколькими способами можно это сделать?
3) Сколькими способами можно поставить на шахматной доске двух коней так, чтобы они не били друг друга?
4) Обобщите задачи. Придумайте авторские задачи.

Решение задачи: Сколькими способами можно поставить на шахматной доске двух коней так, чтобы они не били друг друга?
1) 4·(64-3)=244
2) 8·(64-4)=480
3) 20·(64-5)=1180
4) 16·(64-7)=912
5) 16·(64-9)=880
6) (244+480+1180+
+912+880)/2=1848