Презентация Основы ТВ

ЗАДАЧА ИЗ АНАЛИЗА ЛОТЕРЕИ
Вы – организатор лотереи, в которой разыгрывается автомобиль стоимостью 2 миллиона рублей. Для розыгрыша Вы выпустили карточки, на каждой из которых 20 клеточек (10 с буквами
а в т о м о б и л ь и 10 без букв) с покры-тием защитной пленкой. Участник лоте-реи может стереть только 10 любых кле-ток. Какой должна быть минимальная цена за билет и сколько билетов нужно выпустить, чтобы Вы отдали 1 приз и получили прибыль.

ИСТОРИЯ ВОЗНИКНОВЕНИЯ
И РАЗВИТИЕ ТЕОРИИ ВЕРОЯТНОСТЕЙ

Случайные явления имеют свои зако-
ны, которые начинают проявляться при многократном повторении. Такие законо-мерности изучает теория вероятностей
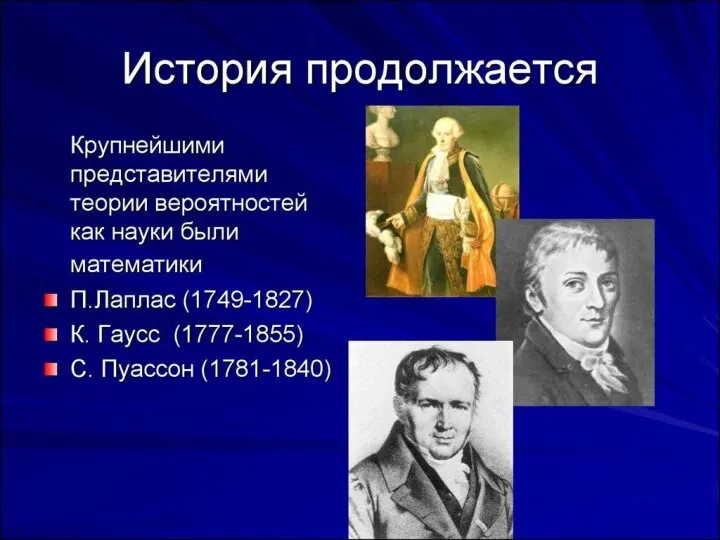
«Теория вероятностей есть в сущности не что иное, как здравый смысл, сведенный к исчислению»
Лаплас

ГАЛИЛЕО ГАЛИЛЕЙ (1564-1642)

В 1846 ГОДУ ВЫШЛА КНИГА РУССКОГО МАТЕМАТИКА В.Я.БУНЯКОВСКОГО, ЭТО БЫЛ ПЕРВЫЙ УЧЕБНИК ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ, ПО КОТОРОМУ УЧИЛИСЬ ЧЕБЫШЕВ, МАРКОВ, ЛЯПУНОВ И ДРУГИЕ

ТЕОРЕМА СУММЫ
ВЕРОЯТНОСТЕЙ СОБЫТИЙ
Суммой A + B событий A и B называется событие, состоящее в появлении события А, или события В, или обоих этих событий.
Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий: Р(А+В)=Р(А)+ Р(В)

ТЕОРЕМА УМНОЖЕНИЯ НЕЗАВИСИМЫХ СОБЫТИЙ
Произведением A1∙ A2 событий A1 и A2 называется событие, состоящее в одновременном появлении двух этих событий (первого и второго)
Вероятность произведения двух независимых событий A1 и A2 равна произведению их вероятностей:
P(A1∙ A2) = P(A1)∙P(A2)

ЗАДАЧА 1
Коэффициенты использования рабочего времени у двух приборов соответственно равны 0,8 и 0,6. Считая, что остановки в работе каждого прибора возникают случайно и независимо друг от друга, определить вероятность:
1) времени совместной работы приборов;
2) времени остановки обоих приборов.

ЗАДАЧА 2
В первом ящике 1 белый и 5 чер-ных шаров, во втором 8 белых и 4 черных шара. Из каждого ящи-ка вынули по шару. Найти вероят-ность того, что один из вынутых шаров белый, а другой – черный.

ТЕОРЕМА ПРОИЗВЕДЕНИЯ ЗАВИСИМЫХ СОБЫТИЙ
Условной вероятностью Р(В/А) называется вероятность события В при условии, что событие А уже произошло
Вероятность появления двух зависи-мых событий равна произведению ве-роятности одного из них на условную вероятность другого при условии, что первое событие уже наступило
Р(А∙В) = Р(А)∙Р(В/А)

ЗАДАЧА 3
Из колоды в 36 карт достали 3 кар-
ты. Какова вероятность, что этими картами окажутся 2 дамы и король?

ЗАДАЧА 4
Из трёх студентов, пришедших на экзамен
1-ый подготовился отлично и может ответить на все 16 вопросов, 2-ой подготовился хорошо и может ответить на 12 вопросов из 16, третий подготовился удовлетворительно и знает ответы только на половину вопросов. Приглашенный первым студент ответил на 3 вопроса и успешно сдал экзамен. Какова вероятность того, что приглашенный студент был:
1 вариант) хорошистом;
2 вариант) троечником ?

ЗАДАЧА 5
Вы – организатор лотереи, в которой разы-грывается автомобиль стоимостью 2 мил-лиона рублей. Для розыгрыша Вы выпусти-ли карточки, на каждой из которых 20 кле-точек (10 с буквами а в т о м о б и л ь и 10 без букв) с покрытием защитной пленкой. Участник лотереи может стереть только 10 любых клеток. Какой должна быть мини-мальная цена за билет и сколько билетов нужно выпустить, чтобы Вы отдали 1 приз и получили прибыль.