Презентація 10 клас Урок 18

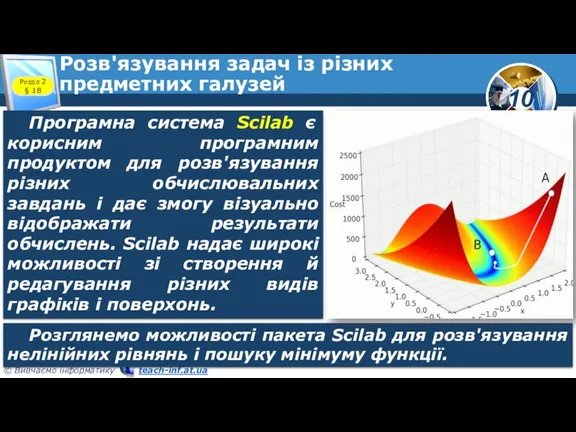
Розв'язування задач із різних предметних галузей
Розділ 2 § 18
Програмна система Scilab є корисним програмним продуктом для розв'язування різних обчислювальних завдань і дає змогу візуально відображати результати обчислень. Scilab надає широкі можливості зі створення й редагування різних видів графіків і поверхонь.
Розглянемо можливості пакета Scilab для розв'язування нелінійних рівнянь і пошуку мінімуму функції.

Побудова графіків
функції однієї змінної
Розділ 2 § 18
Scilab містить набір функцій для графічного подання інформації. Функція plot призначена для побудови графіка функції у = f(x). Загальний вигляд команди:
plot (х, у)
Вектор значень х має бути заданий перед використанням у функції plot.
два вектори однакового розміру.
х, у

Побудова графіків
функції однієї змінної
Розділ 2 § 18
Задати заголовок графіка, найменування осей можна за допомогою функції:
xtitle(caption, хсар, усар)
заголовок графіка, хсар, усар — підписи осей Х, Y.
caption

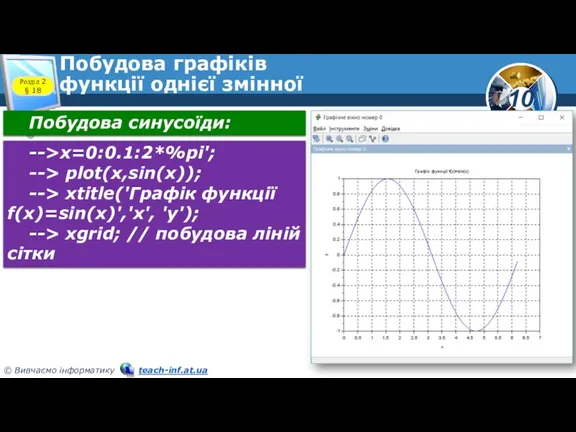
Побудова графіків
функції однієї змінної
Розділ 2 § 18
Побудова синусоїди:
-->x=0:0.1:2*%pi';
--> plot(x,sin(x));
--> xtitle('Графік функції f(x)=sin(x)','x', 'у');
--> xgrid; // побудова ліній сітки

Розв'язування нелінійних рівнянь
Розділ 2 § 18
Ми вже розглянули функцію roots(f(x)), яку застосовують для пошуку коренів рівняння f(x) = 0, де f(x) є поліномом.
Але існують рівняння, які не можна розв'язувати алгебраїчними методами. Для розв'язування таких рівнянь існують методи наближених обчислень.

Розв'язування нелінійних рівнянь
Розділ 2 § 18
Для наближеного обчислення кореня нелінійного рівняння f(x) = 0 спочатку необхідно визначити інтервал [а,b], на якому існує єдиний корінь рівняння. Визначити такий інтервал можна, наприклад, за графіком функції f(x). Після цього в Scilab для розв'язування таких рівнянь застосовують функцію
fsolve(x0,f)
початкове наближення кореня рівняння —
(х0 є [а,b])
х0
функція, що описує ліву частину рівняння
f(x) = 0.
f

Розв'язування нелінійних рівнянь
Розділ 2 § 18
Знайти корінь рівняння х5 — х3 + 1 = 0 на інтервалі
[—1.5;1.5]. Відомо, що в даному інтервалі рівняння має один корінь. Опишемо функцію f(x) = х5 — х3 + 1 , і задамо початкове наближення кореня -1.5:
-->function y=f(x)
-->у=х.^5-х.^3+1;
->endfunction
-->x=fsolve(1.5,f)
->x=fsolve(-1.5,f)
x = -1.2365057
Отримуємо відповідь:

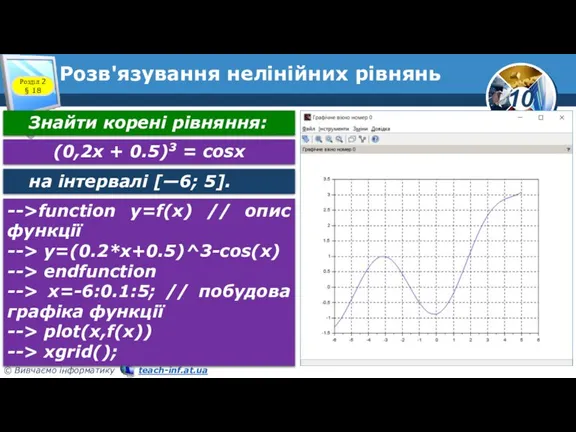
Розв'язування нелінійних рівнянь
Розділ 2 § 18
Знайти корені рівняння:
(0,2х + 0.5)3 = cosx
на інтервалі [—6; 5].
-->function y=f(x) // опис функції
--> y=(0.2*x+0.5)^3-cos(x)
--> endfunction
--> x=-6:0.1:5; // побудова графіка функції
--> plot(x,f(x))
--> xgrid();

Розв'язування нелінійних рівнянь
Розділ 2 § 18
На графіку видно, що на зазначеному інтервалі рівняння має три корені. В такому випадку початкові наближення можна задати у вигляді вектора й викликати функцію один раз:
-->x=fsolve([-5;-2;1],f)
х =
-4.956089
-1.5334163
1.0443216

Пошук мінімуму
функції однієї змінної
Розділ 2 § 18
Розглянемо пошук локального мінімуму функції однієї змінної як найпростішу оптимізаційну задачу.
Для знаходження значення мінімуму функції у Scilab існує функція:
[fmin,xmin]=optim(cst,x0)
Функція повертає значення мінімуму функції (fmin) і точку, в якій функція досягає цього значення (xmin).
масив початкових наближень довжиною n.
х0

Пошук мінімуму
функції однієї змінної
Розділ 2 § 18
Головною особливістю функції optim є структура функції cst, яка має бути такою:
function [f,g,ind]= cst (x,ind)
f=<функція, мінімум якої шукаємо>
g=<похідна функції f>
endfunction
Значення параметра ind є внутрішнім параметром для зв'язку між:
optim
est
і

Пошук мінімуму
функції однієї змінної
Розділ 2 § 18
Знайти мінімум функції f(x) = (0,2x + 0.5)3 — cosx на інтервалі [— 5;5]. Виконаємо команди:
-->function y=fm(x)
-->y=(0.2*x+0.5)^2-cos(x);
-->endfunction
-->function[f,g,ind]=cst(x,ind)
-->f=fm(x)
-->g=numderivative(fm,x)
-->endfunction
-->x0=-2; // Початкове наближення точки мінімуму
-->[fmin,xmin]=optim(cst,xo) // виклик функції optim для пошуку точки (fmin,xmin)
xmin = -0.1861794
fmin = -0.7685680

Пошук мінімуму
функції однієї змінної
Розділ 2 § 18
Для пошуку максимуму функції f(x) треба застосувати функцію optim для функції -f(x).
Як видно з прикладів, перед пошуком коренів нелінійного рівняння або мінімуму функції доцільно побудувати графік функції f(x).
Аналіз графіка функції дає змогу визначити, скільки коренів існує на вказаному інтервалі, дібрати початкове наближення, що суттєво впливає на результат.

Питання для самоперевірки
Розділ 2 § 18
Поясніть алгоритм побудови графіка функції.
Поясніть відмінності між областями застосування функцій roots(f) і fsolve(x,f).
Функцію f(x) описано в такий спосіб:
function y=f (х)
у= х^з +2*х^2 - 3*х+1;
endfunction
Опишіть функцію est, яка буде використана як параметр у разі виклику функції optim(cst,xO), для знаходження значення мінімуму функції f(x).

Домашнє завдання
Проаналізувати
§ 18, ст. 99-104
Розділ 2 § 18

Працюємо за комп’ютером
Практична робота 3
Обчислення статистичних характеристик засобами MS Excel i Scilab
Розділ 2 § 18

Працюємо за комп’ютером
Розділ 2 § 18
Сторінка
103-104