Содержание
- 2. Вычисления корня уравнения f(x)=0 Вычисления на компьютере обладают большей гибкостью, чем привычные всем вычисления в математике.
- 3. Постановка задачи Дано уравнение f(x) = 0 и числа a и b: a f(a) и f(b)
- 4. Алгоритм метода деления отрезка пополам 3) если |a – b| > E, то перейти к пункту
- 5. Когда можно применять метод деления отрезка пополам Что необходимо предварительно сделать, прежде чем применять этот алгоритм
- 7. Скачать презентацию
Слайд 2Вычисления корня уравнения f(x)=0
Вычисления на компьютере обладают большей гибкостью, чем привычные
Вычисления корня уравнения f(x)=0
Вычисления на компьютере обладают большей гибкостью, чем привычные

Однако, во многих случаях, ответ не выражается формулой (например, для корня уравнения cos(x) = x формулы просто нет). Но можно, не выводя точных формул, вычислить корень приближенно, с заданной точностью, например, до 0,0001. Мы рассмотрим один из приближенных методов вычисления корня уравнения – метод деления отрезка пополам.
Слайд 3Постановка задачи
Дано уравнение f(x) = 0 и числа a и b:
Постановка задачи
Дано уравнение f(x) = 0 и числа a и b:

f(a) и f(b) имеют разные знаки на отрезке [a, b], т.е. f(a)* f(b)<0,
а график функции y = f(x) есть непрерывная линия на отрезке [a, b].
В этом случае график функции обязательно пересечет ось OX.
Требуется определить корень уравнения W с точностью E > 0.
Если V–точный корень уравнения f(V) = 0, a < V < b, то требуется найти W: |W – V| < E, a < W < b.
Слайд 4Алгоритм метода деления отрезка пополам
3) если |a – b| > E, то
Алгоритм метода деления отрезка пополам
3) если |a – b| > E, то
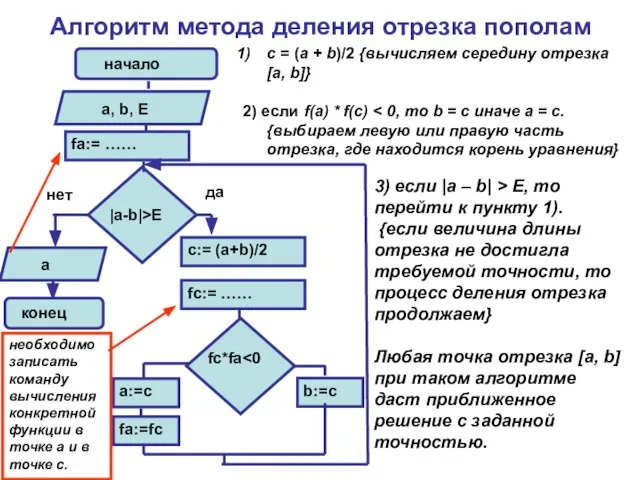
{если величина длины отрезка не достигла требуемой точности, то процесс деления отрезка продолжаем}
Любая точка отрезка [a, b] при таком алгоритме даст приближенное решение с заданной точностью.
c = (a + b)/2 {вычисляем середину отрезка [a, b]}
2) если f(a) * f(с) < 0, то b = c иначе a = c. {выбираем левую или правую часть отрезка, где находится корень уравнения}
необходимо записать команду вычисления конкретной функции в точке a и в точке c.
Слайд 5Когда можно применять метод деления отрезка пополам
Что необходимо предварительно сделать, прежде чем
Когда можно применять метод деления отрезка пополам
Что необходимо предварительно сделать, прежде чем

Необходимо, в первую очередь, проверить, удовлетворяет ли функция постановке задачи: является ли график функции непрерывной линией на отрезке [a, b], разные ли знаки имеет функция на концах отрезка [a, b].
Можно ли применять метод деления отрезка пополам для нахождения корней уравнений, на заданных отрезках
x2 – 5 = 0, [0, 3] (ПО: функция непрерывна на отрезке и f(0) * f(3) < 0, применять метод можно)
sin(x) – 0,2 = 0 [0, /2] (ПО: функция непрерывна на отрезке и f(0) * f( /2) < 0, применять метод можно)
1/(x – 1) [–2, 2] (ПО: функция не существует в точке х=1, применять метод нельзя)
x4 + cos(x) – 2 = 0 [0, 2] (ПО: функция непрерывна на отрезке и f(0)* f(2) < 0, применять метод можно)
x5 – 1 = 0 [–5, 2] (ПО: функция непрерывна на отрезке и f(– 5) * f(2) < 0, применять метод можно)
 Площади многоугольников
Площади многоугольников Победа в Отечественной войне 1812 года
Победа в Отечественной войне 1812 года Правила поведения во время похода
Правила поведения во время похода Кроманьонцы
Кроманьонцы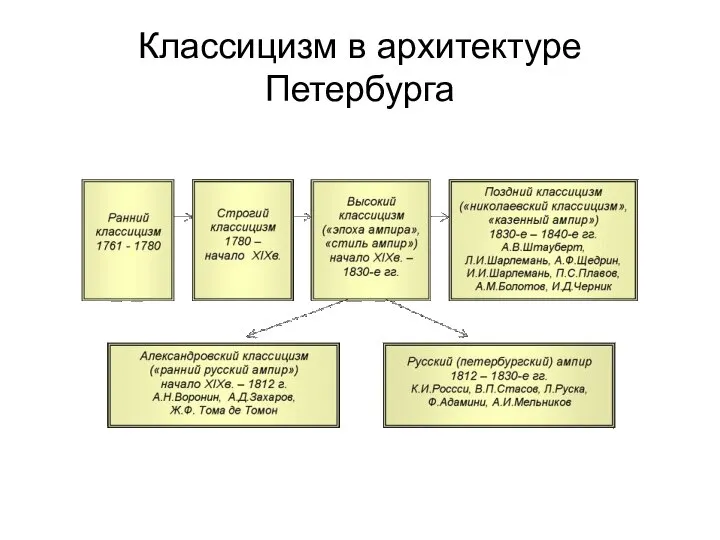 Классицизм в архитектуре Петербурга
Классицизм в архитектуре Петербурга The 10 most popular vehicles in history.
The 10 most popular vehicles in history. Famous Composers
Famous Composers Игра: "Калейдоскоп естественных наук"
Игра: "Калейдоскоп естественных наук" Работа с проволокой
Работа с проволокой Константин Бальмонт
Константин Бальмонт Раздел 6 изм. Замена лампочек
Раздел 6 изм. Замена лампочек 1
1 Виды партнерства и сотрудничества в предпринимательской деятельности
Виды партнерства и сотрудничества в предпринимательской деятельности Построение биссектрисы углагеометрия, 7 класс
Построение биссектрисы углагеометрия, 7 класс Мы во Вселенной
Мы во Вселенной Телеграфная связь
Телеграфная связь Proverbs and sayings
Proverbs and sayings Презентация на тему Режим дня дошкольника
Презентация на тему Режим дня дошкольника Виды туризма по способу передвижения. Краткая характеристика пешего и лыжного туризма
Виды туризма по способу передвижения. Краткая характеристика пешего и лыжного туризма Презентация на тему ПАДЕЖИ Знакомство с падежами имен существительных
Презентация на тему ПАДЕЖИ Знакомство с падежами имен существительных  Таврический дворец
Таврический дворец Жилой комплекс подворья Марфо-Мариинской обители в Севастополе
Жилой комплекс подворья Марфо-Мариинской обители в Севастополе Представление информации
Представление информации Наши зимние забавы
Наши зимние забавы Инновационные решения для распределительных сетей 6 - 35 кВ. ООО Оптиметрик, 2021
Инновационные решения для распределительных сетей 6 - 35 кВ. ООО Оптиметрик, 2021 Шаблон ПРЕЗЕНТАЦИИ к рубежной аттестации 1 курс ОПД-1
Шаблон ПРЕЗЕНТАЦИИ к рубежной аттестации 1 курс ОПД-1 Свойства текстильных волокон. 5 класс
Свойства текстильных волокон. 5 класс Презентация на тему Анализаторы органы чувств
Презентация на тему Анализаторы органы чувств