Слайд 3Задачи по теме 2.
1. Из 1000 собранных на заводе телевизоров 5 штук

бракованных. Эксперт проверяет один наугад выбранный телевизор из этой 1000. Найдите вероятность того, что проверяемый телевизор окажется бракованным.
Слайд 4Задачи по теме 2.
2. В урне 9 красных, 6 жёлтых и 5

зелёных шаров. Из урны наугад достают один шар. Какова вероятность того, что этот шар окажется жёлтым?
Слайд 5Задачи по теме 2.
3. В чемпионате мира участвуют 16 команд. С помощью

жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
Слайд 6Задачи по теме 2.
4. В лыжных гонках участвуют 11 спортсменов из России,

6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
Слайд 7Задачи по теме 2.
5. В чемпионате по футболу участвуют 16 команд, которые

жеребьевкой распределяются на 4 группы: A, B, C и D. Какова вероятность того, что команда России не попадает в группу A?
Слайд 8Задачи по теме 2.
6. На турнир по шахматам прибыло 26 участников в

том числе Коля и Толя. Для проведения жеребьевки первого тура участников случайным образом разбили на две группы по 13 человек. Найти вероятность того, что Коля и Толя попадут в разные группы.
Слайд 9Задачи по теме 2.
7. Механические часы с двенадцатичасовым циферблатом в какой-то момент

сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 7, но не дойдя до отметки 1.
Слайд 10Задачи по теме 2.
Подсказка
При решении задач с монетами число всех возможных

исходов можно посчитать по формуле
п=2ª,
где α –количество бросков
Слайд 11Задачи по теме 2.
8. В случайном эксперименте симметричную монету бросают 2 раза.

Найдите вероятность того, что орел выпадет ровно 1 раз.
Слайд 129. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что

орёл выпадет ровно 2 раза.
Слайд 13Задачи по теме 2.
10. В случайном эксперименте симметричную монету бросают четырежды. Найдите

вероятность того, что решка не выпадет ни разу.
Слайд 14Задачи по теме 2.
Подсказка
При решении задач с кубиками число всех возможных

исходов можно посчитать по формуле
п=6ª,
где α –количество бросков
Слайд 15Задачи по теме 2.
11. Игральную кость бросают дважды. Найдите вероятность того, что

оба раза выпало число, большее 3.
Слайд 16Задачи по теме 2.
12. В случайном эксперименте бросают три игральные кости. Найдите

вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.
Слайд 17
13. Коля выбирает трехзначное число. Найдите вероятность того, что оно делится на

5.
Слайд 18
14. Для экзамена подготовили билеты с номерами от 1 до 50. Какова

вероятность того, что наугад взятый учеником билет имеет однозначный номер?
Слайд 1915. В мешке содержатся жетоны с номерами от 5 до 54 включительно.

Какова вероятность, того, что извлеченный наугад из мешка жетон содержит двузначное число?
Слайд 20
16. Вероятность того, что новая шариковая ручка пишет плохо (или не пишет),

равна 0,19. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Слайд 2117. При изготовлении подшипников диаметром 67 мм вероятность того, что диаметр будет

отличаться от заданного не больше, чем на 0,01 мм, равна 0,965. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 66,99 мм или больше чем 67,01 мм.
Слайд 2218. На экзамене по геометрии школьнику достаётся одна задача из сборника. Вероятность

того, что эта задача по теме «Углы», равна 0,1. Вероятность того, что это окажется задача по теме «Параллелограмм», равна 0,6. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.
Слайд 2319. Вероятность того, что на тесте по биологии учащийся О. верно решит

больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач.






















 12.10.2022_домашнее задание
12.10.2022_домашнее задание Всероссийский конкурс проектов, направленных на решение задач информирования обучающихся к ведению здорового образа жизни
Всероссийский конкурс проектов, направленных на решение задач информирования обучающихся к ведению здорового образа жизни New York
New York Тема занятия: перспектива
Тема занятия: перспектива ГОУ СОШ №706 экспериментальная площадка второго уровня
ГОУ СОШ №706 экспериментальная площадка второго уровня Правила приёма в 2020 году
Правила приёма в 2020 году Собор Парижской Богоматери. Франция - родина готической архитектуры
Собор Парижской Богоматери. Франция - родина готической архитектуры Операционные системы
Операционные системы Отчетно-выборная конференция Студенческого совета Химического факультета МГУ Отчет председателя Студенческого совета Соболева
Отчетно-выборная конференция Студенческого совета Химического факультета МГУ Отчет председателя Студенческого совета Соболева  Самообразование библиотекаря: направления, методы и формы
Самообразование библиотекаря: направления, методы и формы Зачем строят корабли (1 класс)
Зачем строят корабли (1 класс) Базовый элемент: Транзистор
Базовый элемент: Транзистор Практикум в DeFi
Практикум в DeFi РЕЧЬ В ШКОЛЕ
РЕЧЬ В ШКОЛЕ Клуб Веселых Математиков
Клуб Веселых Математиков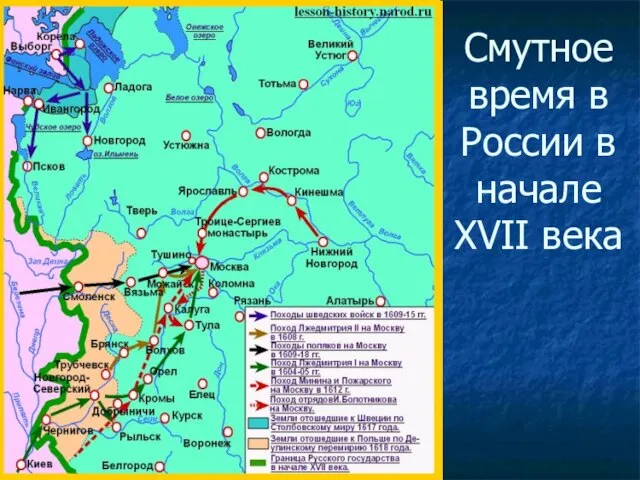 Смутное время в России в начале XVII века
Смутное время в России в начале XVII века Презентация на тему В ботаническом саду
Презентация на тему В ботаническом саду Живопись Леонардо да Винчи
Живопись Леонардо да Винчи Презентация на тему Новый Закон об образовании
Презентация на тему Новый Закон об образовании EU Financial Markets Law
EU Financial Markets Law Презентация на тему Лермонтов «Песня про купца Калашникова…» 8 класс
Презентация на тему Лермонтов «Песня про купца Калашникова…» 8 класс Основы проектирования строительных конструкций
Основы проектирования строительных конструкций ВК.pptx
ВК.pptx Монтаж модульных домов из деревянных конструкций
Монтаж модульных домов из деревянных конструкций Маркетинговый анализ работы веб-студии: ищем способы повышения эффективности работы
Маркетинговый анализ работы веб-студии: ищем способы повышения эффективности работы Рисуем на осенних листах
Рисуем на осенних листах Здоровье человека и окружающая среда
Здоровье человека и окружающая среда Сергей Павлович Королёв
Сергей Павлович Королёв