Применение двумерных диаграмм

Цель занятия:
научиться применять диаграммы в качестве
одного из средств решения некоторых
алгебраических задач

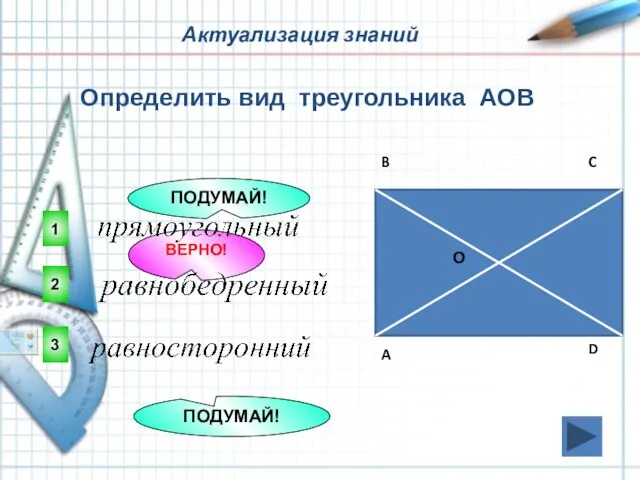
Актуализация знаний
2
ВЕРНО!
1
3
ПОДУМАЙ!
ПОДУМАЙ!
Определить вид треугольника АОВ

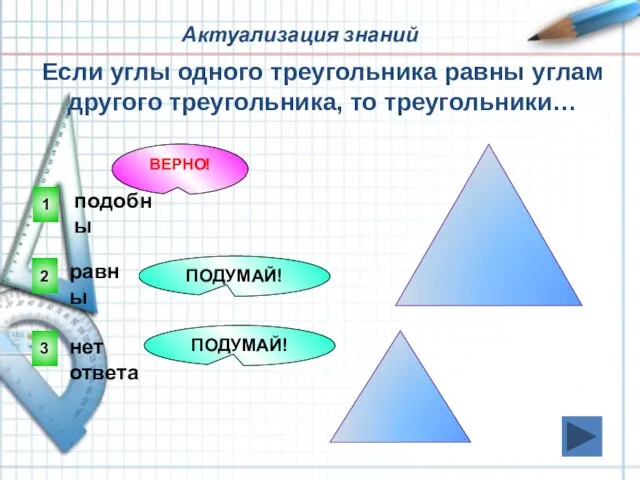
1
ВЕРНО!
2
3
ПОДУМАЙ!
ПОДУМАЙ!
Если углы одного треугольника равны углам другого треугольника, то треугольники…
Актуализация знаний
подобны
равны
нет ответа

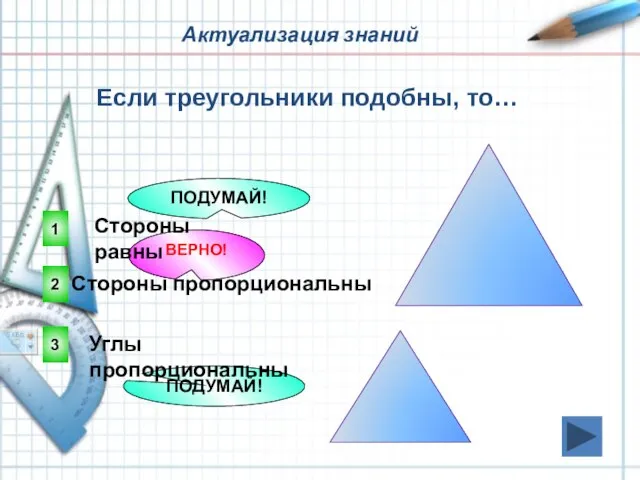
Актуализация знаний
2
ВЕРНО!
1
3
ПОДУМАЙ!
ПОДУМАЙ!
Если треугольники подобны, то…
Стороны пропорциональны
Стороны равны
Углы пропорциональны

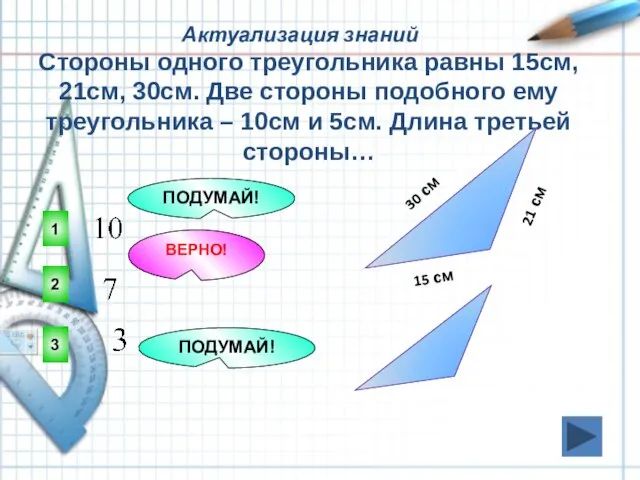
Актуализация знаний
2
ВЕРНО!
1
3
ПОДУМАЙ!
ПОДУМАЙ!
Стороны одного треугольника равны 15см, 21см, 30см. Две стороны подобного ему треугольника – 10см и 5см. Длина третьей стороны…
2
30 см
21 см
15 см

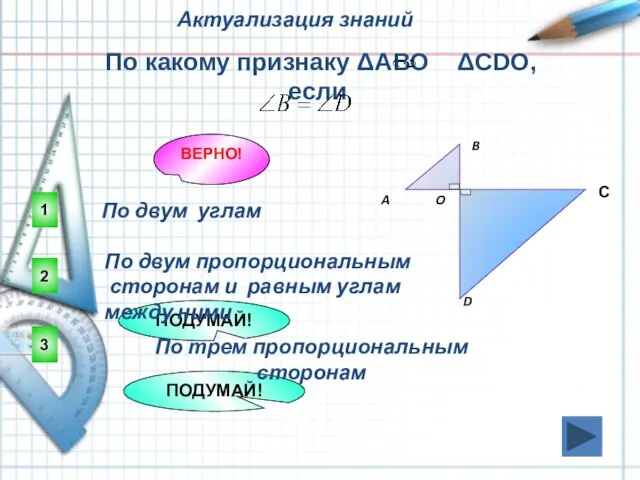
1
ВЕРНО!
2
3
ПОДУМАЙ!
ПОДУМАЙ!
Актуализация знаний
По какому признаку ΔАВО ΔСDO, если
По двум углам
По двум пропорциональным
сторонам и равным углам между ними
По трем пропорциональным сторонам

Погребальная камера гробницы Рамсеса

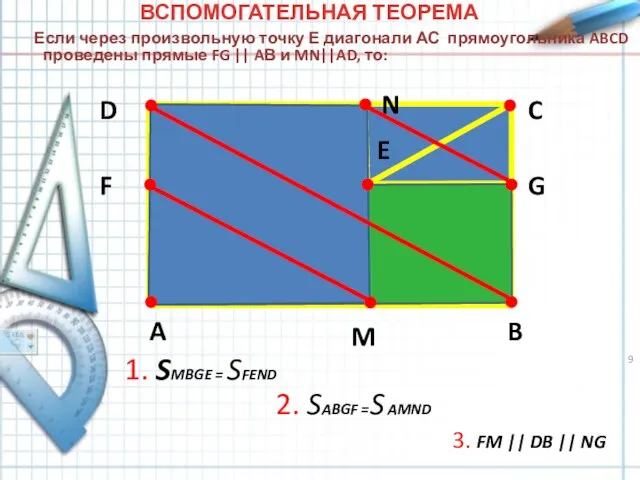
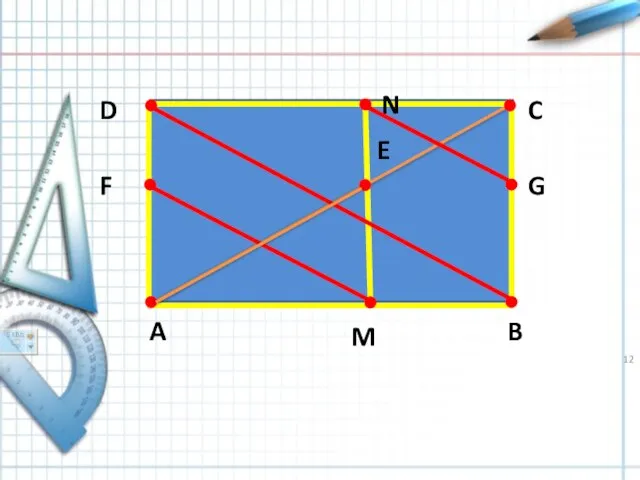
A
B
C
D
E
F
G
M
N
1. SMBGE = SFEND
2. SABGF =S AMND
3. FM || DB || NG
ВСПОМОГАТЕЛЬНАЯ ТЕОРЕМА
Если через произвольную точку Е диагонали АС прямоугольника ABCD проведены прямые FG || AВ и MN||AD, то:

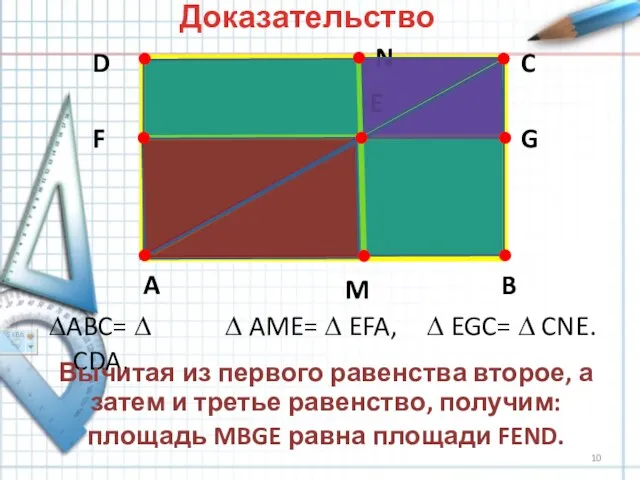
A
B
C
D
E
F
G
M
N
∆ABC= ∆ CDA,
∆ AME= ∆ EFA,
∆ EGC= ∆ CNE.
Вычитая из первого равенства второе, а затем и третье равенство, получим:
площадь MBGE равна площади FEND.
Доказательство

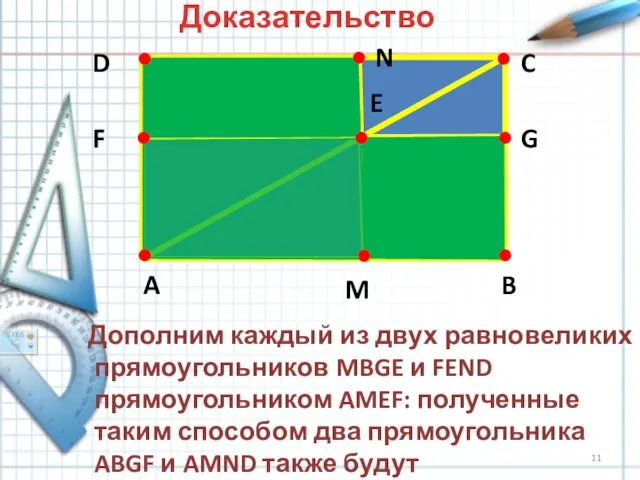
A
B
C
D
E
F
G
M
N
Доказательство
Дополним каждый из двух равновеликих прямоугольников MBGE и FEND прямоугольником AMEF: полученные таким способом два прямоугольника ABGF и AMND также будут равновеликими

A
B
C
D
E
F
G
M
N

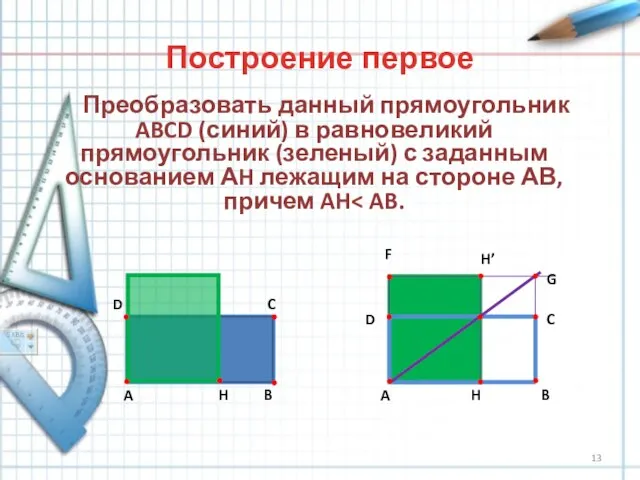
Построение первое
Преобразовать данный прямоугольник ABCD (синий) в равновеликий прямоугольник (зеленый) с заданным основанием АH лежащим на стороне АВ, причем AH< AB.
A
B
C
D
H
A
B
C
D
H
H’
G
F

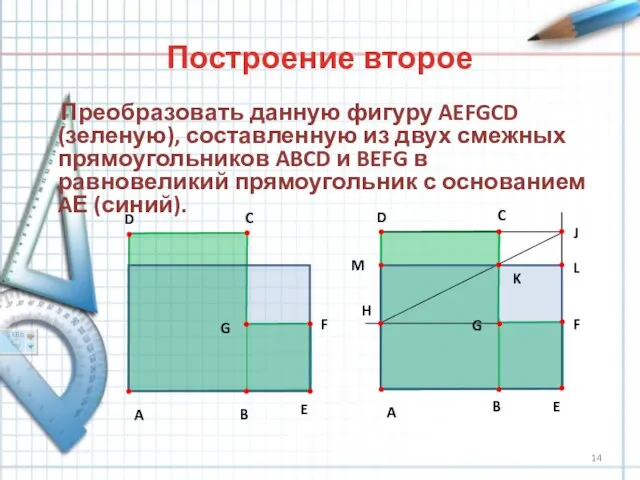
Построение второе
Преобразовать данную фигуру AEFGCD (зеленую), составленную из двух смежных прямоугольников ABCD и BEFG в равновеликий прямоугольник с основанием AЕ (синий).
A
E
F
G
C
D
A
E
F
G
C
D
H
J
K
B
M
L
B

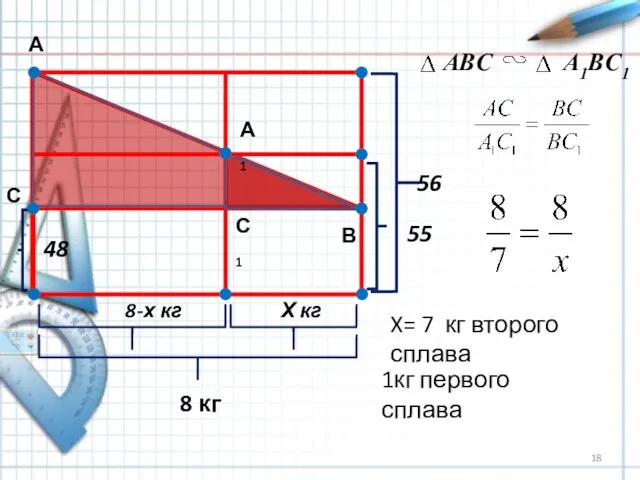
ТРИ СПЛАВА
Имеются два сплава золота и серебра; в одном количество этих металлов находится в отношении 2:3, в другом—в отношении 3:7. Сколько нужно взять каждого сплава, чтобы получить 8 кг нового сплава, в котором золото и серебро были бы в отношении 5:11?

Серебро составляет 3/5 первого сплава, 7/10 второго и 11/16 искомого.
Общий знаменатель этих дробей—80.
Следовательно, на каждые 80 частей в первом сплаве приходится 48 частей серебра, во втором—56, в искомом—55 частей.

48
8-х кг
Х кг
8 кг
55
56
А
В
С
А1
С1
ABC
A1BC1
X= 7 кг второго сплава
1кг первого сплава

Упражнение
Имеются два сплава золота и серебра; в одном количество этих металлов находится в отношении 1:2, в другом —в отношении 2:3. Сколько нужно взять каждого сплава, чтобы получить 44 кг нового сплава, в котором золото и серебро были бы в отношении 17:27?

Самостоятельная работа
II уровень
Прототип задания B12 (№ 99576)Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
I уровень
Прототип задания B12 (№ 99575) Имеется два сплава. Первый сплав содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?

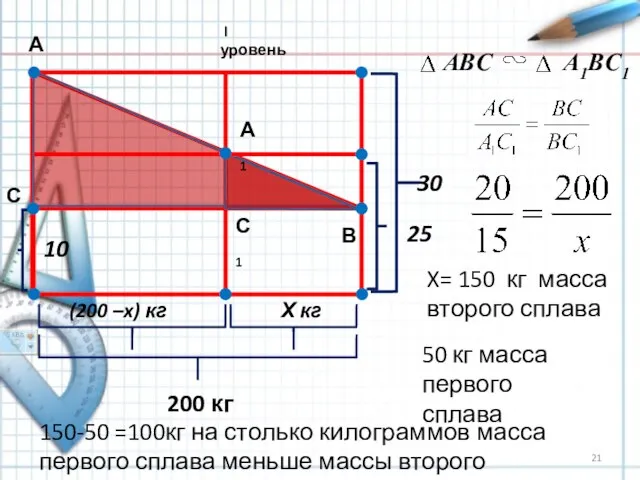
10
(200 –x) кг
Х кг
200 кг
25
30
А
В
С
А1
С1
ABC
A1BC1
X= 150 кг масса
второго сплава
50 кг масса
первого сплава
150-50 =100кг на столько килограммов масса первого сплава меньше массы второго
I уровень

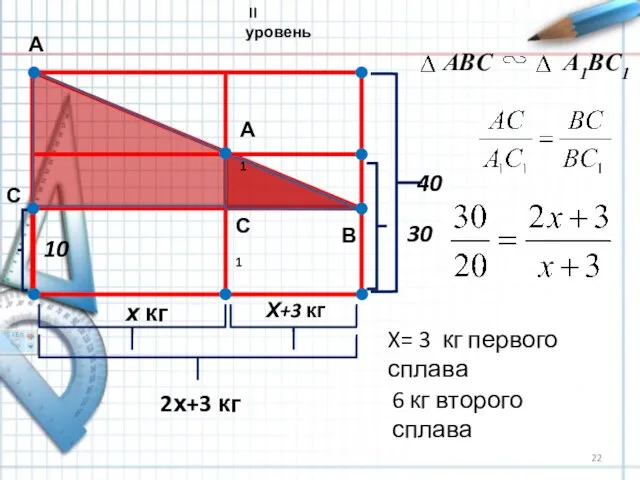
10
х кг
Х+3 кг
2х+3 кг
30
40
А
В
С
А1
С1
ABC
A1BC1
X= 3 кг первого сплава
6 кг второго сплава
II уровень

Что вы узнали нового?
Чему научились?
Что показалось особенно трудным?
Итог урока. Рефлексия