Содержание
- 2. /23 Литература Экономико-математические методы и прикладные модели: Учеб. пособие для вузов / Под ред. В.В. Федосеева.
- 3. /23 3.1. Принцип оптимальности в планировании и управлении Принцип оптимальности предполагает следующее: наличие определённых ресурсов наличие
- 4. /23 3.2. Задача линейного программирования Это развёрнутая форма записи Линейная целевая функция Линейные ограни-чения Условия неотрицательности
- 5. /23 3.2. Задача линейного программирования Это каноническая форма записи Линейная целевая функция Линейные ограни-чения Условия неотрицательности
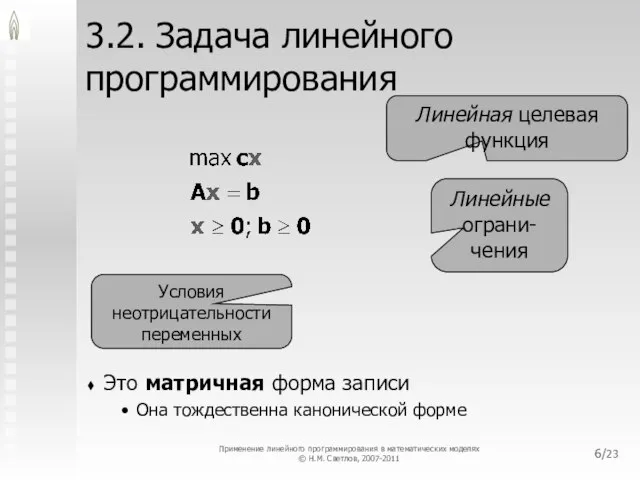
- 6. /23 3.2. Задача линейного программирования Это матричная форма записи Она тождественна канонической форме Линейная целевая функция
- 7. /23 3.2. Задача линейного программирования Это стандартная форма записи Линейная целевая функция Линейные ограни-чения Условия неотрицательности
- 8. /23 3.2. Любой вектор x, удовлетворяющий ограничениям и условиям неотрицательности (безотносительно к целевой функции), называется допустимым
- 9. /23 3.2. ЗЛП может: не иметь ни одного оптимального решения допустимой области не существует – система
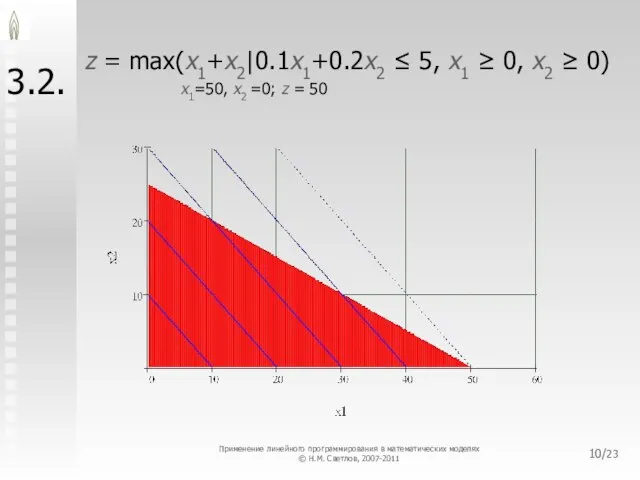
- 10. /23 3.2. z = max(x1+x2|0.1x1+0.2x2 ≤ 5, x1 ≥ 0, x2 ≥ 0) x1=50, x2 =0;
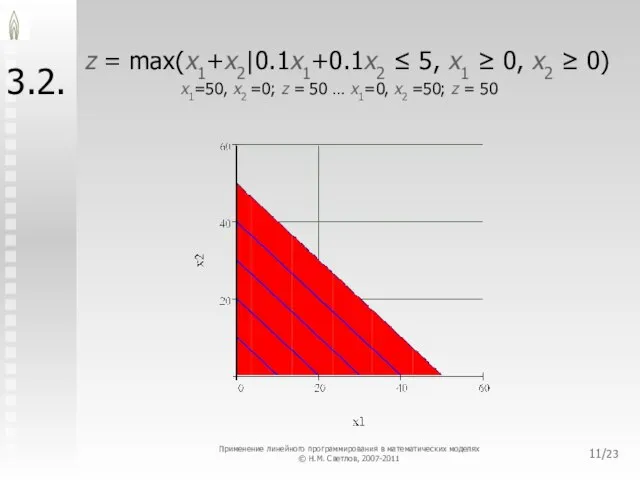
- 11. /23 3.2. z = max(x1+x2|0.1x1+0.1x2 ≤ 5, x1 ≥ 0, x2 ≥ 0) x1=50, x2 =0;
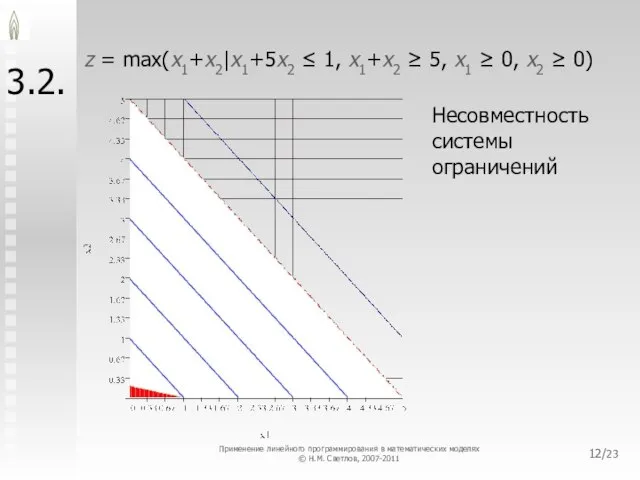
- 12. /23 3.2. z = max(x1+x2|x1+5x2 ≤ 1, x1+x2 ≥ 5, x1 ≥ 0, x2 ≥ 0)
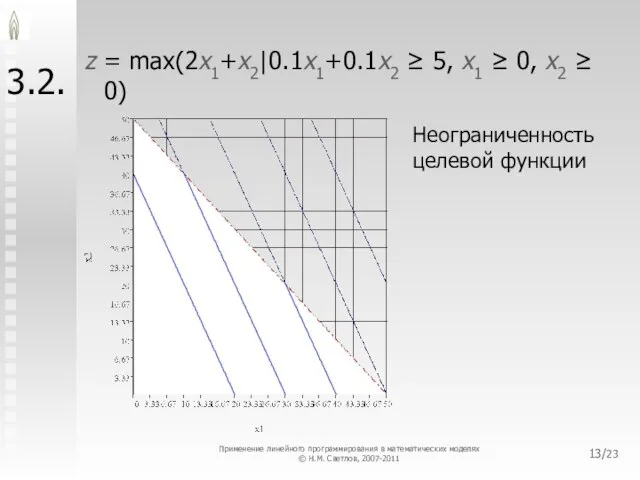
- 13. /23 3.2. z = max(2x1+x2|0.1x1+0.1x2 ≥ 5, x1 ≥ 0, x2 ≥ 0) Неограниченность целевой функции
- 14. /23 3.3. Симплексный метод Исходные условия применения симплексного метода ЗЛП записана в канонической форме Её ограничения
- 15. /23 3.3. z = max(x1+x2|0.1x1+0.2x2 ≤ 5, x1–2x2 ≤ 75, x1 ≥ 0, x2 ≥ 0)
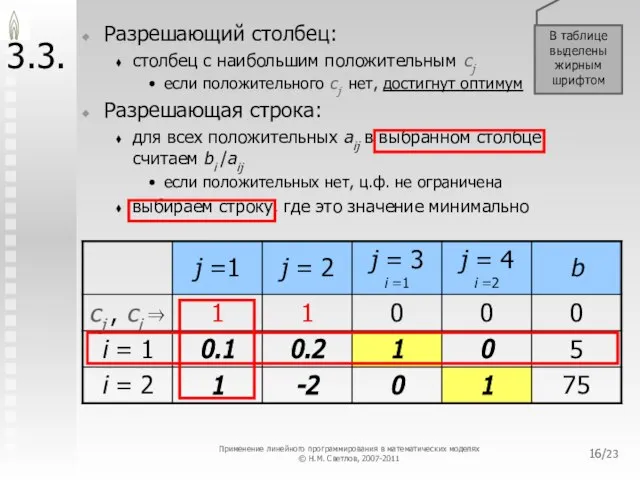
- 16. /23 В таблице выделены жирным шрифтом 3.3. Разрешающий столбец: столбец с наибольшим положительным cj если положительного
- 17. /23 3.3. Выполняем обыкновенные жордановы исключения во всей таблице: для строк i ≠i' : aijнов =
- 18. /23 3.3. Опорное решение может быть получено по следующей процедуре: Выбираем произвольный набор базисных переменных и
- 19. /23 3.3. В некоторых случаях алгоритм симплексного метода может зацикливаться. Пути преодоления этой проблемы описаны в
- 20. /23 3.4. Экономические приложения линейного программирования Матрица потребности в ресурсах для обеспечения единичного объёма производства в
- 21. /23 3.4. Экономические приложения линейного программирования Вектор цен продукции (за вычетом НДС), руб./ед. Вектор цен ресурсов
- 22. Применение линейного программирования в математических моделях (с) Н.М. Светлов, 2007 /23 3.5. Программное обеспечение линейного программирования
- 24. Скачать презентацию















 Контроллер «АКД-СК»
Контроллер «АКД-СК» III Красноярский экономический форум «Развитие востока страны»Круглый «Региональная политика России и региональные стратегии к
III Красноярский экономический форум «Развитие востока страны»Круглый «Региональная политика России и региональные стратегии к Государственный санитарно-эпидемиологический надзор в области гигиены питания
Государственный санитарно-эпидемиологический надзор в области гигиены питания Модель проектно-ориентированной системы управления
Модель проектно-ориентированной системы управления Совершенствование правового положения государственных и муниципальных учреждений: организационные, финансовые, правовые аспект
Совершенствование правового положения государственных и муниципальных учреждений: организационные, финансовые, правовые аспект Курская антоновка – символ Курской области
Курская антоновка – символ Курской области Памятка о ложных вызовах об актах терроризма
Памятка о ложных вызовах об актах терроризма Изделия из слоеного теста
Изделия из слоеного теста Презентация на тему Верблюд
Презентация на тему Верблюд  Мой народ – американцы
Мой народ – американцы Презентация на тему Сергей Есенин Юность
Презентация на тему Сергей Есенин Юность  Информационные технологии в жилищно-коммунальном хозяйстве Финляндии
Информационные технологии в жилищно-коммунальном хозяйстве Финляндии Презентация на тему готовимся к ГИА, В3, В6
Презентация на тему готовимся к ГИА, В3, В6  Жанр портрета в культуре разных времён
Жанр портрета в культуре разных времён История аниме
История аниме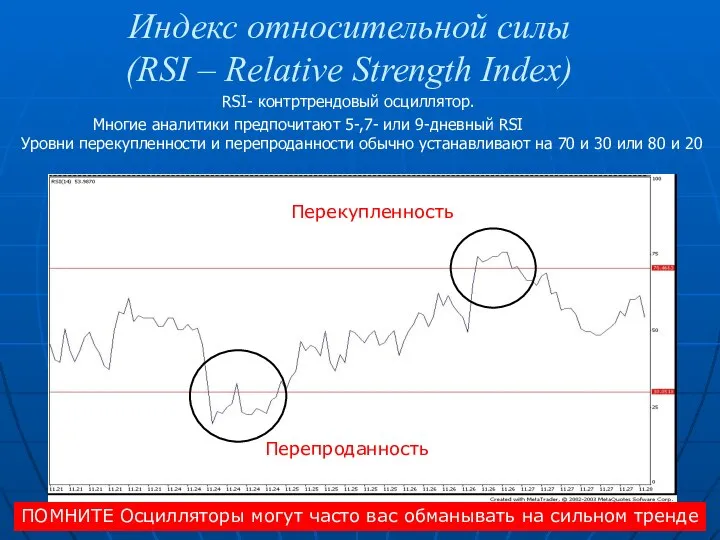 Индекс относительной силы
Индекс относительной силы Неживая и живая природа
Неживая и живая природа Реакторы, охлаждаемые водой сверхкритического давления при двухходовой схеме движения теплоносителя Ю.Д. Баранаев, А.П. Глебов, А.В
Реакторы, охлаждаемые водой сверхкритического давления при двухходовой схеме движения теплоносителя Ю.Д. Баранаев, А.П. Глебов, А.В speaking_club_yesno (2)
speaking_club_yesno (2) Мастер-класс Скрап-страницы моего лета
Мастер-класс Скрап-страницы моего лета Айларов Сослан Русланович
Айларов Сослан Русланович Елочные шарики из бумаги в технике квиллинг
Елочные шарики из бумаги в технике квиллинг Инновационная система и политика в РФ
Инновационная система и политика в РФ Семейный бюджет. Доходная и расходная части бюджета.
Семейный бюджет. Доходная и расходная части бюджета. Бухгалтерский учет, анализ и аудит
Бухгалтерский учет, анализ и аудит Праздник 1 мая
Праздник 1 мая мониторинг цен
мониторинг цен Анализ рынка детского питания на территории города Казани в одной из ключевых национальных сетей Пятерочка
Анализ рынка детского питания на территории города Казани в одной из ключевых национальных сетей Пятерочка