Применение методов компьютерной алгебры для решения задач планиметрии

АКТУАЛЬНОСТЬ
Алгоритмический метод проверки справедливости утверждений общего характера в евклидовой геометрии полезен в области искусственного интеллекта и геометрического моделирования, так как используется при создании программ проверки существования гипотетических связей между геометрическими объектами на плоскости.

ЦЕЛЬ И ЗАДАЧА РАБОТЫ
Цель– показать, как методы компьютерной алгебры могут помочь в доказательстве теорем планиметрии.
Задача - – изучить методы автоматического доказательтсва теорем и применить их на практике.

ПРЕДМЕТ ИЗУЧЕНИЯ
Предметом изучения является метод компьютерной алгребры автоматического доказательства теорем планиметрии.

ОСНОВА МЕТОДА
Условия и заключения геометрической теоремы задаются полиномиальными уравнениями от координат точек, о которых говорится в формулировке утверждения.
Примечание: Не всегда есть возможность это сделать.

ОСНОВА МЕТОДА
Геометрические утверждения, выводимые из предположений, представляются полиномами из идеала, порожденного предположениями

ОСНОВА МЕТОДА
Принадлежность полинома радикалу проверяется алгоритмически за конечное число шагов.

ПРИМЕНЕНИЕ РЕЗУЛЬТАТА ИССЛЕДОВАНИЯ НА ПРАКТИКЕ
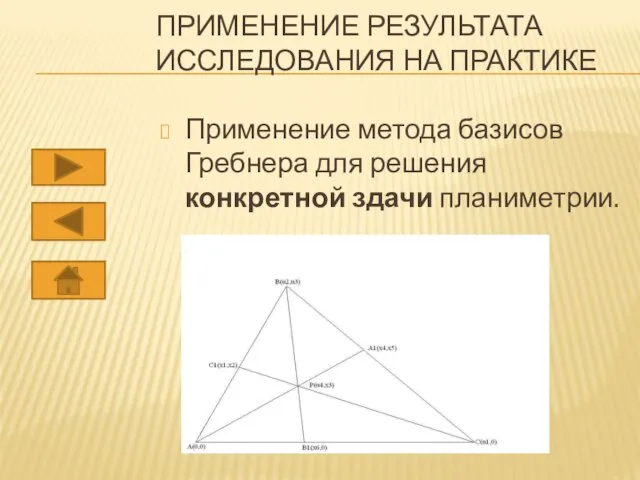
Применение метода базисов Гребнера для решения конкретной здачи планиметрии.

ПРИМЕНЕНИЕ РЕЗУЛЬТАТА ИССЛЕДОВАНИЯ НА ПРАКТИКЕ
Вычисления проводились в достаточно мощном пакете компьютерной алгебры Mathematica.

ЗАКЛЮЧЕНИЕ
Алгебраические многообразия в работе использованы для автоматического доказательства теоремы.
Такой же метод может быть использован для решения прямой и обратной задач робототехники для некоторых типов роботов.