Применение методов масштабируемого пространства в обработке сигналов

Основные требования к методам обработки сигналов на современном этапе развития вычислительных средств:
Возможность обработки нестационарных сигналов
Возможность обработки хаотических (фракталоподобных) сигналов
Возможность применения быстрых алгоритмов и удобство аппаратной реализации
Учет психофизиологических особенностей человеческого восприятия
Высокая адаптивность

Наиболее распространенные методы обработки сигналов:
Спектральные методы (Фурье-анализ и др. ортогональные преобразования)
Кратномасштабные методы (пирамидальные представления, Вейвлет-анализ)
Рекурсивно-фрактальные методы (системы итерируемых функций, анализ фрактальной динамики, марковские цепи и др.)
Комбинированные методы (динамическая модель дискретного пространства, адаптивная сегментация, масштабируемое пространство)

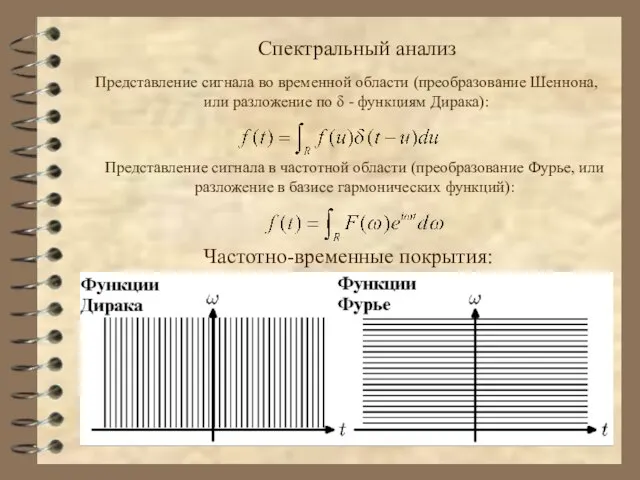
Спектральный анализ
Представление сигнала во временной области (преобразование Шеннона, или разложение по δ - функциям Дирака):
Представление сигнала в частотной области (преобразование Фурье, или разложение в базисе гармонических функций):
Частотно-временные покрытия:

Частотно-временная неопределённость
Спектральный анализ учитывает интегральные характеристики и удобен для анализа стационарных сигналов, в то время как для нестационарных сигналов необходима частотно-временная локализация особенностей
Нельзя найти функцию, локализующую событие в частотно-временной области с произвольно малой погрешностью (принцип неопределенности Гейзенберга):
(f – квадратично интегрируемая функция в с единичной нормой)
Неравенство Гейзенберга: для любой функции f(t) с единичной нормой и убывающей быстрее, чем t -1/2 при t→±∞, справедливо соотношение
F – преобразование Фурье функции f.

Функции, обеспечивающие частотно-временную локализацию с максимально возможной точностью -
модулированные гауссовы функции (фукнции Габора) вида
Способ частотно-временной локализации преобразования Фурье -
оконное преобразование Фурье
Окно w(t) – движущаяся по временной оси функция, имеющая компактный носитель, характеризующаяся частотой ω и сдвигом во времени τ.
Основные недостатки оконного преобразования Фурье - неоптимальная частотно-временная локализация и фиксированная ширина окна (неадаптивность обработки)
При
g(t) - функция Гаусса

Частотно-временное и масштабно-временное представления сигнала
Цель - устранение избыточности частотно-временных покрытий для представлений Фурье и Дирака
Частотно-временной подход - выбор временной протяженности функций независимо от частоты модуляции. Совпадает с оконным преобразованием Фурье:
, где
Масштабно-временной подход - ширина функций во времени обратно пропорциональна их частоте (ω0 Δ t = c):
, где

Покрытие частотно-временной плоскости
для частотно-временного (a) и масштабно-временного (b) представлений
В случае частотно-временного представления покрытие состоит из одинаковых прямоугольников, транслируемых по всей плоскости.
В случае масштабно-временного представления прямоугольники имеют одинаковую площадь, но их относительная разрешающая способность по частоте остается при этом неизменной
Масштабно-временное представление лежит в основе вейвлет-анализа сигналов

Вейвлет-анализ
Непрерывный
большая избыточность
низкая скорость
эффективен для анализа нестационарных сигналов
Дискретный
отсутствует избыточность
быстрые алгоритмы
эффективен для сжатия сигналов и изображений

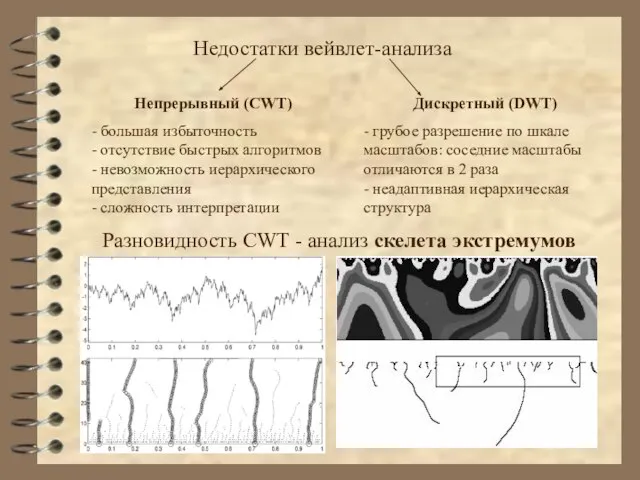
Недостатки вейвлет-анализа
Непрерывный (CWT)
- большая избыточность
- отсутствие быстрых алгоритмов
- невозможность иерархического представления
- сложность интерпретации
Дискретный (DWT)
- грубое разрешение по шкале масштабов: соседние масштабы отличаются в 2 раза
- неадаптивная иерархическая структура
Разновидность CWT - анализ скелета экстремумов

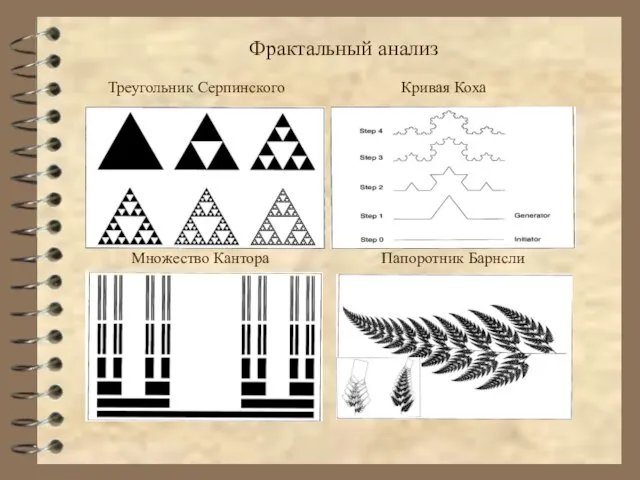
Фрактальный анализ
Треугольник Серпинского Кривая Коха
Множество Кантора Папоротник Барнсли

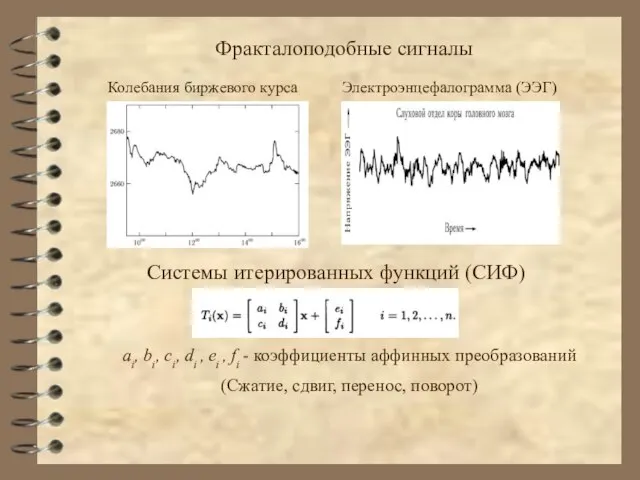
Фракталоподобные сигналы
Колебания биржевого курса Электроэнцефалограмма (ЭЭГ)
Системы итерированных функций (СИФ)
ai, bi, ci, di , ei , fi - коэффициенты аффинных преобразований
(Сжатие, сдвиг, перенос, поворот)

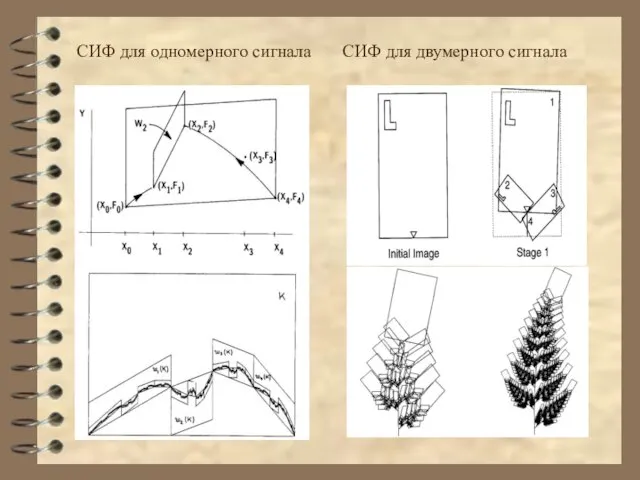
СИФ для одномерного сигнала СИФ для двумерного сигнала

Основные свойства представления сигналов
с помощью систем итерированных функций:
Достоинства:
Компактное рекурсивно-иерархическое представление
Сохранение деталей на любых масштабах
Качественное восстановление сигнала на любом масштабе
Эффективно в задачах сжатия сигналов и изображений, обладающих свойством самоподобия
Недостатки:
Высокая вычислительная сложность нахождения оптимальной СИФ
Сложность выбора эвристического алгоритма, адекватного природе сигнала (низкая адаптивность)

Анализ фрактальной размерности
Фрактальная размерность
, где ε - размер элемента покрытия фракталоподобного сигнала, N(ε) - число элементов покрытия
Способы вычисления фрактальной размерности:
Непосредственный или аналитический расчет. Низкая точность для дискретного представления сигнала
Косвенная оценка по характеристикам спектра мощности
Модель спектра мощности фракталоподобного сигнала:
Отсюда

Свойства оценки фрактальной размерности по спектру мощности с применением БПФ:
Достоинства:
Высокая скорость
Небольшое количество дискретных отсчетов, требуемых для оценки
Недостатки:
Низкая точность (большие флуктуации спектра мощности)
Несоответствие Фурье-спектра и обобощенного спектра (для ЭЭГ)
Несогласованность разложения в гармоническом базисе с фрактальной моделью сигнала

Теория масштабируемого пространства (МП)
Исходные предпосылки
Важные для нас свойства сигнала существуют только в определенном диапазоне масштабов. Если этот масштаб неизвестен, применение классических методов спектрального анализа, вычисляющих интегральные характеристики, не приносит ощутимых результатов.
При априорно неизвестном масштабе важных для нас особенностей сигнала наиболее эффективным является многомасштабное описание сигнала. Примеры: динамическая модель дискретного пространства, методы кратномасштабного и вейвлет-анализа.
Окончательной целью многомасштабного описания является построение иерархии особенностей сигнала на основе анализа взаимосвязи этих особенностей на различных масштабах. Взаимосвязь между свойствами сигнала на различных масштабах желательно определить адаптивно, т.е. структурное представление должно определяться в первую очередь свойствами самого сигнала.

Концепция масштабируемого пространства.
Аксиоматика
— максимально возможное количество элементарных объектов или особенностей, доступных для восприятия человека, конечно и определяется разрешающей способностью соответствующего органа восприятия;
— при огрублении масштаба восприятия элементарные объекты сливаются, объединяясь в объекты более высокого уровня иерархии. Подобное правило справедливо для любых объектов вплоть до самого грубого масштаба восприятия. Количество объектов при огрублении уровня восприятия монотонно убывает, при этом возникновение новых объектов или особенностей, не являющихся объектами предыдущего уровня иерархии, недопустимо (аксиома причинности);
— закон объединения объектов в иерархическую структуру не зависит ни от пространственного направления, ни от масштаба уровня иерархии (аксиома изотропности);

Концепция масштабируемого пространства.
Аксиоматика (продолжение)
— Желательно, чтобы данная иерархия обладала свойством инвариантности относительно временного сдвига и изменения амплитуды исходного сигнала (принцип линейности);
— Желательно, чтобы любой уровень иерархии можно было получить не только из исходного сигнала, но и из любого другого уровня иерархии с большей степенью детализации (свойство полугруппы).
Типичная функция апертуры регистрирующего элемента (сканер, фотоаппарат и т.п.)
Регистрация большинства физических процессов по сути своей есть восстановление сигнала на некотором уровне линейного масштабируемого пространства

Концепция масштабируемого пространства.
Определение.
Масштабируемое пространство (МП) является оригинальным способом адаптивного иерархически структурированного многомасштабного описания сигнала.
По сути своей построение МП представляет собой операцию разложения исходного сигнала f : Rn → R в семейство { Tt f | t ≥ 0 } постепенно сглаживаемых, упрощающихся версий сигнала, удовлетворяющих вышеуказанным требованиям (аксиомам).
Исторически самым первым и наиболее исследованным МП является гауссовское МП, для которого
где Kσ - функция Гаусса со стандартным отклонением σ
Доказано, что Гауссово МП - единственное непрерывное линейное МП, удовлетворяющее всем вышеуказанным требованиям (аксиомам)

Линейное гауссово масштабируемое пространство
В одномерном случае построение гауссова МП определяется преобразованием интегрального типа
удовлетворяющее следующим 5 аксиомам:
– Линейность(в отношении умножения):
– Инвариантность к сдвигу:
– Масштабная инвариантность:
– Свойство полугруппы:
– Свойство положительности:
Доказано, что единственным преобразованием, удовлетворяющим всем этим аксиомам, является свертка с гауссианом вида

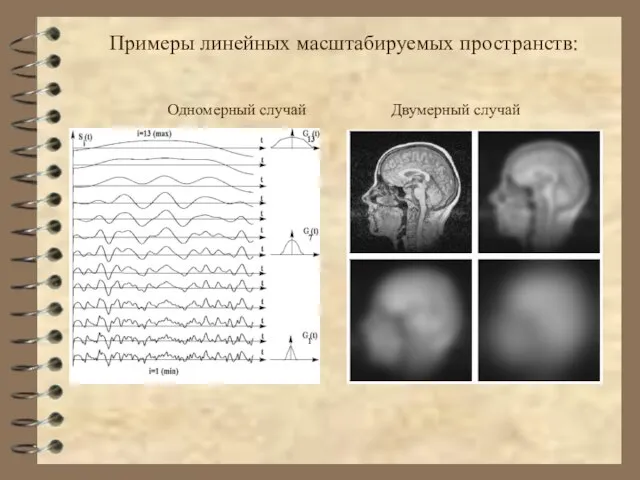
Примеры линейных масштабируемых пространств:
Одномерный случай Двумерный случай

Физический смысл масштабируемого пространства (МП)
Процесс диффузии:
Уравновешивание разности концентраций при сохранении массы
Закон Фика:
j=-D∇u (Градиент концентрации ∇u создает поток j,
D-диффузионная матрица, в изотропном случае – скалярный коэффициент рассеяния, j параллелен ∇u)
Уравнение непрерывности (сохранение массы):
∂ u/∂ t=-div j
Уравнение диффузии:
∂ u/∂ t =div(D∇u)
Для изотропного случая решение уравнения диффузии совпадает с разложением сигнала в линейном гауссовом МП

Биологические и физиологические истоки масштабируемого пространства
Система зрения человека способна к обнаружению и идентификации нескольких объектов различных размеров одновременно (многомасштабность). Многомасштабной является также система тактильного восприятия.
Гауссовская фильтрация лежит в основе первичной модели человеческого зрения (early vision). Физиологические модели, описывающие область восприятия в сетчатке глаза, используют функцию Гаусса в качестве масштабирующего фильтра.
Лапласеан гауссиана (Вейвлет «Мексиканская шляпа»), используется в модели профиля чувствительности области, окружающей центр поля восприятия.
На стадии идентификации начинают превалировать рекурсивные методы восприятия, характеризующиеся глубокой обратной связью глаз-мозг, что подразумевает использование структурного представления изображения

История развития теории масштабируемого пространства (МП)
Иидзима (Iijima), 1962 - первая попытка аксиоматизации МП
Уиткин (Witkin), 1983 - первая англоязычная публикация, начало широкого развития теории
Кёндеринк (Koenderink), 1984 - популяризация концепции МП в области машинного зрения, ее связь с особенностями человеческого восприятия
Бобод и др. (Babaud et al.), 1986 - доказательство принципа причинности для одномерного линейного гауссова МП
Йохансен (Johansen), 1986 - доказательство аналога теоремы Котельникова-Шеннона для вершинных точек МП

История развития теории МП (продолжение)
Малик, Перона (Malik, Perona), 1990 - теория нелинейного анизотропного МП
Линдеберг (Lindeberg), 1990 -дискретное представление линейного МП
Джеквэй (Jackway), 1992 - дискретное МП на основе операций математической морфологии
Ванг, Ли (Wang, Lee), 1998 - линейное МП на основе B-сплайнов
Йохансен (Johansen), 2000 - метод полиномиального восстановления одномерного сигнала по вершинным точкам МП

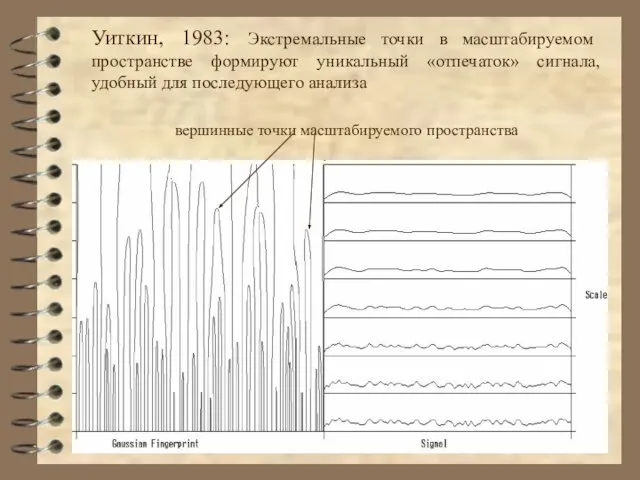
Уиткин, 1983: Экстремальные точки в масштабируемом пространстве формируют уникальный «отпечаток» сигнала, удобный для последующего анализа
вершинные точки масштабируемого пространства

Йохансен, 1986 (аналог теоремы Котельникова-Шеннона для МП):
Одномерный сигнал с ограниченной полосой пропускания единственным образом с точностью до постоянного множителя и смещения по шкале амплитуд может быть определен по вершинным точкам МП
Поскольку количество вершинных точек сигнала равно половине количества локальных экстремумов N, для однозначного восстановления сигнала достаточно запоминать значения N/2 временных и N/2 масштабных координат вершинных точек
2000 - алгоритм полиномиального восстановления сигнала по вершинным точкам

Джеквэй, 1992: открытие непрерывного и дискретного морфологического МП, удовлетворяющего аксиомам нелинейного МП
Основные операции математической морфологии:
- расширение
- сужение
- открытие (расширение+сужение)
- закрытие (сужение+расширение)
Пример морфологической обработки одномерного сигнала:

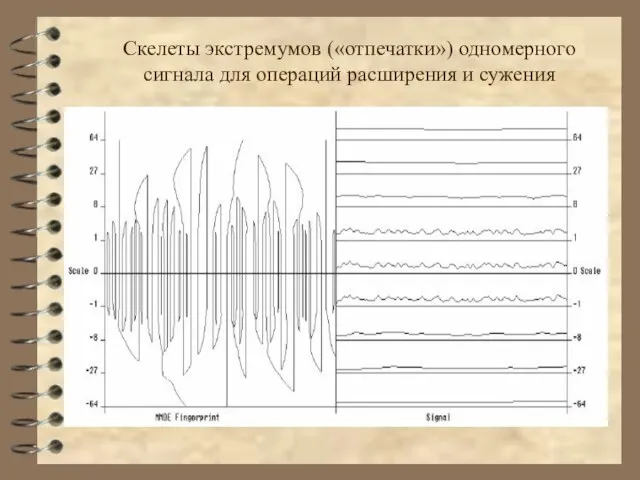
Скелеты экстремумов («отпечатки») одномерного сигнала для операций расширения и сужения

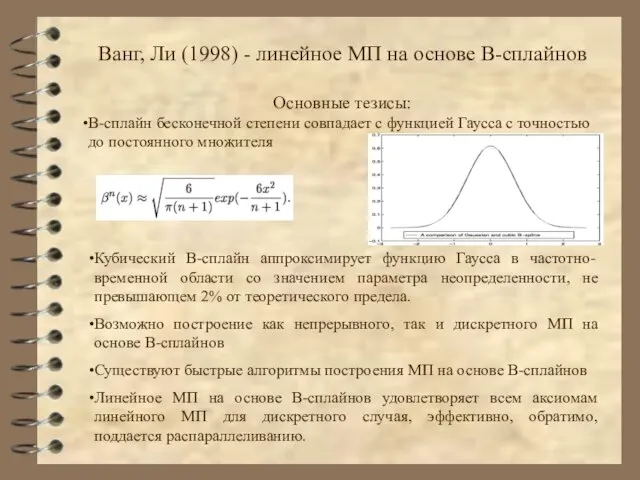
Ванг, Ли (1998) - линейное МП на основе B-сплайнов
Основные тезисы:
B-сплайн бесконечной степени совпадает с функцией Гаусса с точностью до постоянного множителя
Кубический B-сплайн аппроксимирует функцию Гаусса в частотно-временной области со значением параметра неопределенности, не превышающем 2% от теоретического предела.
Возможно построение как непрерывного, так и дискретного МП на основе B-сплайнов
Существуют быстрые алгоритмы построения МП на основе B-сплайнов
Линейное МП на основе B-сплайнов удовлетворяет всем аксиомам линейного МП для дискретного случая, эффективно, обратимо, поддается распараллеливанию.

Целью работы является разработка теоретических основ адаптивного рекурсивно-иерархического представления произвольных непрерывных одномерных сигналов, их обобщение на дискретные и многомерные сигналы конечной длины и разработка на основании полученных результатов прототипа программной системы компрессирования, сегментации и анализа параметров фракталоподобных сигналов на основе решения проблемы идентификации семантически структурированных областей этих сигналов с использованием методов масштабируемого пространства и рекурсивно-фрактальных методов представления сигнала.

Общая задача работы сводится к построению адекватной математической модели представления фракталоподобных сигналов на основе общей теории непрерывных сигналов, обеспечивающей комплексное решение проблемы выделения уровней признаков, элементов этих уровней, их интерполяцию и экстраполяцию на основе рекурсивных межуровневых связей. Решение данных задач обеспечивается решением следующих конкретных задач:
1) Разработка методов многоуровневой сегментации одномерных сигналов для адаптивного выделения различных областей и их идентификации.
2) Разработка адаптивно-динамической структуры данных, обеспечивающей эффективное описание и объединение связных областей.
3) Построение системы структурного анализа локальных областей исследуемого сигнала на основе масштабного изменения признаков, обеспечивающей масштабно-инвариантное представление сигнала.
4) Разработка механизма идентификации локальных областей по масштабно-независимому повторению признаков.
5) Разработка методов межуровневой и внутриуровневой аппроксимации сигналов.
6) Экспериментальное обоснование разработанных решений на основе компактной программной реализации данной системы.

Научная новизна. В процессе решения поставленных задач получены следующие новые научные результаты:
1) Многоуровневая модель выделения областей одномерных сигналов, включающая:
- формализованное описание многоуровневой иерархической структуры для непрерывных и дискретных сигналов неизвестной природы.
- метод порождения системы рекурсивно вложенных подпространств посредством свертки со сглаживающими масштабируемыми функциями, полученными на основе теории масштабируемого пространства;
- методы итерационной детализации сигнала по областям
ненулевых значений сигнала и его производных, сводящиеся к разделению и объединению смежных областей на основе методов двоичного поиска.
2) Рекурсивно-динамическая структура данных, в которых многомерное разбиение строится в виде n-арных деревьев, преобразуемых в ориентированный граф с рекурсивно формируемыми структурными связями на основе аффинных и циклических преобразований подобия.

Практическая ценность работы. Практическая ценность предложенной модели рекурсивно-иерархического представления сигналов охватывает широкий спектр задач. Она может использоваться в системах передачи, компрессии, распознавания и реставрации данных, то есть охватывает практически весь спектр методов обработки сигналов. Возможность применения быстрых алгоритмов кодирования разработанной структуры данных и восстановления сигнала, а также простота аппаратной реализации допускают применение разработанных методов в реальном времени.
Разработанные и проверенные на опыте структуры данных позволяют проектировать и реализовывать программные системы обработки сигналов любого происхождения, однако наилучшие результаты достигаются на нестационарных фракталоподобных сигналах.
Резкое сокращение времени поиска при реализации рекурсивно- фрактального представления обеспечивает эффективное решение проблемы выбора близкого к оптимальному решения в условиях ограниченных ресурсов памяти и быстродействия. Адаптивность предложенной модели обеспечивает интерактивный контроль со стороны пользователя,
обеспечивающий оптимальное соотношение коэффициента сжатия и качества восстановления сигнала.

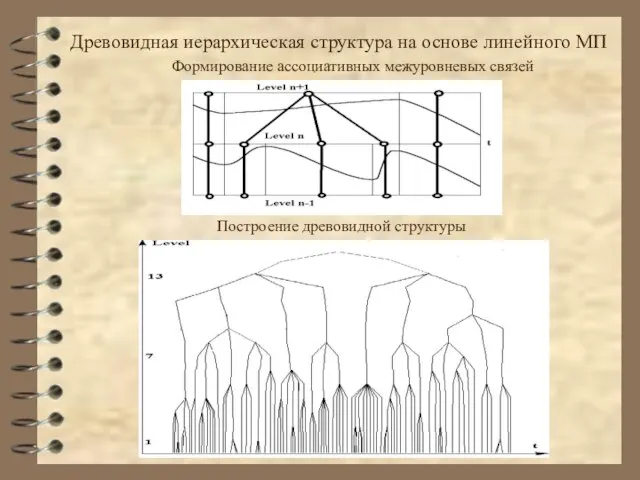
Древовидная иерархическая структура на основе линейного МП
Формирование ассоциативных межуровневых связей
Построение древовидной структуры

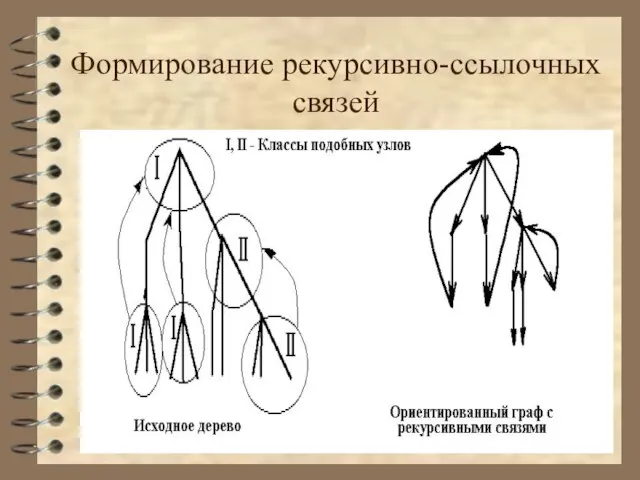
Формирование рекурсивно-ссылочных связей

Особенности формирования рекурсивно-иерархической структуры:
Точные значения уровней дробления древовидной структуры (вершинных точек) по шкале времени и масштаба находятся методом двоичного поиска
Древовидная структура обеспечивает масштабную инвариантность восстановления сигнала по протяженности и амплитуде
Поиск подобия разномасштабных узлов древовидной структуры аналогичен поиску в методе фрактального кодирования, однако ведется на сокращенном наборе данных, имеющих осмысленную интерпретацию
Все не имеющие потомков узлы структуры выражаются через узлы более грубых уровней иерархии по критерию минимума СКО. Таким образом формируется рекурсивно-ссылочная структура бесконечной глубины детализации на конечном наборе данных, подобная фрактальной СИФ.
Восстановление сигнала из структуры на произвольном уровне производится методом сплайн-интерполяции

Основные возможности программы Scale-Space
- Запись с микрофона и воспроизведение звука;
- Работа с моно- и стерео-файлами формата WAV PCM;
- Графическое отображение древовидной структуры;
- Восстановление сигнала на необходимом уровне масштабирования, вычисление СКО;
- Запись структурированного представления в файл;
- Возможность звукового воспроизведения сигнала в структурированном представлении.

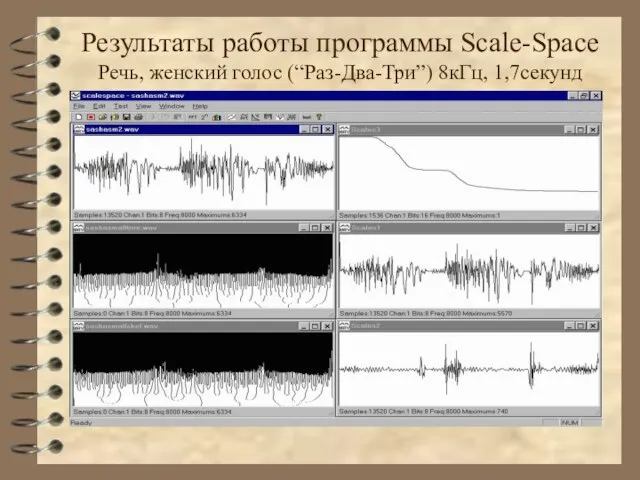
Результаты работы программы Scale-Space
Речь, женский голос (“Раз-Два-Три”) 8кГц, 1,7секунд

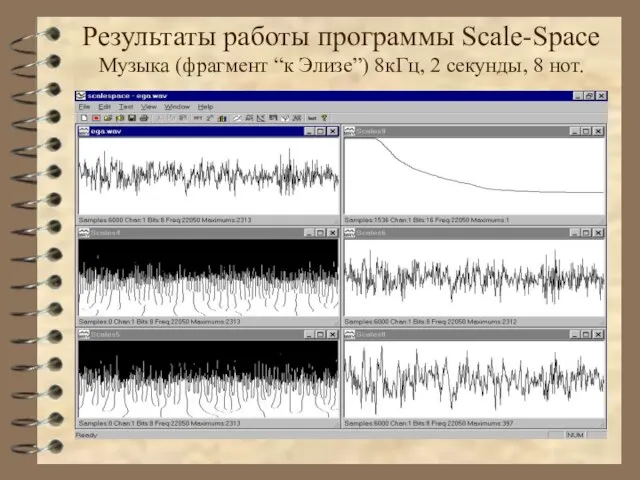
Результаты работы программы Scale-Space
Музыка (фрагмент “к Элизе”) 8кГц, 2 секунды, 8 нот.

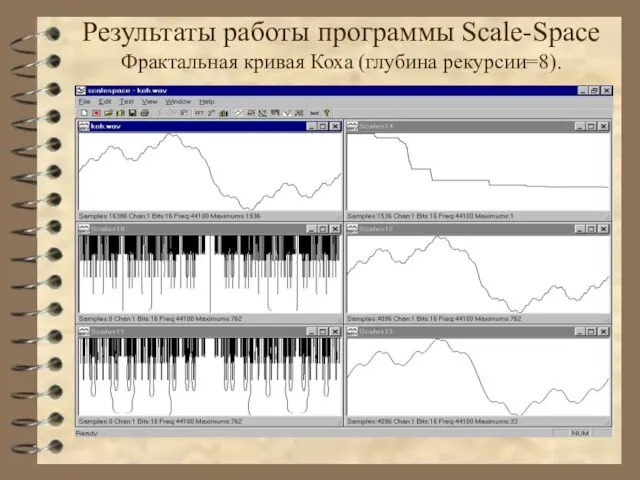
Результаты работы программы Scale-Space
Фрактальная кривая Коха (глубина рекурсии=8).

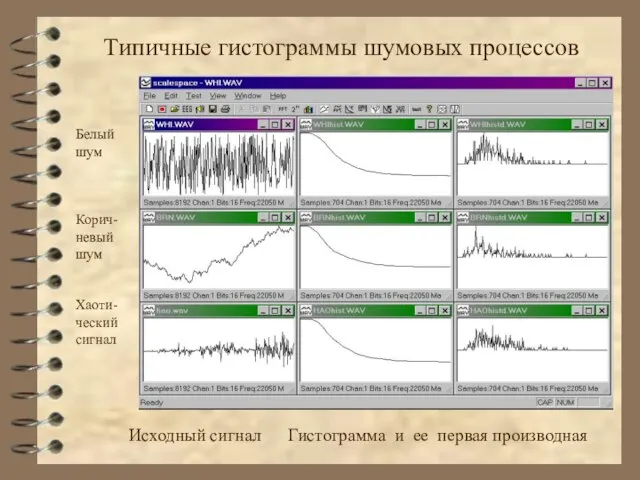
Типичные гистограммы шумовых процессов
Белый шум
Корич-невый шум
Хаоти-ческий сигнал
Исходный сигнал Гистограмма и ее первая производная

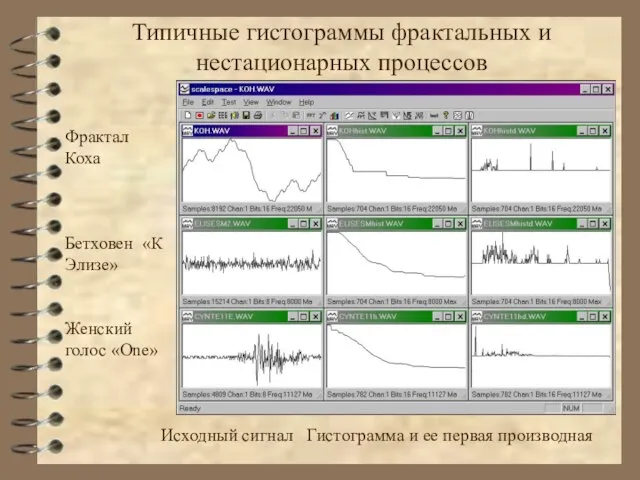
Типичные гистограммы фрактальных и нестационарных процессов
Фрактал Коха
Бетховен «К Элизе»
Женский голос «One»
Исходный сигнал Гистограмма и ее первая производная

Определение фрактальной размерности на основе МП
сглаживание в линейном гауссовом МП хорошо аппроксимирует фрактальную структуру сигнала: число экстремумов приближенно равно числу кусочно-линейных элементов на данном уровне рекурсии
суммарная длина кусочно-линейных элементов на данном уровне рекурсии пропорциональна среднему абсолютному значению первой производной на данном уровне; величина производной в свою очередь пропорциональна скорости монотонного убывания экстремумов при сглаживании в МП
для определения фрактальной размерности сигнала достаточно отследить его поведение при сглаживании в МП со шкалой масштабов, линеаризованной по среднему значению модуля первой производной
преимуществами данного метода являются легкость интерпретации и более гладкий (монотонно убывающий) характер анализируемой кривой, что влечет большую точность вычислений при одинаковом количестве исходных данных.

Основные результаты работы состоят в следующем:
1) На основе обобщения понятия области сигнала разработана многоуровневая модель представления одномерных сигналов, обеспечивающая восстановление приближения исходного сигнала на любом уровне иерархии.
2) Для оптимизации представления дискретных сигналов в рамках данной модели разработана динамическая структура данных, в которой многоуровневое представление сигнала задается в виде неравновесного дерева постоянной -арности с индексированными связями, обладающее временной и апмлитудной инвариантностью представления.
3) В рамках структуры данных для улучшения качества декомпрессии и реставрации сигнала предложен способ рекурсивного представления элементов нижнего уровня структуры через элементы более высокого иерархического уровня на основе набора циклических и аффинных преобразований.
4) Разработан программный комплекс, обеспечивающий применение разработанной модели и структуры данных в широкой области задач обработки сигналов.