четных и нечетных функцийИз пунктов Четные и нечетные функции,Построение графиков четных и нечетных функций и Периодические функции, что построение графика функции лучше начинать с ее исследования, которое состоит в том, что для данной функции:
1) находят ее область определения;
2) выясняют, является ли функция f четной или нечетной, является ли периодической.
Далее находят: 3) точки пересечения графика с осями координат;
4) промежутки знакопостоянства;
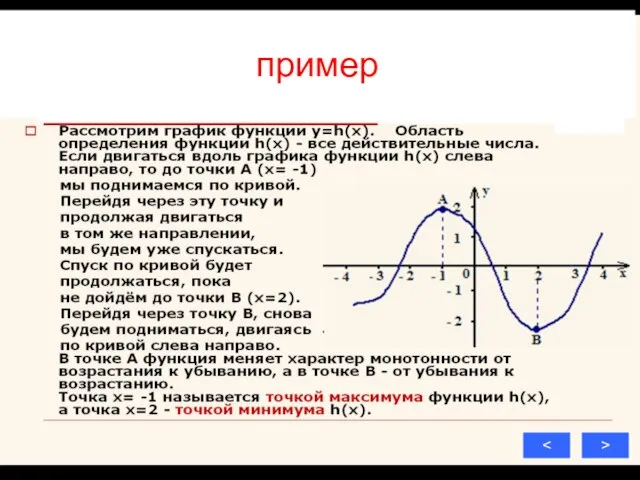
5) промежутки возрастания и убывания;
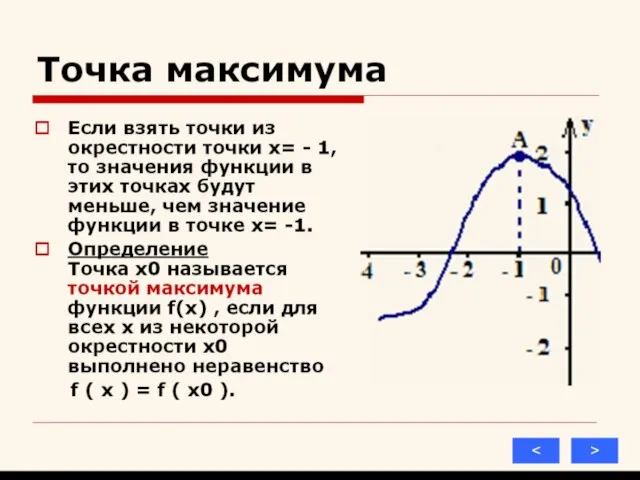
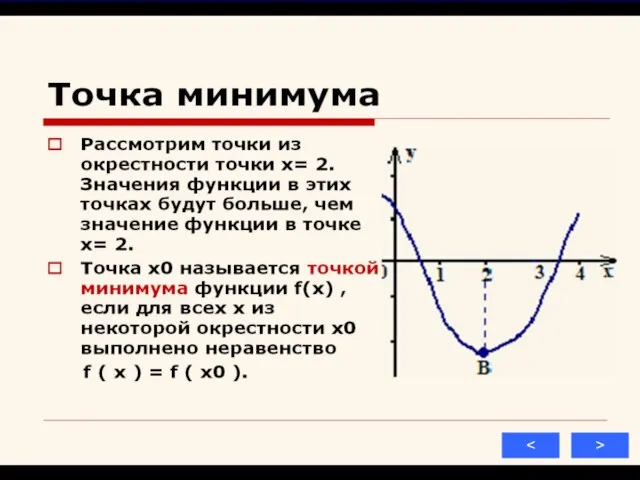
6) точки экстремума и значения f в этих точках
и 7) исследуют поведение функции в окрестности «особых» точек и при больших по модулю х.
На основании такого исследования строится график функции.
Исследование функции на возрастание (убывание) и на экстремум удобно проводить с помощью производной. Для этого сначала находят производную функции f и ее критические точки, а затем выясняют, какие из них являются точками экстремума.
Примеры применения производной к исследованию функций
>
<







 Характеристика внеурочных форм занятий: гимнастика до занятий, физкультминутки, динамичные перемены, спортивный час
Характеристика внеурочных форм занятий: гимнастика до занятий, физкультминутки, динамичные перемены, спортивный час Бабочки 7 класс
Бабочки 7 класс Никотиновый, алкогольный и наркотический геноцид
Никотиновый, алкогольный и наркотический геноцид Программно - аппаратный комплекс измерения RMS значений полной и активной мощности на платформе STM 32
Программно - аппаратный комплекс измерения RMS значений полной и активной мощности на платформе STM 32 1(16)
1(16) Глобальные проблемы человечества
Глобальные проблемы человечества Метод урахування невизначеності при вимірюванні/класифікації властивостей об’єктів за показниками якості
Метод урахування невизначеності при вимірюванні/класифікації властивостей об’єктів за показниками якості Создание авторской коллекции
Создание авторской коллекции Средства формирования физической культуры личности
Средства формирования физической культуры личности Чертежи соединений деталей
Чертежи соединений деталей Всероссийская олимпиада по физике
Всероссийская олимпиада по физике Сжимать иль не сжимать – вот в чем вопрос
Сжимать иль не сжимать – вот в чем вопрос Коррекционно-развивающее занятие
Коррекционно-развивающее занятие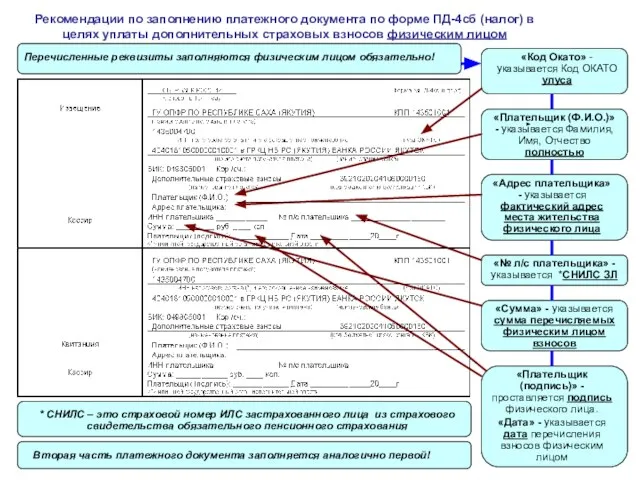 Рекомендации по заполнению платежного документа по форме ПД-4сб (налог) в целях уплаты дополнительных страховых взносов физически
Рекомендации по заполнению платежного документа по форме ПД-4сб (налог) в целях уплаты дополнительных страховых взносов физически Машины постоянного тока. Назначение и области применения МПТ
Машины постоянного тока. Назначение и области применения МПТ Презентация на тему День Ивана Купалы
Презентация на тему День Ивана Купалы  Индивидуально для бестолочь
Индивидуально для бестолочь Юрий Алексеевич Гагарин
Юрий Алексеевич Гагарин Презентация_ заполнить (строго 1 страница!) (1)
Презентация_ заполнить (строго 1 страница!) (1) Хозяйство России. Обобщение и коррекция знаний
Хозяйство России. Обобщение и коррекция знаний И Н Т Е Р В Е Н Ц И Яили о здоровье физическом и духовном
И Н Т Е Р В Е Н Ц И Яили о здоровье физическом и духовном МИМ № 22«Лунный месяц»
МИМ № 22«Лунный месяц» Презентация на тему Правописание сочетаний Чк чн
Презентация на тему Правописание сочетаний Чк чн Беспроводная передача энергии
Беспроводная передача энергии Travelling and Transport
Travelling and Transport Ориентирование
Ориентирование АЛГЕБРА ЛОГИКИ
АЛГЕБРА ЛОГИКИ Пропедевтический курс краеведения в начальной школе «Мой родной край»
Пропедевтический курс краеведения в начальной школе «Мой родной край»