Содержание
- 3. де де
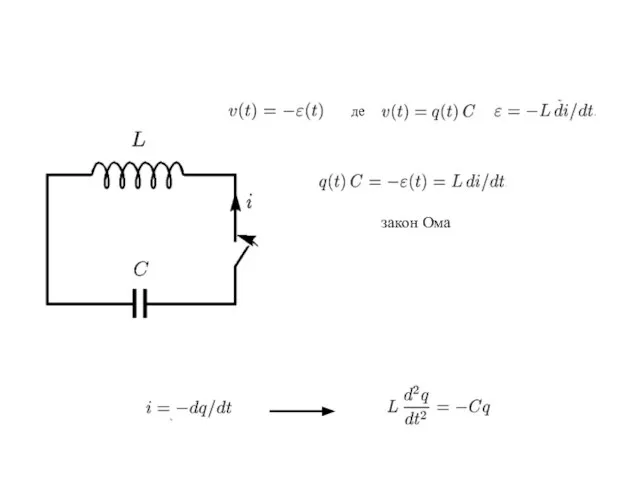
- 4. де закон Ома
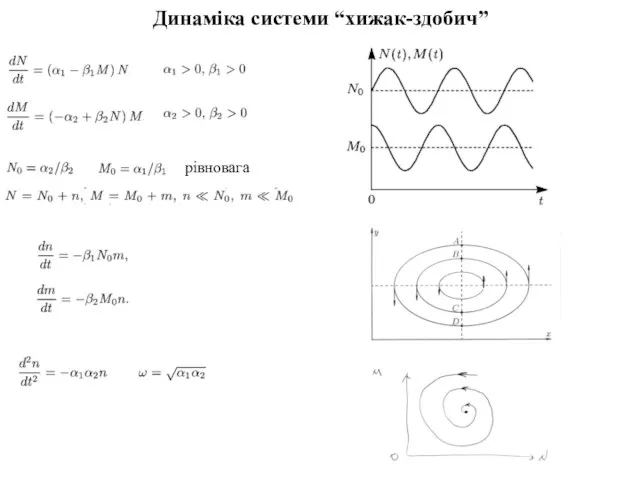
- 5. Динаміка системи “хижак-здобич” рівновага
- 6. Динаміка зайнятості заробітна плата чисельність зайнятих число робітників (зарплата) змінюється пропорційно змінам зарплати (числу робітників) відносно
- 7. Принцип ієрархії моделей
- 8. Закон збереження імпульсу імпульс ракети імпульс, що переданий газом мах початкова маса корисна маса структурна маса
- 9. Ієрархія моделей структурна маса ракети маса палива початкова маса ракети при (1) (2) (3)
- 10. Ієрархія моделей (модель Всесвіту) Edwin Hubble 1889-1953 Vesto Slipher 1875-1969 William Huggins 1824-1910 Willem de Sitter
- 11. Ієрархія моделей (модель Всесвіту) (a) (б) або А. А. Фридман 1916
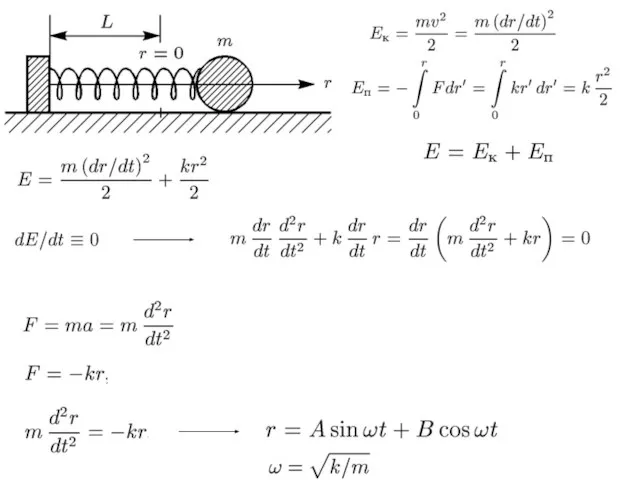
- 12. Популяційна динаміка
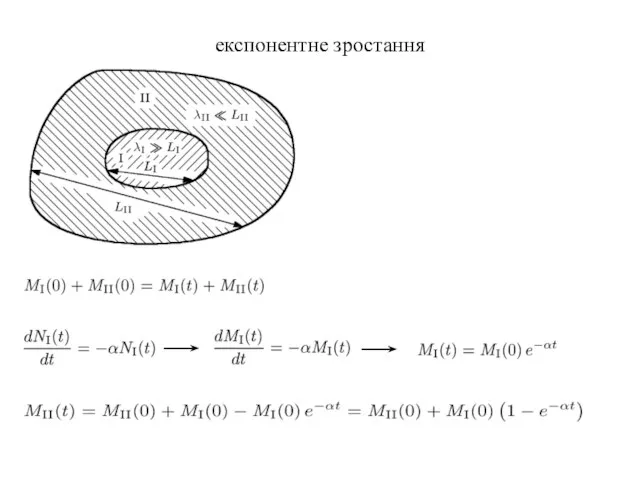
- 13. експонентне зростання
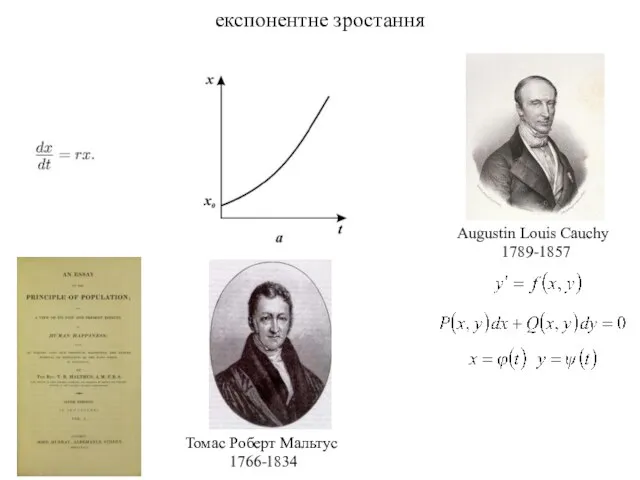
- 14. експонентне зростання Томас Роберт Мальтус 1766-1834 Augustin Louis Cauchy 1789-1857
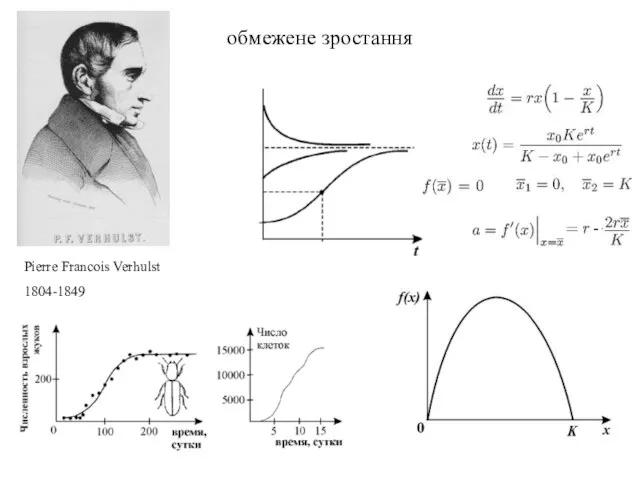
- 15. обмежене зростання Pierre Francois Verhulst 1804-1849
- 16. Дослідження стійкості стаціонарного стану з урахуванням та або де де - довільна стала
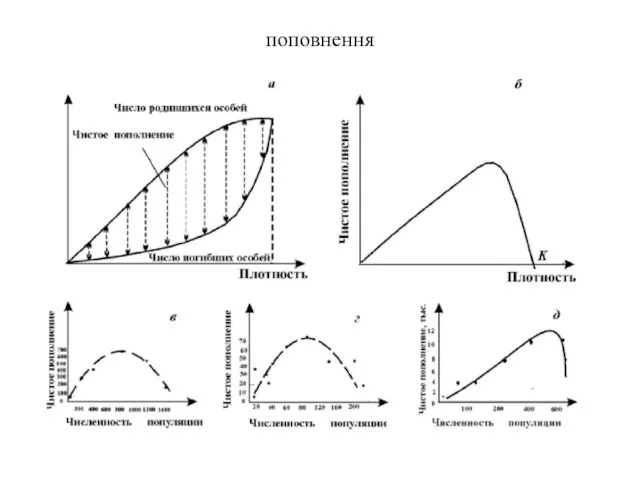
- 17. поповнення
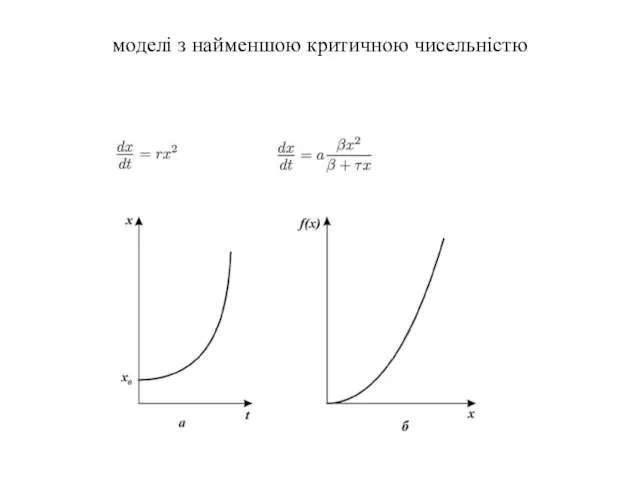
- 18. моделі з найменшою критичною чисельністю
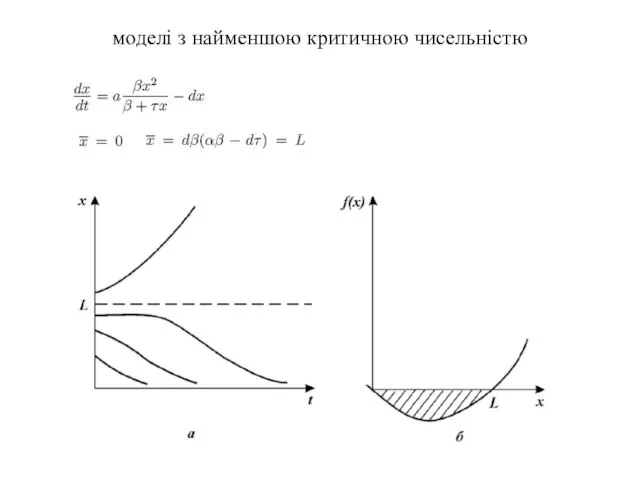
- 19. моделі з найменшою критичною чисельністю
- 21. Скачать презентацию








 «Настольная кукла»
«Настольная кукла» Форматы графических файлов
Форматы графических файлов Pets and presidents
Pets and presidents Елена Александровна Благинина
Елена Александровна Благинина Легкая атлетика. Определение лёгкой атлетики
Легкая атлетика. Определение лёгкой атлетики Основные требования к кандидатской диссертацииКак написать хорошую диссертацию
Основные требования к кандидатской диссертацииКак написать хорошую диссертацию Презентация на тему Наполеон и Кутузов по Толстому
Презентация на тему Наполеон и Кутузов по Толстому Начертательная геометрия
Начертательная геометрия Межличностные отношения
Межличностные отношения Затратный подход. Метод оценки стоимости объекта с учётом износа
Затратный подход. Метод оценки стоимости объекта с учётом износа Имя числительное (3 класс)
Имя числительное (3 класс) «1С-Отчетность»удобный способэлектронной отчетности
«1С-Отчетность»удобный способэлектронной отчетности Электронная коммерция в туризме
Электронная коммерция в туризме Тундра 3 класс
Тундра 3 класс Многие песни А. Пахмутовой незаметно вошли в нашу жизнь, они активно воздействуют на людей- воспитывают их мысли и чувства, помогаю
Многие песни А. Пахмутовой незаметно вошли в нашу жизнь, они активно воздействуют на людей- воспитывают их мысли и чувства, помогаю Моя республикаТатарстан
Моя республикаТатарстан Понятие, предмет, объект, субъект, история развития муниципального права
Понятие, предмет, объект, субъект, история развития муниципального права Государственная программа "Образование и развитие инновационной экономики: внедрение современной модели образования в 2009 - 2012 г
Государственная программа "Образование и развитие инновационной экономики: внедрение современной модели образования в 2009 - 2012 г Мой любимый детский сад Журавушка
Мой любимый детский сад Журавушка Олимпийский центр «Вентспилс»
Олимпийский центр «Вентспилс» Использование результатов ОГЭ и ЕГЭ в повышении качества образования по иностранному языку
Использование результатов ОГЭ и ЕГЭ в повышении качества образования по иностранному языку Молодіжні субкультури
Молодіжні субкультури УЧИТЕЛЯ
УЧИТЕЛЯ Презентация на тему Продажа имения старой графини» математическая игра для10-11 классов
Презентация на тему Продажа имения старой графини» математическая игра для10-11 классов  Что в имени тебе моем...?
Что в имени тебе моем...? dr
dr Мастер-класс по изготовлению куклы-дергунчика
Мастер-класс по изготовлению куклы-дергунчика Водоросли
Водоросли