Содержание
- 2. Наш проект - учебный, практического применения. В школьном туре олимпиады встретилась задача. Мы решили изучить подробнее
- 3. Дирихле родился в вестфальском городе Дюрене в семье почтмейстера. В 12 лет Дирихле начал учиться в
- 4. - В 1827г. устраивается на должность приватдоцента университета Бреслау (Вроцлав). - В 1829 г. он перебирается
- 5. Принцип Дирихле устанавливает связь между объектами и контейнерами при выполнении определённых условий. Принцип Дирихле
- 6. Принцип Дирихле Если в n клетках сидит m зайцев, причем m > n, то хотя бы
- 7. Принцип Дирихле
- 8. Принцип Дирихле Если в n клетках сидит m голубей, причем m то хотя бы в одна
- 9. Обобщенный принцип Дирихле Предположим, m зайцев рассажены в n клетках. Тогда если m > n, то
- 10. В классе 15 учеников. Докажите, что найдутся как минимум 2 ученика, отмечающих дни рождения в один
- 11. В ковре размером 3х3 метра Коля проделал 8 дырок. Докажите, что из него можно вырезать коврик
- 12. В 3А классе учится 27 школьников, знающих всего 109 стихотворений. Докажите, что найдется школьник, знающий не
- 13. В городе 15 школ. В них обучается 6015 школьников. В концертном зале городского Дворца культуры 400
- 14. В школе 5 восьмых классов: 8А, …, 8Д. В каждом из них учится по 32 человека.
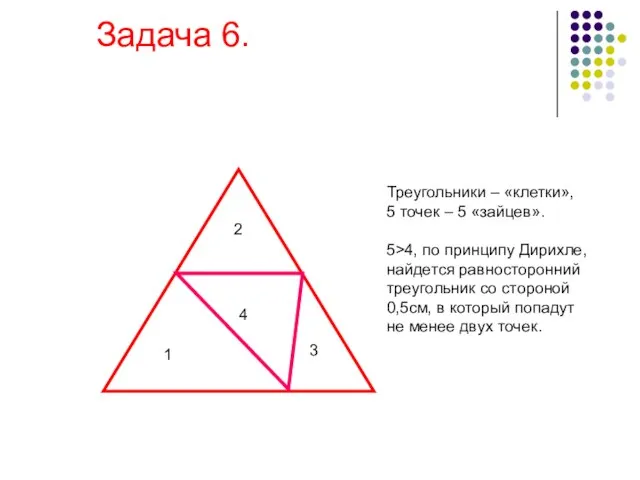
- 15. Внутри равностороннего треугольника со стороной 1см расположено 5 точек. Докажите, что расстояние между некоторыми двумя из
- 16. Задача 6. 2 1 4 3 Треугольники – «клетки», 5 точек – 5 «зайцев». 5>4, по
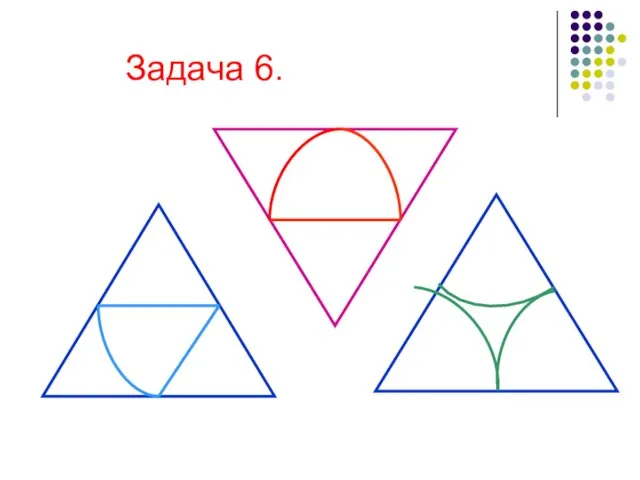
- 17. Задача 6.
- 18. Выводы: Таким образом, применяя данный метод, надо: Определить, что удобно в задаче принять за «клетки», а
- 19. С п а с и б о за внимание!
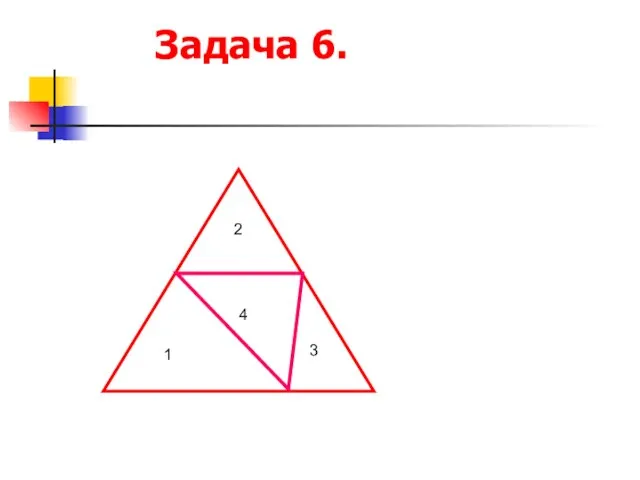
- 21. Задача 6. 2 1 4 3
- 23. Скачать презентацию

















 Презентация на тему "Обеспечение недопущения психологической перегрузки" - скачать презентации по Педагогике
Презентация на тему "Обеспечение недопущения психологической перегрузки" - скачать презентации по Педагогике Открытки (3)
Открытки (3) Galante-Series-Cover-Revamp
Galante-Series-Cover-Revamp Делители и кратные
Делители и кратные Истина-тайна, всегда тайна. А. Платонов
Истина-тайна, всегда тайна. А. Платонов В гостях у Барбариков
В гостях у Барбариков ОС "Школа 2100": содержание дошкольного образования
ОС "Школа 2100": содержание дошкольного образования Ковчег
Ковчег Уход за одеждой из шерстяных и шелковых тканей
Уход за одеждой из шерстяных и шелковых тканей Презентация на тему Рынок мяса в России: текущая ситуация и перспективы
Презентация на тему Рынок мяса в России: текущая ситуация и перспективы  давл тв тел
давл тв тел Фаэтон
Фаэтон Избирательный процесс
Избирательный процесс «Вопросы финансирования и практические аспекты реализации инвестиционных проектов »
«Вопросы финансирования и практические аспекты реализации инвестиционных проектов » Герои Отечественной войны 1812 года – наши земляки
Герои Отечественной войны 1812 года – наши земляки Фотоотчёт куратора группы ЭПМ 314
Фотоотчёт куратора группы ЭПМ 314 Палитра Место, где зарабатывают
Палитра Место, где зарабатывают Экологизация школьного курса окружающего мира
Экологизация школьного курса окружающего мира Мы и наша работа
Мы и наша работа От пера к компьютеру
От пера к компьютеру ОЗОН В АТМОСФЕРЕ
ОЗОН В АТМОСФЕРЕ Организация питанияв МОУ НОШ № 27
Организация питанияв МОУ НОШ № 27 Лекция_1,2_Методология_определение_и_предмет
Лекция_1,2_Методология_определение_и_предмет Бионика
Бионика План застройки г. Бежецк, развитие общественного центра
План застройки г. Бежецк, развитие общественного центра Комфортабельные автобусы
Комфортабельные автобусы Азбука ухода за морскими свинками
Азбука ухода за морскими свинками Особенности деятельности учителя начальных классов в условиях ФГОС
Особенности деятельности учителя начальных классов в условиях ФГОС