Содержание
- 2. Корпускулярно – волновой дуализм для излучения Частица света: фотон – в области видимого света (термин Гильберта
- 3. Фазовая и групповая скорости волн Волна: – фазовая скорость. – размерность скорости где λ – длина
- 4. Принцип корпускулярно – волнового дуализма Луи де Бройля Луи де Бройль распространил принцип корпускулярно – волнового
- 5. Математическая реализация гипотезы де Бройля Необходимо непротиворечивым образом каждой частице сопоставить колебатель-ный процесс. Природа этого колебательного
- 6. Математическая реализация гипотезы де Бройля: фазовая и групповая скорости. Эквивалентность колебательных процессов означает, что: Положим n=0.
- 7. Длина волны де Бройля Импульс релятивисткой частицы Покажем, что с точки зрения волн де Бройля, его
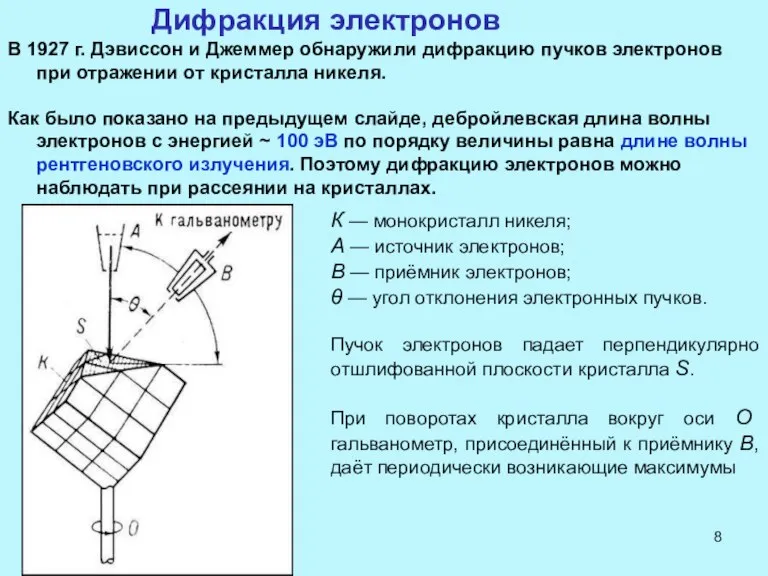
- 8. Дифракция электронов В 1927 г. Дэвиссон и Джеммер обнаружили дифракцию пучков электронов при отражении от кристалла
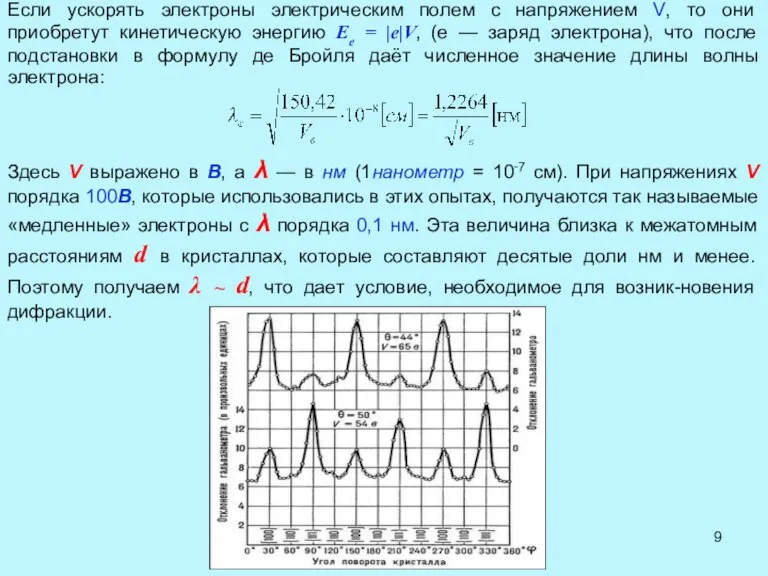
- 9. Если ускорять электроны электрическим полем с напряжением V, то они приобретут кинетическую энергию Ee = |e|V,
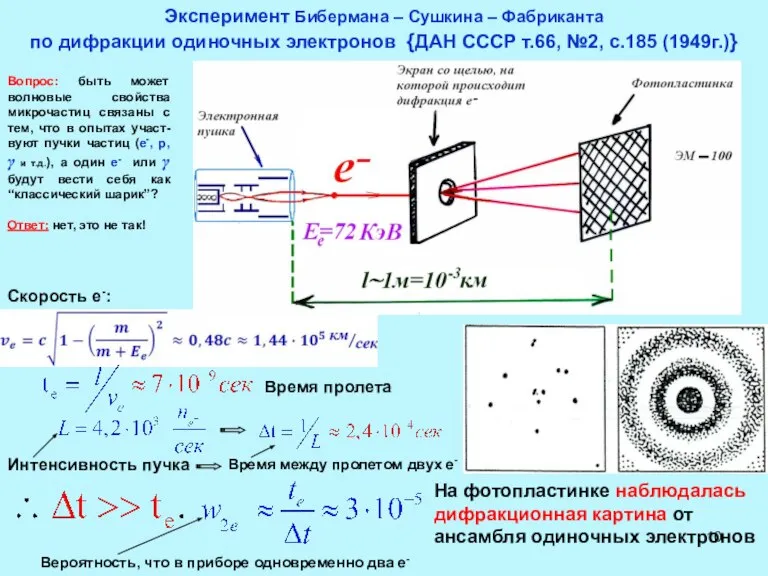
- 10. Эксперимент Бибермана – Сушкина – Фабриканта по дифракции одиночных электронов {ДАН СССР т.66, №2, с.185 (1949г.)}
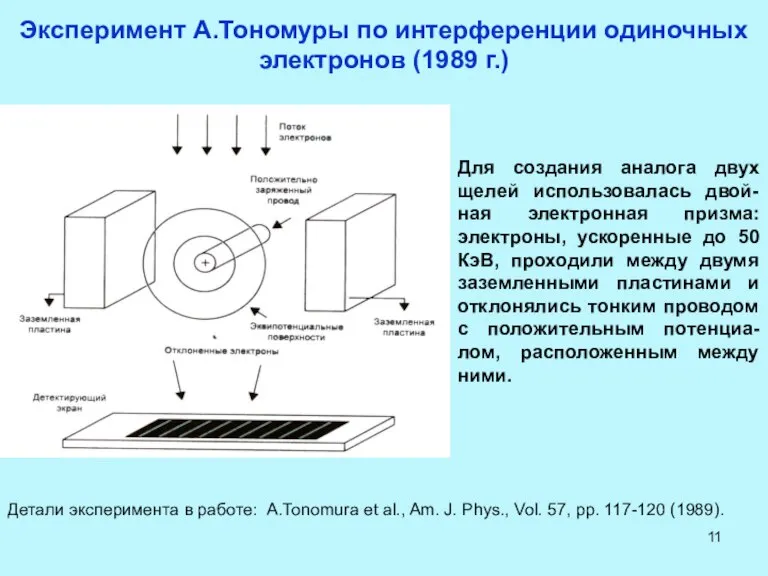
- 11. Эксперимент А.Тономуры по интерференции одиночных электронов (1989 г.) Для создания аналога двух щелей использовалась двой-ная электронная
- 12. Результат эксперимента А. Тономуры Каждая точка обозначает попадание электрона в детектирующий экран. а) 10 электронов; б)
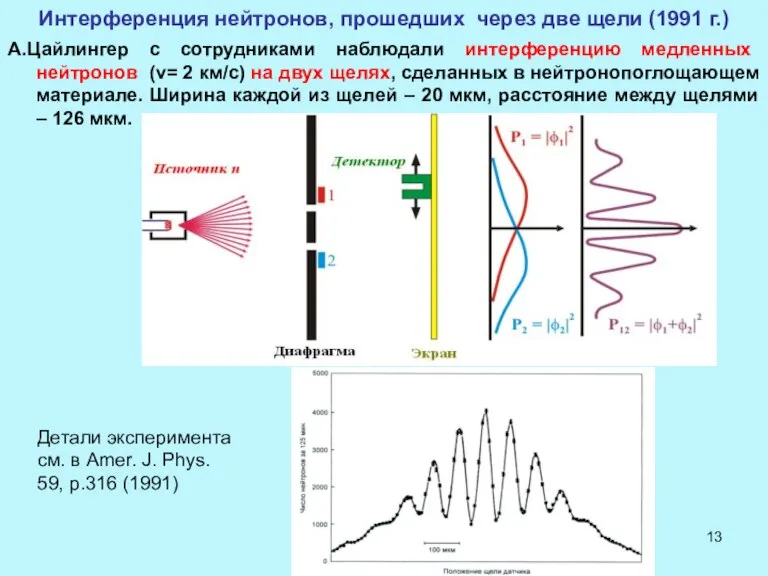
- 13. Интерференция нейтронов, прошедших через две щели (1991 г.) А.Цайлингер с сотрудниками наблюдали интерференцию медленных нейтронов (v=
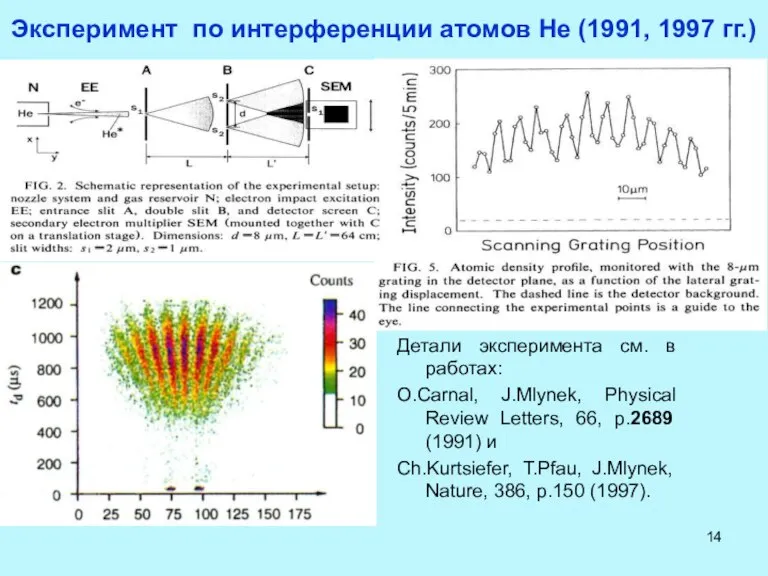
- 14. Эксперимент по интерференции атомов He (1991, 1997 гг.) Детали эксперимента см. в работах: O.Carnal, J.Mlynek, Physical
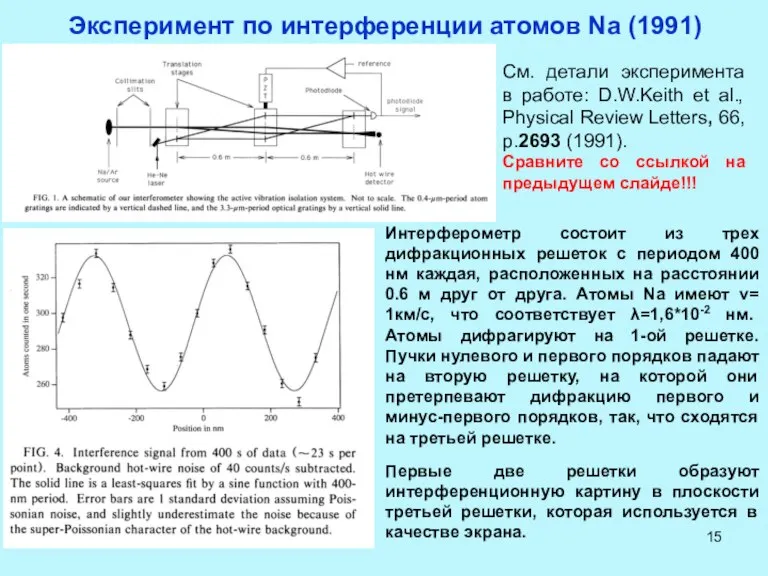
- 15. Эксперимент по интерференции атомов Na (1991) Интерферометр состоит из трех дифракционных решеток с периодом 400 нм
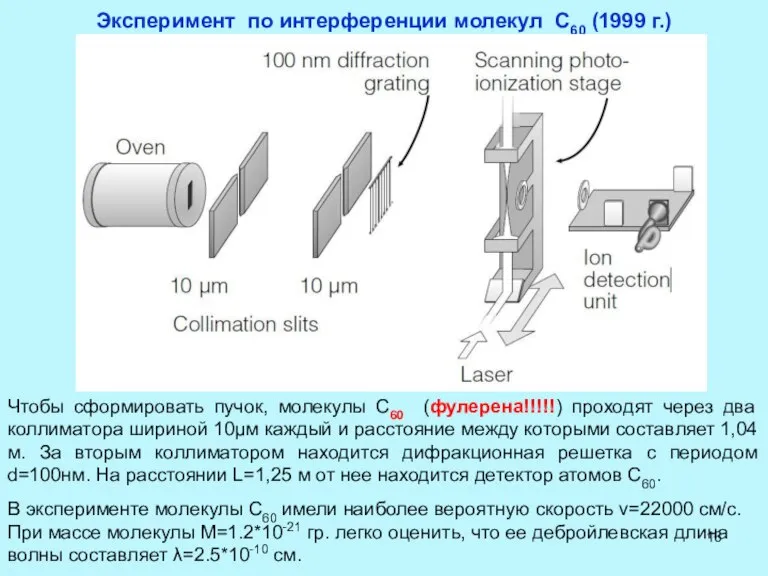
- 16. Эксперимент по интерференции молекул С60 (1999 г.) Чтобы сформировать пучок, молекулы С60 (фулерена!!!!!) проходят через два
- 18. Скачать презентацию







 Примерный эскиз баннера. Kronomir
Примерный эскиз баннера. Kronomir Глава 3. Экономика фирмы
Глава 3. Экономика фирмы Гончарова Ирина Алексеевна
Гончарова Ирина Алексеевна Оценка стоимости бренда
Оценка стоимости бренда Латинская Америка
Латинская Америка Психологическая служба школы«Ни себя, нм других нельзя изучать иначе как в деятельности и общении. Нельзя изучать человека холод
Психологическая служба школы«Ни себя, нм других нельзя изучать иначе как в деятельности и общении. Нельзя изучать человека холод Необычные факты о птицах
Необычные факты о птицах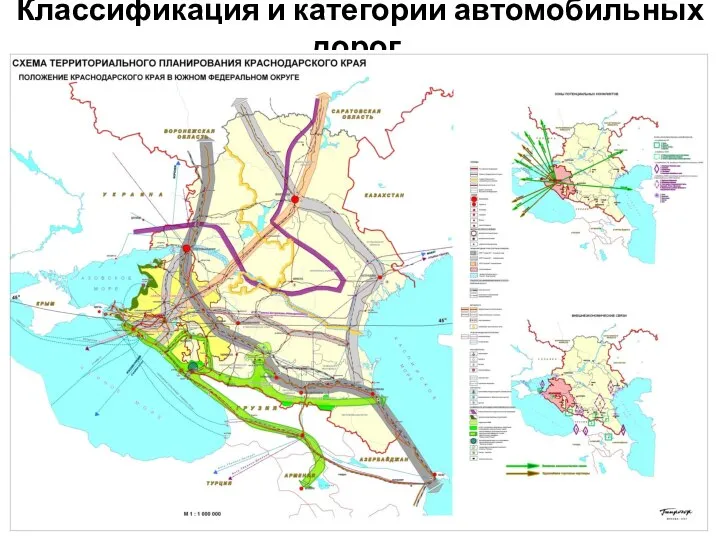 Классификация и категории автомобильных дорог
Классификация и категории автомобильных дорог Этикет 4 класс
Этикет 4 класс Влияние вредных привычек на сердечно-сосудистую и дыхательную системы
Влияние вредных привычек на сердечно-сосудистую и дыхательную системы Воля. Виды и содержания волевых процессов
Воля. Виды и содержания волевых процессов Э-74 Против курения
Э-74 Против курения Агентство по ипотечному жилищному кредитованию
Агентство по ипотечному жилищному кредитованию Возрождение Руси. Иван Калита
Возрождение Руси. Иван Калита Растительные сообщества и взаимосвязи в них
Растительные сообщества и взаимосвязи в них Чтение слов и предложений с буквой Ц
Чтение слов и предложений с буквой Ц Презентация на тему Древние германцы и Римская империя
Презентация на тему Древние германцы и Римская империя  Системный анализ предметной области кандидатской диссертации
Системный анализ предметной области кандидатской диссертации School subjects
School subjects Архимедова сила (7 класс)
Архимедова сила (7 класс) Здравствуй, милая картошка!
Здравствуй, милая картошка! Три среды обитания. Наземно-воздушная среда
Три среды обитания. Наземно-воздушная среда Формованный эластичный ППУ для автомобильной промышленности
Формованный эластичный ППУ для автомобильной промышленности Расшифровка моделей Indesit
Расшифровка моделей Indesit Выполнение эскиза в точечной технике
Выполнение эскиза в точечной технике Особенности питания студентов
Особенности питания студентов Портфолио педагога
Портфолио педагога Воспитательные традиции в системе дополнительного образования
Воспитательные традиции в системе дополнительного образования