Проблема поиска корней многочленов

Содержание
1. Введение
2. Определение многочлена
3. . Нахождение корней многочленов
4. Теорема Безу
5. Схема Горнера
6. Заключение
7. Список литературы

Введение
Изучению темы «Многочлены» в программе по математике основной школы уделяется большое внимание.
За пределами школьного курса остаются некоторые методы отыскания корней многочленов, операции деления многочлена на многочлен. В связи с этим школьники лишены возможности решить некоторые алгебраические уравнения высших степеней (в том числе возвратные, однородные), приемы решения которых тесно связаны с отысканием корней многочленов. Между
тем, такие задания встречаются в экзаменационных работах.
Поэтому целью моей работы стало нахождение формул и методов решения уравнений высших степеней, нахождение корней которых связано с отысканием корней многочленов.
Меню

Определение многочлена
В школьной алгебре одночленом от некоторой буквы x называется алгебраическое выражение вида ахm, где a - некоторое число, x - буква, m - целое неотрицательное число. Одночлен ax0 отождествляется с числом a, так что числа рассматриваются как одночлены. Подобные одночлены складываются по правилу
axm + bxm = (a+b)xm, называемому приведением подобных членов. Многочленом или полиномом называется алгебраическая сумма одночленов. Поэтому любой полином можно записать в канонической форме a0xn + a1xn-1 + …+ an, с расположением членов в порядке убывания показателей.
Меню

Нахождение корней многочлена
1. В общем случае решение квадратных уравнений сводится к нахождению дискриминанта:
Формула дискриминанта: D = b2 – 4ac
В общем случае корни уравнения равны: x1,2 = -b±√D/2a
Очевидно, в случае с нулевым дискриминантом, оба корня равны x1,2 = -b/2a
Например: x2 + 3x – 4 = 0
Ответ: 1, 4
Меню

2. Теорема Виета:
Приведенным квадратным уравнением называется уравнение с единичным коэффициентом при старшем члене: х² + рх+q = 0.
В этом случае целесообразно применять теорему Виета, которая позволяет получить относительно корней уравнения следующую систему уравнений :
x1 + x2 = -р
x1 ∙ x2 = q
Например: x2 – 5x + 6 = 0
2 · 3 = 6
2 + 3 =5
Ответ: 2,3
Франсуа́ Вие́т (1540 — 13 февраля 1603) — французский математик, основоположник символической алгебры. По образованию и основной профессии — юрист.
Меню

3. Вынесение общего множителя за скобки:
Это преобразование является непосредственным следствием распределительного закона ac + bc = c(a + b).
Пример: решить уравнение 12 y3 – 20 y2 = 0.
Решение. Имеем: 12 y3 – 20 y2 = 4 y2 · 3y – 4 y2 · 5 = 4 y2 (3 y – 5),
тогда 4 y2 (3 y – 5) = 0,
отсюда 4 y2 = 0 или (3 y – 5) = 0; у=0 или у=5/3.
Ответ: у = 0 и у = 5/3.
4. Способ группировки:
Этот способ заключается в том, что слагаемые многочлена можно сгруппировать различными способами на основе сочетательного и переместительного законов. Общий множитель можно вынести за скобку и исходный многочлен окажется представленным в виде произведения.
Пример: х3 – 8х2 + 3х – 24 = 0,
( х3 +3х) −(8х²+24) = 0,
x(x2+3) - 8(х2+3) =0,
(x-8) (х2+3) =0,
х=8 или (х2+3)≠0. Ответ: 8
Меню

5. Использование формул сокращенного умножения:
Пример. Разложить на множители многочлен x4 – 1.
Решение. Имеем: x4 – 1 = ( x2 )2 – 1 = ( x2 – 1)( x2 + 1) = ( x2 – 1 )( x2 + 1) =
( x + 1)( x – 1)( x2 + 1). ( x + 1)( x – 1)( x2 + 1)=0,
отсюда х = -1, х = 1, ( x2 + 1)≠0.
Ответ: 1, -1.
Меню

6. Метод введения новой переменной:
Пример. Решить уравнение х(х-1)(х-2)(х-3) = 24. Решение. Заметив, что х(х-3) = х2 – 3х, а
(х-1)(х-2) = х2 – 3х + 2, перепишем уравнение в виде
(х2 – 3х)(х2 – 3х + 2) = 24.
Введя новую переменную у = х2 – 3х, преобразуем уравнение к виду у(у+2) = 24 и, далее, у2 + 2у – 24 = 0.
Корнями этого квадратного уравнения служат числа
4 и -6.
Возвращаясь к переменной х, мы должны решить два уравнения:
х2 – 3х = 4; х2 – 3х = −6.
Из первого уравнения находим х1 = 4, х2 = −1; второе уравнение не имеет действительных корней.
Ответ: 4; -1.
Меню

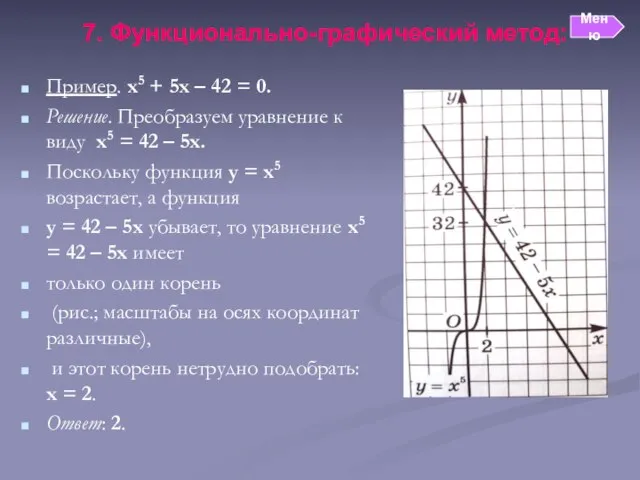
7. Функционально-графический метод:
Пример. х5 + 5х – 42 = 0.
Решение. Преобразуем уравнение к виду х5 = 42 – 5х.
Поскольку функция у = х5 возрастает, а функция
у = 42 – 5х убывает, то уравнение х5 = 42 – 5х имеет
только один корень
(рис.; масштабы на осях координат различные),
и этот корень нетрудно подобрать: х = 2.
Ответ: 2.
Меню

Теорема Безу
Теорема: При делении многочлена n-й степени относительно x на двучлен (x-a) остаток равен значению делимого при x=a.
(Буква a может обозначать любое действительное или мнимое число, т.е. любое комплексное число.)
При решении уравнений с помощью теоремы Безу необходимо:
Найти все целые делители свободного члена;
Из этих делителей найти хотя бы один корень уравнения (а);
Левую часть уравнения разделить на (х-а);
Записать в левой части уравнения произведение делителя и частного;
Решить полученное уравнение.
Этье́нн Безу́ (31 марта 1730, Немур — - 27 сентября 1783, Бас-Лож близ Фонтенбло) — французский математик, член Парижской академии наук (1758).
Меню

Пример: Найти корни уравнения x4+4x2–5 = 0.
Среди делителей свободного члена число 1 является корнем данного уравнения, а это значит, что по следствию 2 из теоремы Безу многочлен x4+4x2–5 делится на (x–1) без остатка:
значит x4+4x2–5 =(x–1)(x3+x2+5x+5).
Среди делителей свободного члена многочлена x3+x2+5x+5,
x=-1 является его корнем, а это значит, что по следствию 2 из теоремы Безу x3+x2+5x+5 делится на (x+1) без остатка:
значит x3+x2+5x+5 =(x+1)(x2+5).
Отсюда x4+4x2–5 =(x–1)(x+1)(x2+5).
(x2+5) на множители не раскладывается, т.к. действительных корней не имеет, поэтому
(x–1)(x+1)(x²+5)=0
(x–1)=0 или (x+1)=0 или (x2+5)=0
х = 1 х = -1 х² ≠ -5
Ответ: 1; -1.

Схема Горнера
Горнер Джордж Уильямс (11 октября 1821 — 1905) - английский математик, работал в области алгебры. В 1819 опубликовал способ приближенного вычисления вещественных корней многочлена, который назвал способом Руффини — Горнера. Этот способ был известен китайцам еще в 13 в. Именем Горнера названа схема деления многочлена на двучлен (х — а).
Пусть р(х) = bх4 + сх3 +dx2 + ех + f. Разделив р(х) на х – а, получим
р(х) = (х - а)q(x) + r, где q(x) – некоторый многочлен третьей степени, коэффициенты которого нам пока неизвестны: q(x) = kx3 + mx2 + nx + s. Итак,
bх4 + сх3 +dx2 + ех + f = (kx3 + mx2 + nx + s)(х - а) + r. (1)
Раскрыв скобки в правой части тождества (1), получим:
bх4 + сх3 +dx2 + ех + f = kx4 + ( m – ka)x3 + (n – ma)x2 + (s – na)x + r – sa. Неопределенные коэффициенты k, m, n, s, r связаны с известными коэффициентами a, b, c, d, e, f следующими соотношениями:
Меню

Пример. Найти корни уравнения х3 + 4х2 + х – 6 = 0.
Решение: Находим делители свободного члена ±1; ± 2; ± 3; ± 6.
Здесь, а = 1 (х - 1 = х – а), а коэффициенты многочлена-делимого равны соответственно 1, 4, 1, -6. Строим таблицу для применения схемы Горнера:
Итак, коэффициенты частного – числа 1, 5, 6, а остаток r = 0.
Значит, х3 + 4х2 + х – 6 = (х – 1) (х2 + 5х + 6) = 0.
Отсюда: х – 1 = 0 или х2 + 5х + 6 = 0,
х = 1 х 1 = -2; х2 = -3.
Ответ: 1, -2, -3.

Заключение
Теорема Безу находит применение при рассмотрении одной из важнейших задач математики – решении уравнений.
Схема Горнера же удобна тем, что при ее применении нужно использовать меньшее, чем при делении многочлена на многочлен «уголком», число арифметических операций, и вообще она более компактна.
Данный материал можно использовать, на элективных курсах, на дополнительных занятиях при подготовке учащихся к ЕГЭ.
Меню